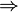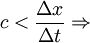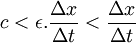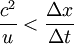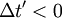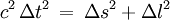Intervalle d'espace-temps - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Expression en relativité restreinte - Relation entre événements - Invariance - Le cône de lumière - Ordre temporel et genre - Cas de l'invariance comme hypothèse - Métrique

Le cône de lumière

Le cône de lumière de l'événement A définit une partition de l'espace-temps permettant en particulier de distinguer le passé du futur de façon absolue

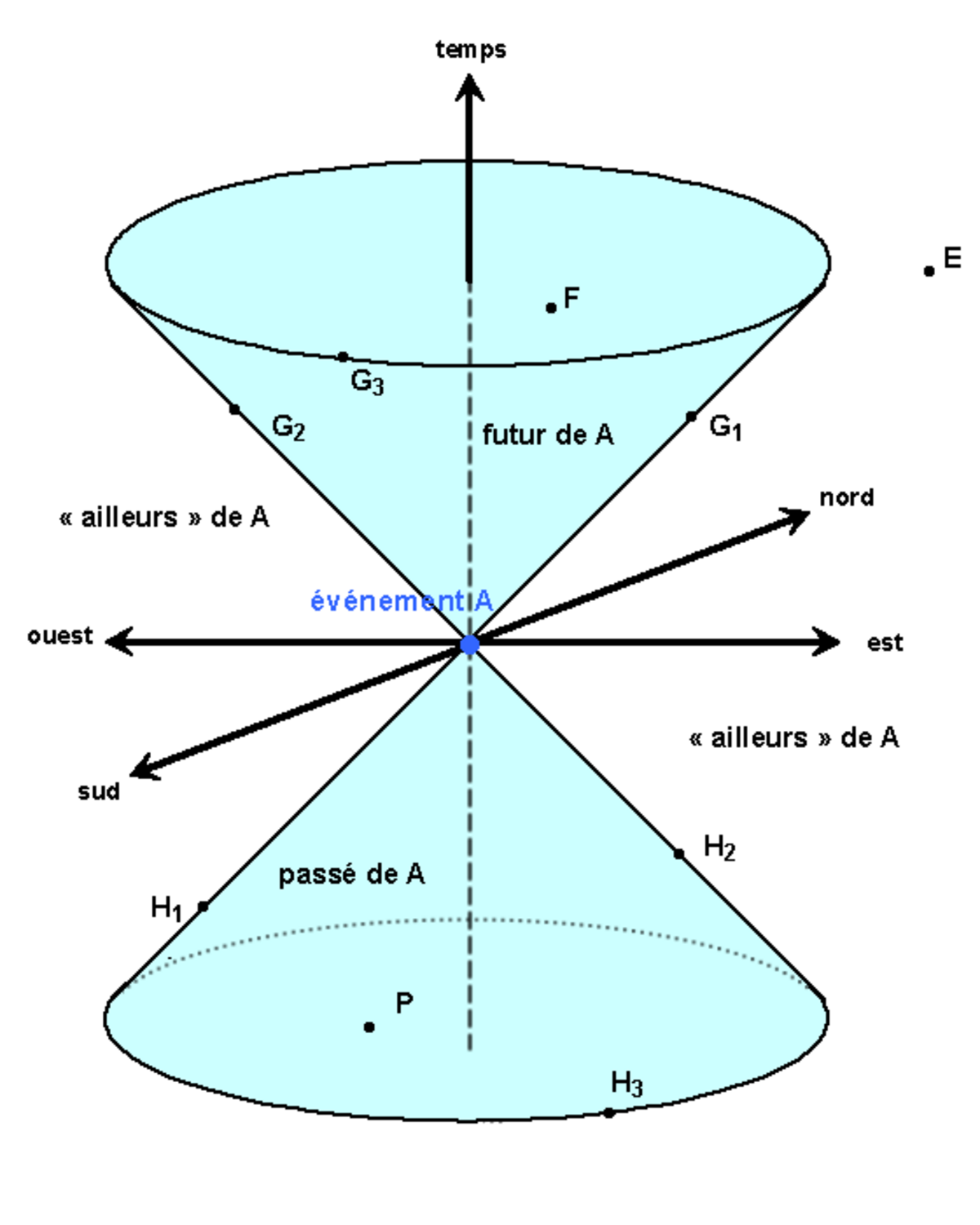
Si on se fixe un événement O particulier comme objet d'étude, on peut partager l'espace-temps en régions regroupant les événements qui sont séparés de O par un intervalle d'espace-temps de genre temps, ceux qui sont séparés de O par un genre lumière et ceux qui sont séparés de O par un genre espace. Cette partition de l'espace-temps à quatre dimensions se fait sous la forme d'un cône à trois dimensions : l'intérieur correspond au premier cas, le bord au deuxième et l'extérieur au troisième. Ces régions correspondent aux différentes possibilités de lien causal avec l'événement O.

Bien entendu, chaque événement possède son propre cône de lumière.

La difficulté de représentation tient en ce que quatre coordonnées, une de temps et trois d'espace, sont nécessaires pour caractériser un événement et qu'il est impossible de figurer un point à quatre coordonnées dans notre espace à trois dimensions. Pour le graphique, on reduit donc le nombre de dimensions spatiales à 2.

Ordre temporel et genre

Diagramme de Minkowski représentant l'inversion temporelle apparente des évènements A et B pour l'observateur O et O'. Pour O, B a lieu avant A, tandis que pour O', en mouvement rapide par rapport à O, c'est A qui se produit avant B.

Par principe, les changements de référentiels physiquement réalistes respectent l'orientation de l'axe du temps : on suppose donc que vues d'un référentiel ou d'un autre les aiguilles d'une montre ne changent pas leur sens de rotation, que si une pomme chute de sa branche vu de l'un, alors elle n'y remonte pas vu depuis un autre.

Par contre, dans certains cas l'ordre temporel observé entre deux évènements peut changer d'un référentiel à l'autre : si les deux évènements sont séparés par un intervalle de genre espace, leur ordre temporel observé peut changer d'un référentiel à l'autre, et il y a aussi des référentiels pour lesquels les deux évènements sont simultanés. S'ils sont séparés par un intervalle de genre temps, tous les observateurs constatent le même ordre (mais avec des écarts temporels différents).

« L'invariance par changement de référentiel de l'ordre temporel entre deux événements séparés par un intervalle de genre temps » est en équivalence tautologique avec le principe de non-inversion de l'axe du temps par changement de référentiel.

Mais on peut vouloir se convaincre, par quelques considérations mathématiques, que cette invariance est bien une conséquence de ce principe :

Les seuls changements de référentiel que la physique permette respectent l'orientation de l'axe du temps et l'orientation des repères tridimensionnels (l'orientation unanimement admise étant celle de la main droite), ce sont aussi les changements continus à partir du référentiel initial, et sont appelés transformations propres et orthochrones.

Considérons un couple d'événements du genre temps tel que l'intervalle Δt de A vers F soit positif (t(F) est plus grand que t(A), ou F est postérieur à A). Pour que cet intervalle change de signe (F devenant antérieur à A) il faudrait qu'il traverse la valeur nulle, ce qui est impossible. En effet le carré Δt²de l'intervalle temporel est égal à la somme de deux carrés selon la formule

où le premier terme du second membre est strictement positif (et invariant par changement de référentiel) et le second terme, carré d'une distance euclidienne, est positif ou nul. Par conséquent ce carré Δt² ne peut pas s'annuler. Il en est de même de l'intervalle temporel Δt lui-même, lequel, ne pouvant pas s'annuler, ne peut pas changer continûment de signe. Ainsi, si A précède F pour un certain observateur, il en sera toujours de même pour tout observateur physiquement admissible. Si A était antérieur à F, F ne peut pas agir sur A en devenant lui-même antérieur à A.

Étant donné deux événements A et B tels que dans le référentiel $(R)$ de l'observateur $Δ t = t B - t A > 0$ , et en supposant $Δ x = x B - x A > 0$ avec un bon choix de l'axe x.

Considérons un référentiel $(R')$ en translation par rapport au repère (R), à la vitesse le long de l'axe des x, avec $0 < u < c$ .

D'après les transformations de Lorentz, la durée entre les deux événements, vue du référentiel $(R')$ vaut :
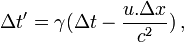
$\Delta t'=\gamma(\Delta t-\frac{u.\Delta x}{c^2})\, ,$ avec : $\, \gamma= \left( 1 - u^2/c^2 \right)^{-1/2} > 0$ .
$Δ t$ étant positif, que dire du cas $Δ t'$ négatif ?
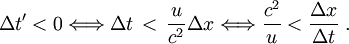
$\Delta t'<0 \Longleftrightarrow \Delta t\,<\,\frac{u}{c^2}\Delta x \Longleftrightarrow \frac{c^2}{u}<\frac{\Delta x}{\Delta t}\;.$
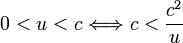
Or $0<u<c \Longleftrightarrow c< \frac{c^2}{u}$
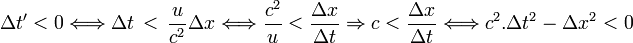
D'où : $\Delta t'<0 \Longleftrightarrow \Delta t\,<\,\frac{u}{c^2}\Delta x \Longleftrightarrow \frac{c^2}{u}<\frac{\Delta x}{\Delta t} \Rightarrow c<\frac{\Delta x}{\Delta t} \Longleftrightarrow c^2.\Delta t^2-\Delta x^2<0$ , d'où les deux événements sont séparés par un intervalle de genre espace.
Une flèche à sens unique $\Rightarrow$ bloque la réciproque, mais on a : $c<\frac{\Delta x}{\Delta t} \Rightarrow$ il existe un nombre positif $ε < 1$ tel que $c<\epsilon . \frac{\Delta x}{\Delta t}<\frac{\Delta x}{\Delta t}$ . En posant $\ u=c.\epsilon < c$ , on obtient $\frac{c^2}{u}<\frac{\Delta x}{\Delta t}$ et on peut toujours construire un référentiel $(R')$ en translation à la vitesse pour lequel $\ \Delta t'<0$ .