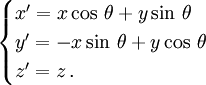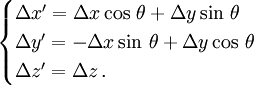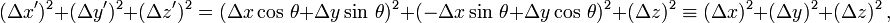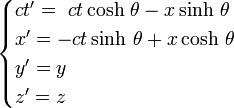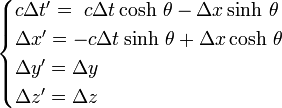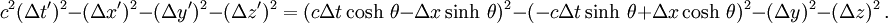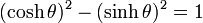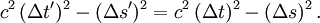Intervalle d'espace-temps - Définition

Les deux axiomes sont : le principe de relativité et l'invariance de la vitesse de la lumière par changement de référentiel (inertiel, comme tous les référentiels considérés ici).

• Si, dans un certain référentiel, deux événements sont séparés de la distance spatiale et de la distance temporelle de telle sorte que la vitesse de la lumière, alors on a : .

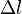
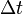
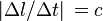
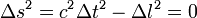
Si les deux mêmes événements sont vus depuis un autre référentiel, alors les distances spatiale et temporelle y sont et , avec la vitesse de la lumière, qui a la même valeur dans cet autre référentiel, d'après le deuxième axiome. On en déduit que dans ce référentiel aussi, on a

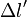
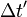
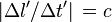
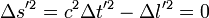
Ainsi, si dans un référentiel, il en est de même dans tout autre.

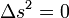
• Dans chaque référentiel et pour tout couple d'événements suffisamment proches, et sont des infiniment petits du même ordre de grandeur car les changements de référentiels sont des fonctions affines à coefficients constants, donc les relations entre les , d'un référentiel à l'autre sont linéaires ou affines. et s'annulent simultanément, donc il existe un nombre a tel que . Ce nombre ne peut pas dépendre de la position relative des deux référentiels car l'espace-temps est supposé homogène, donc il ne dépend que de la vitesse relative des deux référentiels. Mais il ne peut pas dépendre de la direction de cette vitesse car l'espace-temps est supposé isotrope. Ainsi il ne dépend que de la valeur absolue de la vitesse relative, ou encore de son carré : .
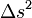
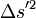
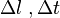
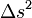
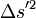
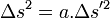
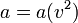
• Considérant trois référentiels, le principe de relativité imposant que les lois y soient les mêmes, on a : et . Ainsi . Or dépend de l'angle entre et , angle n'intervenant pas dans a(v²).a(v'²). Donc, est un nombre constant, ne dépendant pas de la vitesse relative des référentiels.
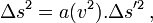
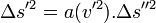
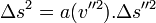
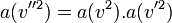
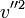
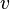
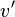
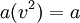
• Comme , on a .

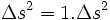
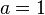
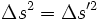
On ramene le problème à deux dimensions pour plus de lisibilité, donc on néglige les détails sur les rotations spatiales.

En considérant deux référentiels et en translation rectiligne uniforme l'un par rapport à l'autre à la vitesse , les transformations de Lorentz utilisées sont :

avec et ,

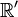
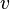
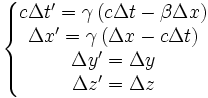
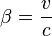
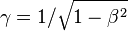
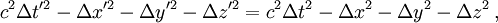
Le calcul suivant illustre le rapport étroit entre les formules de transformations de Lorentz et l'invariance du carré de l'intervalle spatio-temporel et la possibilité de passer d'un formalisme à l'autre.

En géométrie euclidienne, une rotation d'angle θ du système de coordonnées autour de l'axe Oz laisse invariante la distance entre deux points. Les formules de changement d'axes de coordonnées correspondant à cette rotation et donnant les nouvelles coordonnées en fonction des anciennes s'écrivent :

Par conséquent les différences de coordonnées entre les deux points A et B deviennent

On en déduit

formule montrant bien l'invariance de cette somme des carrés.

En relativité restreinte les transformations de Lorentz permettent de passer du système « fixe » à un système animé d'une vitesse v le long de l'axe Ox. En utilisant le paramètre angulaire θ défini par

  soit  

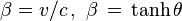
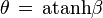
les formules de Lorentz s'écrivent comme des formules de rotation d'axes à ceci près que les fonctions trigonométriques sont remplacées par les fonctions hyperboliques. On a les expressions :

Par conséquent si on considère deux événements, les différences de coordonnées se transformeront comme

On en déduit :

Comme

on aboutit bien à la formule d'invariance annoncée