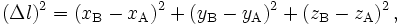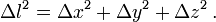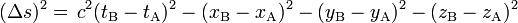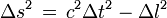Intervalle d'espace-temps - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Expression en relativité restreinte - Relation entre événements - Invariance - Le cône de lumière - Ordre temporel et genre - Cas de l'invariance comme hypothèse - Métrique

Introduction

Avant Einstein

Avec Einstein

En physique des particules

Méta

Le carré de l’intervalle d'espace-temps entre deux événements dans l'espace-temps de la relativité restreinte ou générale est l'équivalent du carré de la distance géométrique entre deux points dans l'espace euclidien. Cette quantité est invariante par changement de référentiel.

Quand le carré de l'intervalle d'espace-temps entre deux événements est positif ou nul (le terme carré n'est ici employé que de manière formelle), alors les deux événements peuvent être connectés par un lien de cause à effet, et l'intervalle d'espace-temps (défini en prenant la racine carrée) permet de définir le temps propre entre ces deux événements.

Quand le carré de l'intervalle d'espace-temps entre deux événements est strictement négatif, alors ils sont causalement indépendants l'un de l'autre, et l'intervalle d'espace temps n'est pas défini (ou au mieux comme étant un nombre imaginaire), mais en prenant la racine carrée de l'opposé du carré on obtient la distance propre entre ces événements.

Le carré de l'intervalle d'espace-temps sert de définition de la pseudo-métrique de l'espace de Minkowski en relativité restreinte, ainsi que de la pseudo-métrique infinitésimale dans l'espace courbe de la relativité générale.

Expression en relativité restreinte

Dans l'espace euclidien en trois dimensions, le carré de la distance $Δ l$ entre deux points A et B de coordonnées (x, y, z) et (x, y, z) par rapport à un repère cartésien orthonormé s'exprime sous la forme :

ce que l'on écrit couramment de façon plus condensée

Il est évident qu'en physique classique, cette grandeur est invariante par changement de référentiel. Mais ce n'est plus le cas en physique relativiste.

Dans la géométrie de l'espace-temps de la relativité restreinte, on écrit le « carré de l'intervalle d'espace-temps », noté $Δ s 2$ , entre deux événements A et B de coordonnées (t, x, y, z) et (t, x, y, z) dans un espace-temps à quatre dimensions (une de temps, soit t, et trois d'espace) sous la forme

expression dans laquelle le facteur c² s'impose par le biais des transformations de Lorentz ou des principes de la relativité restreinte, suivant la méthode utilisée pour justifier son invariance par changement de référentiel inertiel.

Alors que le carré de la distance géométrique euclidienne ne contenait que des signes « + » et se révélait donc toujours positif, l'expression de l'intervalle spatio-temporel contient un signe « - » et peut de ce fait être un nombre positif, négatif ou nul, selon la taille respective de la séparation spatiale Δl et du terme de séparation temporelle cΔt des deux événements. Il ne faut pas s'étonner que le carré $Δ s 2$ puisse se révéler négatif car cette écriture n'est que formelle et est faite pour souligner que « le carré de l'intervalle d'espace-temps » a la dimension du carré d'une distance. Par conséquent, la notion de « distance » (nous employons d'ailleurs ici le terme d'intervalle d'espace-temps) n'a plus la signification concrète qu'elle possédait en géométrie non relativiste.