Logique floue - Définition

Opérateurs flous

Les opérateurs flous (ou fuzzy) peuvent être implémentés de diverses manières et une même application peut d'ailleurs faire appel à des implémentations différentes judicieusement choisies selon le contexte.

L'exemple ci-dessous montre que, contrairement à une opinion parfois exprimée, le choix des opérateurs à utiliser n'est pas une simple question de goût ou d'inspiration du moment.

Exemple d'utilisation

Voici un exemple qui montre comment combiner des opérateurs flous (fuzzy) de divers types.

• l'exemple : confirmer l'appartenance d'une personne à un groupe

Une personne sera plus ou moins membre (à un niveau fzMembre, compris entre 0 et 1, inclusivement) d'un groupe, disons les flower lovers, soit si, pour n'importe quelle raison, elle en fait déjà plus ou moins partie (à un niveau fzDejaMembre), soit si elle a une assez bonne connaissance des orchidées (fzConnaitOrchidees) et que la connaissance des orchidées est un critère assez déterminant (fzOrchideesAmis) d'appartenance au groupe des flower lovers.

• une solution qui paraît bonne est :

      fzMembre = Zadeh_OR( fzDejaMembre, Multiply_AND( fzConnaitOrchidees, fzOrchideesAmis ))      

Zadeh OR

Multiply AND

• et s'implémente comme :

      fzMembre = max( fzDejaMembre, ( fzConnaitOrchidees * fzOrchideesAmis ))      

      pour fzDejaMembre=0 (faux), fzConnaitOrchidees=0.778 et fzOrchideesAmis=0.9, on trouve 0.7      pour fzDejaMembre=0.7, fzConnaitOrchidees=0.8 et fzOrchideesAmis=0.9, on trouve 0.72      pour fzDejaMembre=0.72, fzConnaitOrchidees=0.8 et fzOrchideesAmis=0.9, on retrouve 0.72      pour fzDejaMembre=0.72, fzConnaitOrchidees=0.5 et fzOrchideesAmis=0.9, on conserve 0.72      (ce qui est le résultat vraisemblablement attendu)      

Autres solutions

• une solution qui n'utiliserait que les opérateurs de Zadeh serait :

      fzMembre = Zadeh_OR( fzDejaMembre, Zadeh_AND( fzConnaitOrchidees, fzOrchideesAmis ))      

Zadeh OR

Zadeh AND

      fzMembre = max( fzDejaMembre, min( fzConnaitOrchidees, fzOrchideesAmis ))      

      pour fzDejaMembre=0 (faux), fzConnaitOrchidees=0.778 et fzOrchideesAmis=1 (vrai), on trouve 0.778      pour fzDejaMembre=0 (faux), fzConnaitOrchidees=0.778 et fzOrchideesAmis=0.9, on trouve aussi 0.778      (ce qui est trop élevé)      pour fzDejaMembre=0.778, fzConnaitOrchidees=0.8 et fzOrchideesAmis=0.9, on trouve 0.8      pour fzDejaMembre=0.8, fzConnaitOrchidees=0.8 et fzOrchideesAmis=0.9, on retrouve 0.8      pour fzDejaMembre=0.8, fzConnaitOrchidees=0.5 et fzOrchideesAmis=0.9, on conserve 0.8      (ce qui est stable mais trop élevé)      

• une solution qui n'utiliserait que les opérateurs représentables par des paraboloïdes hyperboliques serait :

      fzMembre = Add_OR( fzDejaMembre, Multiply_AND( fzConnaitOrchidees, fzOrchideesAmis ))      

Add OR

Multiply AND

      fzMembre = fzDejaMembre + (fzConnaitOrchidees*fzOrchideesAmis) - (fzDejaMembre*fzConnaitOrchidees*fzOrchideesAmis)      

      pour fzDejaMembre=0 (faux), fzConnaitOrchidees=0.778 et fzOrchideesAmis=0.9, on trouve 0.7      pour fzDejaMembre=0.7, fzConnaitOrchidees=0.8 et fzOrchideesAmis=0.9, on trouve 0.916      (ce qui est sûrement trop élevé)      pour fzDejaMembre=0.916, fzConnaitOrchidees=0.8 et fzOrchideesAmis=0.9, on trouve 0,97648      (ce qui est instable et sûrement beaucoup trop élevé)      pour fzDejaMembre=0,97648, fzConnaitOrchidees=0.5 et fzOrchideesAmis=0.9, on trouve 0. 987 064      (une augmentation bien malvenue)      

Convergence

Les trois méthodes exposées ci-dessus convergent lorsque les valeurs d'entrée sont booléennes

      pour fzDejaMembre=0 (faux), fzConnaitOrchidees=0 (faux) et fzOrchideesAmis=1 (vrai), on trouve 0 (faux)      pour fzDejaMembre=0 (faux), fzConnaitOrchidees=1 (vrai) et fzOrchideesAmis=1 (vrai), on trouve 1 (vrai)      pour fzDejaMembre=1 (vrai), fzConnaitOrchidees=1 (vrai) et fzOrchideesAmis=1 (vrai), on retrouve 1 (vrai)      pour fzDejaMembre=1 (vrai), fzConnaitOrchidees=0 (faux) et fzOrchideesAmis=1 (vrai), on conserve 1 (vrai)      

Opérateur implique

Pour l'exemple à l'orchidée ci-dessus, une situation normale est que la connaissance des orchidées implique l'appartenance au groupe. C’est-à-dire, plus précisément, qu'on ne peut pas connaître les orchidées et, simultanément, ne pas être membre du groupe des amis des fleurs.

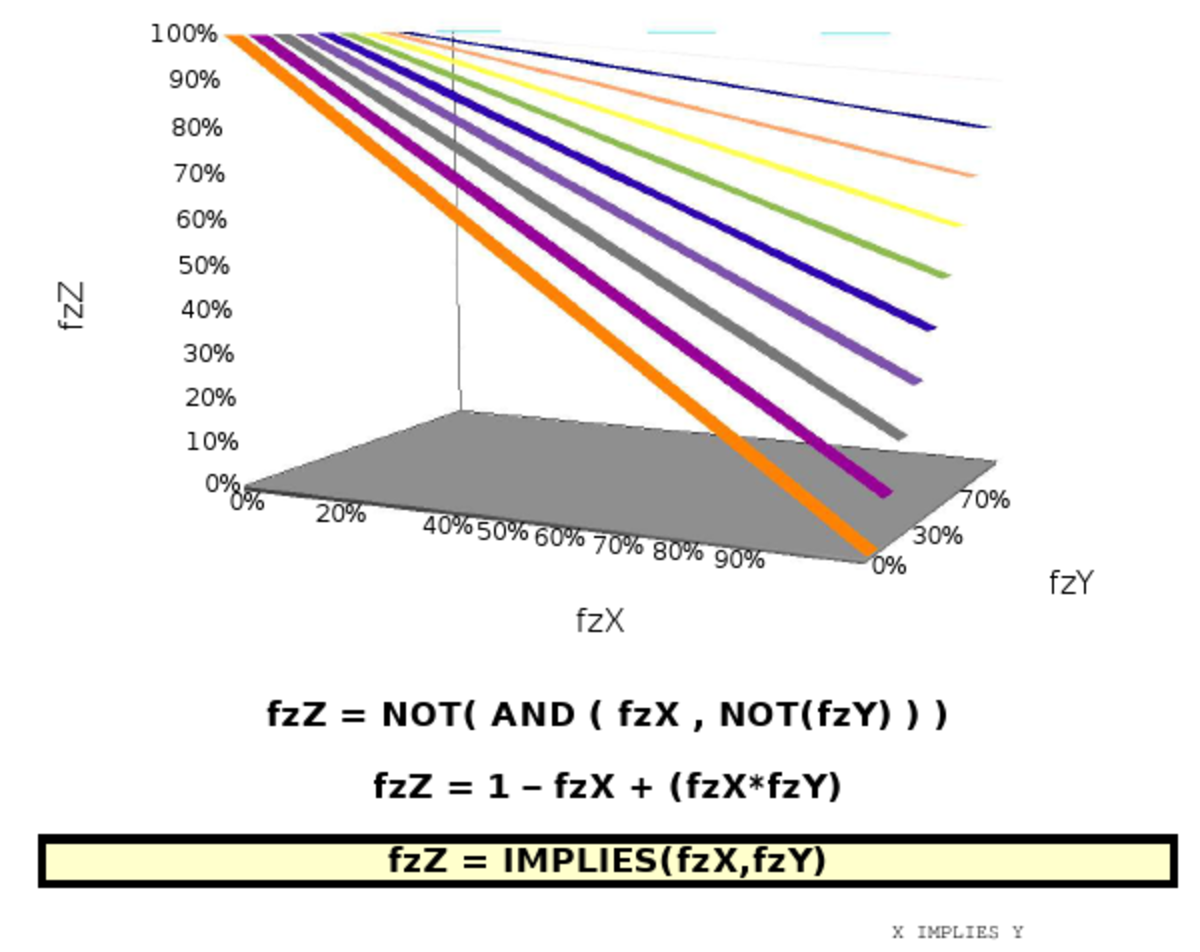
      fzImpliqueOk = NOT( AND( fzConnaitOrchidees, NOT( fzMembre ) ) )      

De même qu'on a vu ci-dessus plusieurs manières d'implémenter les opérateurs OR et AND, il y a aussi plusieurs manières d'implémenter la notion d'implication.

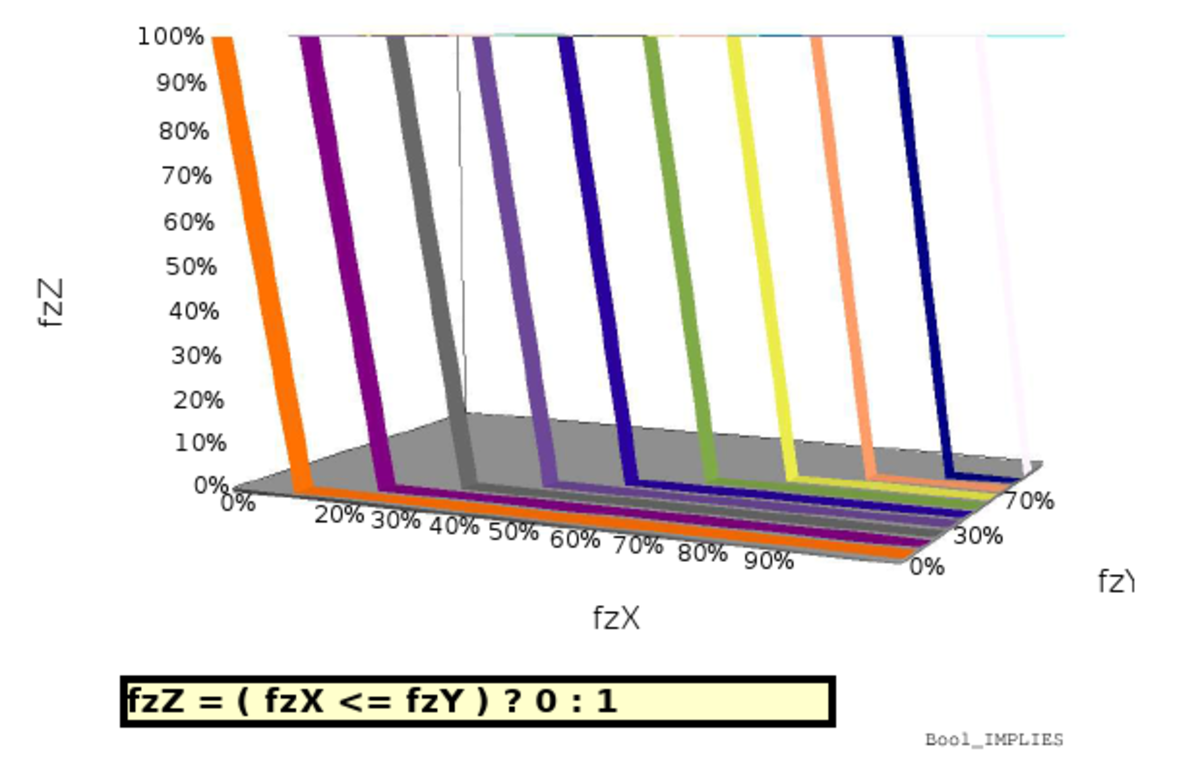
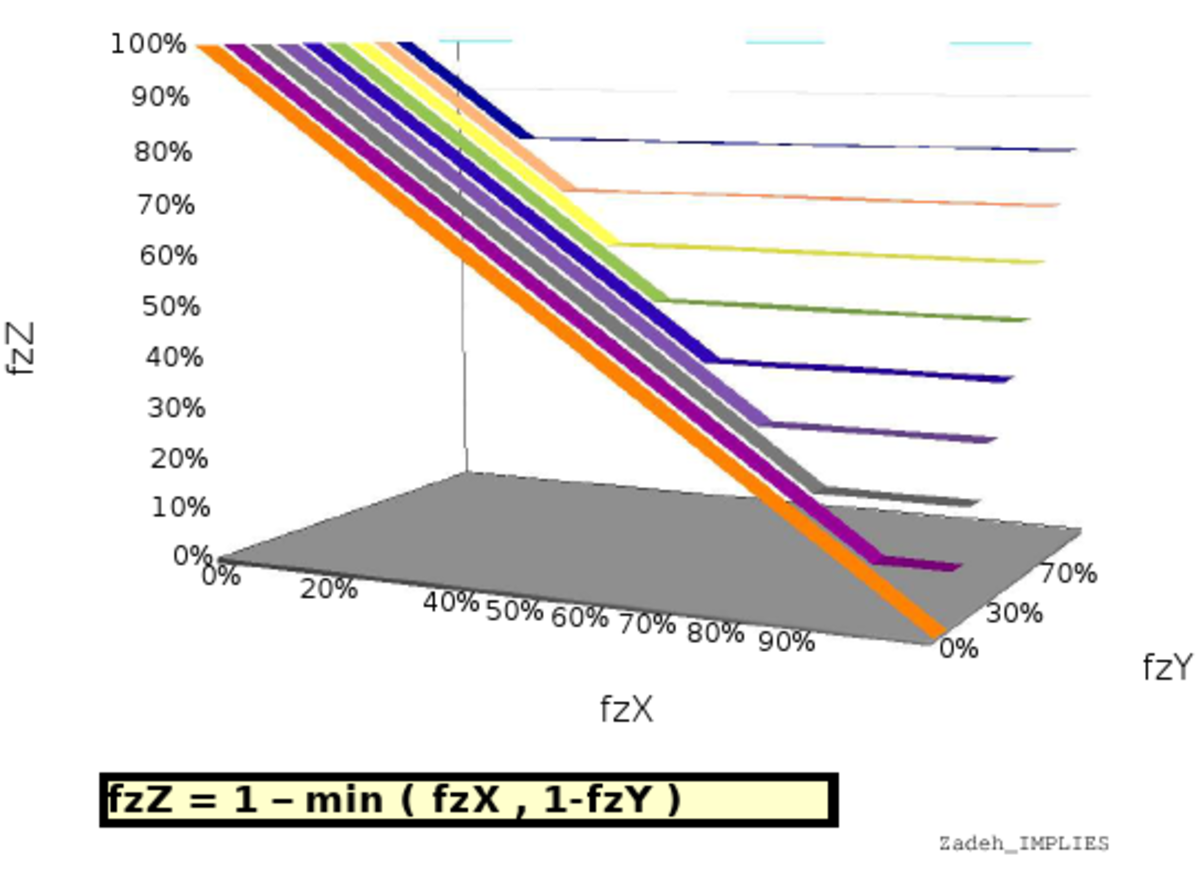
      fzImpliqueOk = Bool_IMPLIES( fzConnaitOrchidees, fzMembre )      fzImpliqueOk = Zadeh_IMPLIES( fzConnaitOrchidees, fzMembre )      fzImpliqueOk = HypPar_IMPLIES( fzConnaitOrchidees, fzMembre )      

Boolean IMPLIES

Zadeh IMPLIES

Hyperbolic Paraboloid IMPLIES

Implémentation

Les opérateurs ci-dessus s'implémenteront respectivement comme ceci :

      fzImpliqueOk = fzConnaitOrchidees ⇐ fzMembre       fzImpliqueOk = 1 - min( fzConnaitOrchidees, (1 - fzMembre) )      fzImpliqueOk = 1 - fzConnaitOrchidees + (fzConnaitOrchidees*fzMembre      

dans un cas extrême mais normal, avec fzConnaitOrchidees=0.8 et fzMembre=0.995, les valeurs trouvées seront respectivement

       1 (true)       0.995 (Zadeh)       0.996 (Hyperbolic Paraboloid)      

dans un cas considéré comme normal, avec fzConnaitOrchidees=0.8 et fzMembre=0.72, les valeurs trouvées seront respectivement

       0 (false) (la personne est moins membre qu'elle ne connait)       0.72 (Zadeh)       0.776 (Hyperbolic Paraboloid)      

dans un autre cas qui reste normal, la personne pouvant aussi être membre des amis des fleurs à cause de son amour des tulipes, avec fzConnaitOrchidees=0.66 et fzMembre=0.72, les valeurs trouvées seront respectivement

       1 (true)  (la personne est plus membre qu'elle ne connait)       0.72 (Zadeh)       0.772 (Hyperbolic Paraboloid)      

dans un cas assez douteux, avec fzConnaitOrchidees=0.5 et fzMembre=0.5, les valeurs trouvées seront respectivement

       1 (true)        0.5 (Zadeh)       0.75 (Hyperbolic Paraboloid)      

dans un cas anormal, avec fzConnaitOrchidees=0.8 et fzMembre=0.3, les valeurs trouvées seront respectivement

       0 (false)       0.3 (Zadeh)       0.44 (Hyperbolic Paraboloid)      

dans un cas anormal et extrême, avec fzConnaitOrchidees=0.8 et fzMembre=0.005, les valeurs trouvées seront respectivement

       0 (false)       0.2 (Zadeh)       0.204 (Hyperbolic Paraboloid)      

Utilisation pratique

Une application informatique qui viserait à proposer à un opérateur humain de traiter les cas anormaux en commençant par les plus suspects utiliserait les valeurs indiquées ci-dessus en gras et obtenues par la méthode identifiée Hyperbolic Paraboloid, particulièrement discriminante.

Il n'est pas sûr que cette application intéresse les amis des fleurs. Par contre, l'intérêt pour un service de médecine préventive (ou même pour un fleuriste) est compréhensible. Lorsque le nombre d'examens des cas suspects doit être plafonné (par exemple pour des raisons de temps, de coût, de dangerosité, etc), un pré-classement intelligent, fondé -sinon sur une théorie incontestée- du moins sur une technologie opérationnelle, peut s'avérer utile.

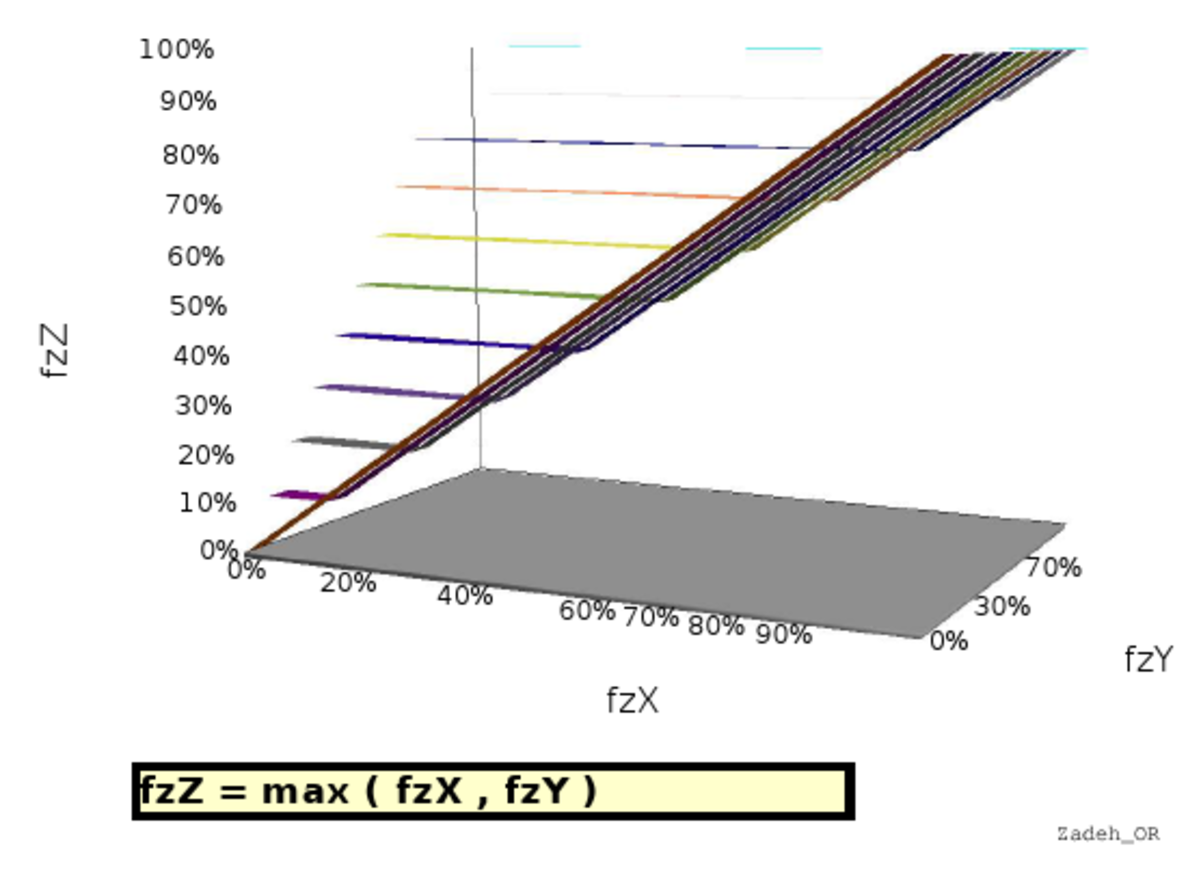
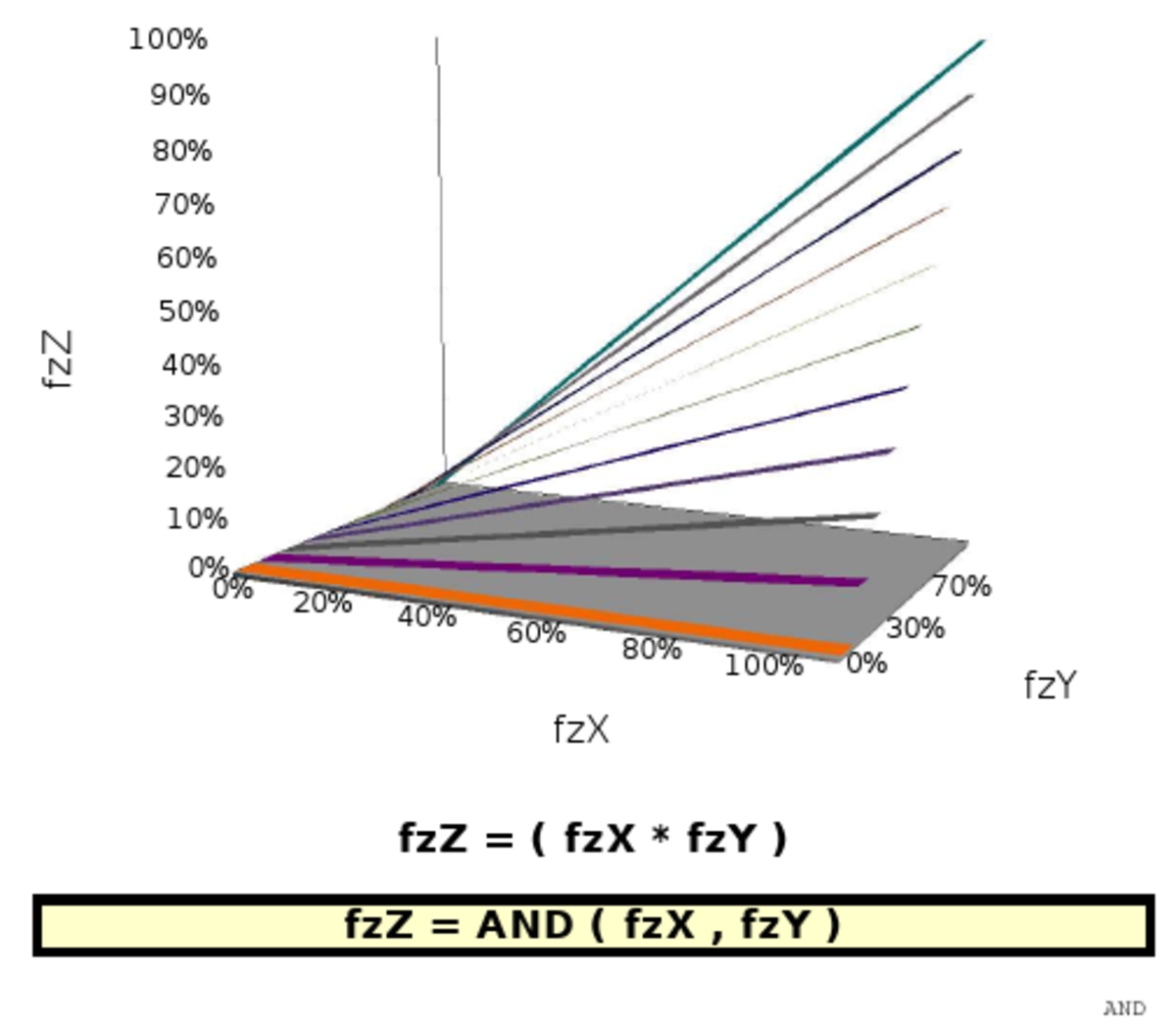
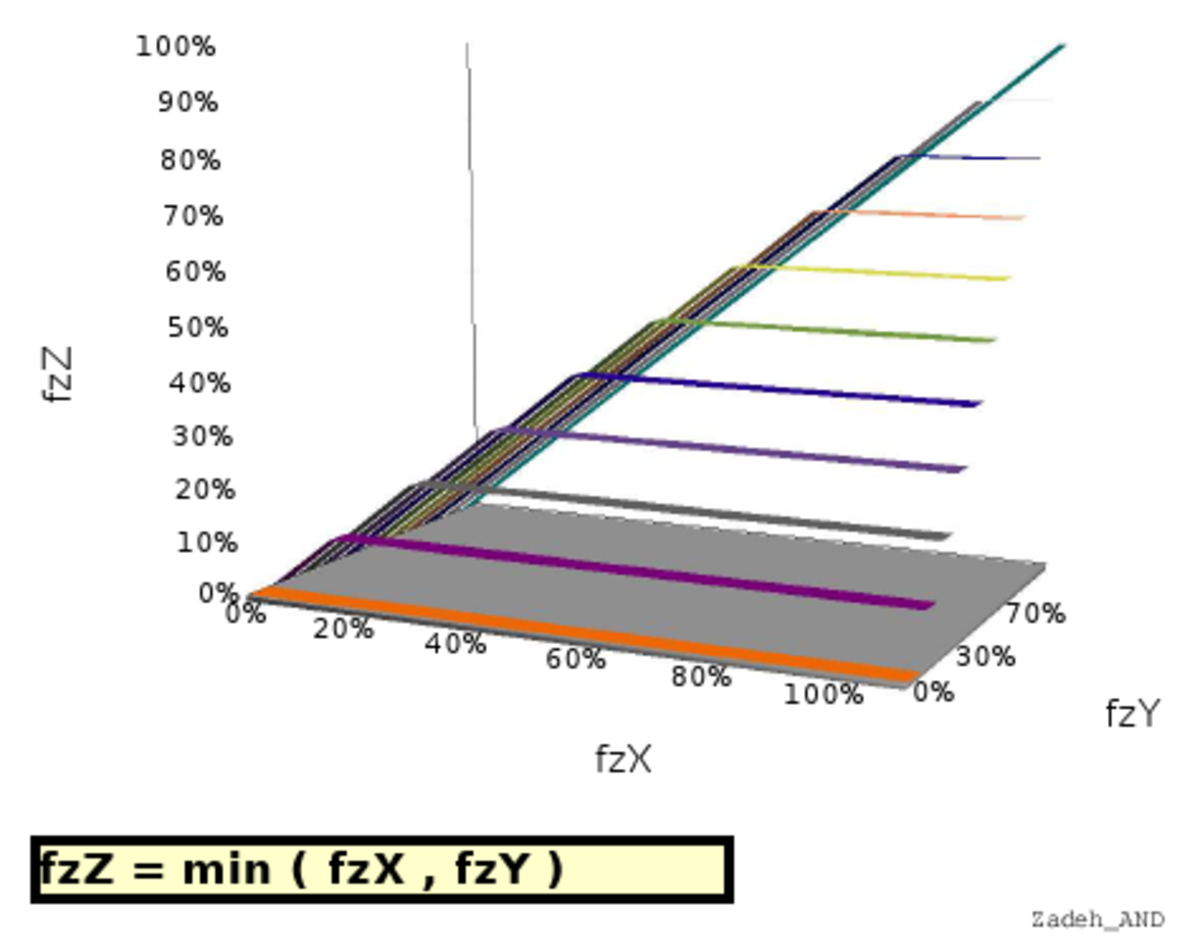
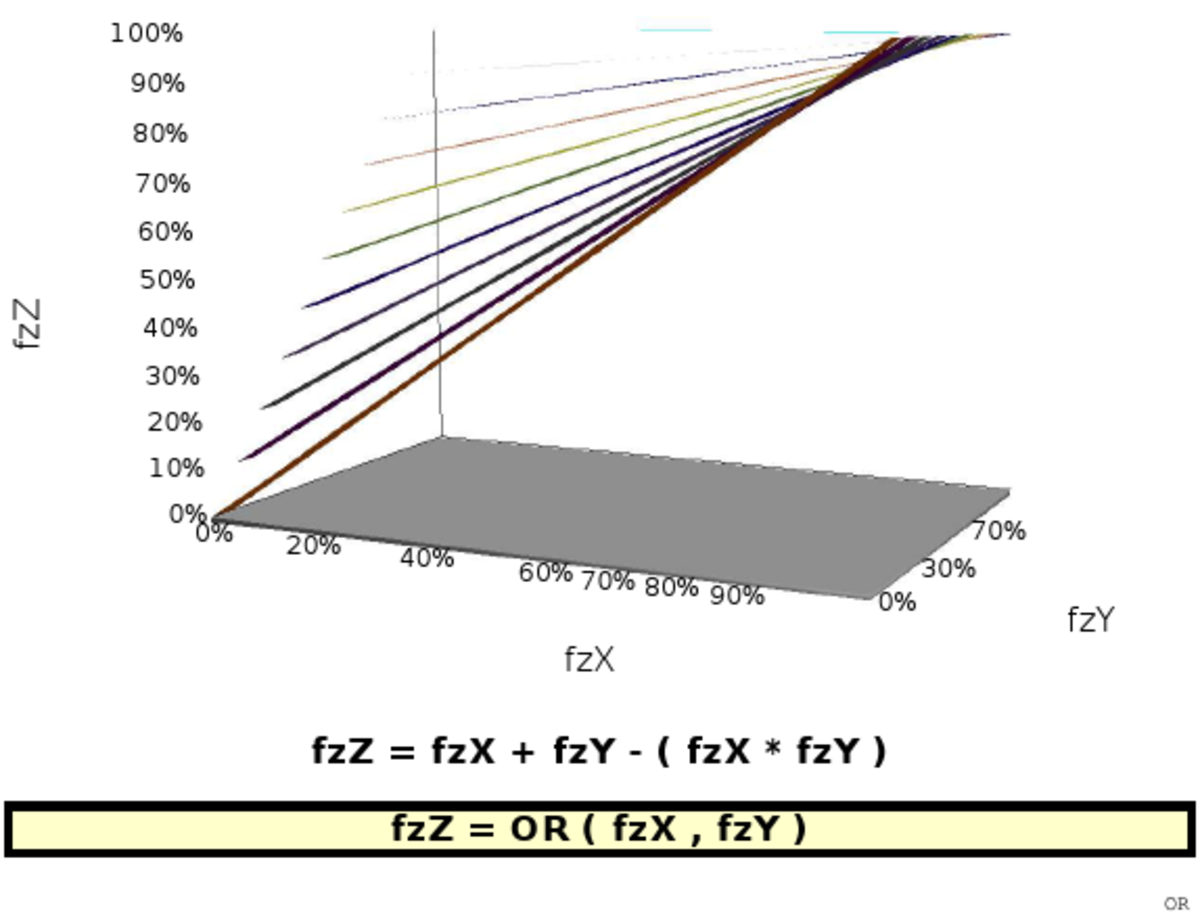
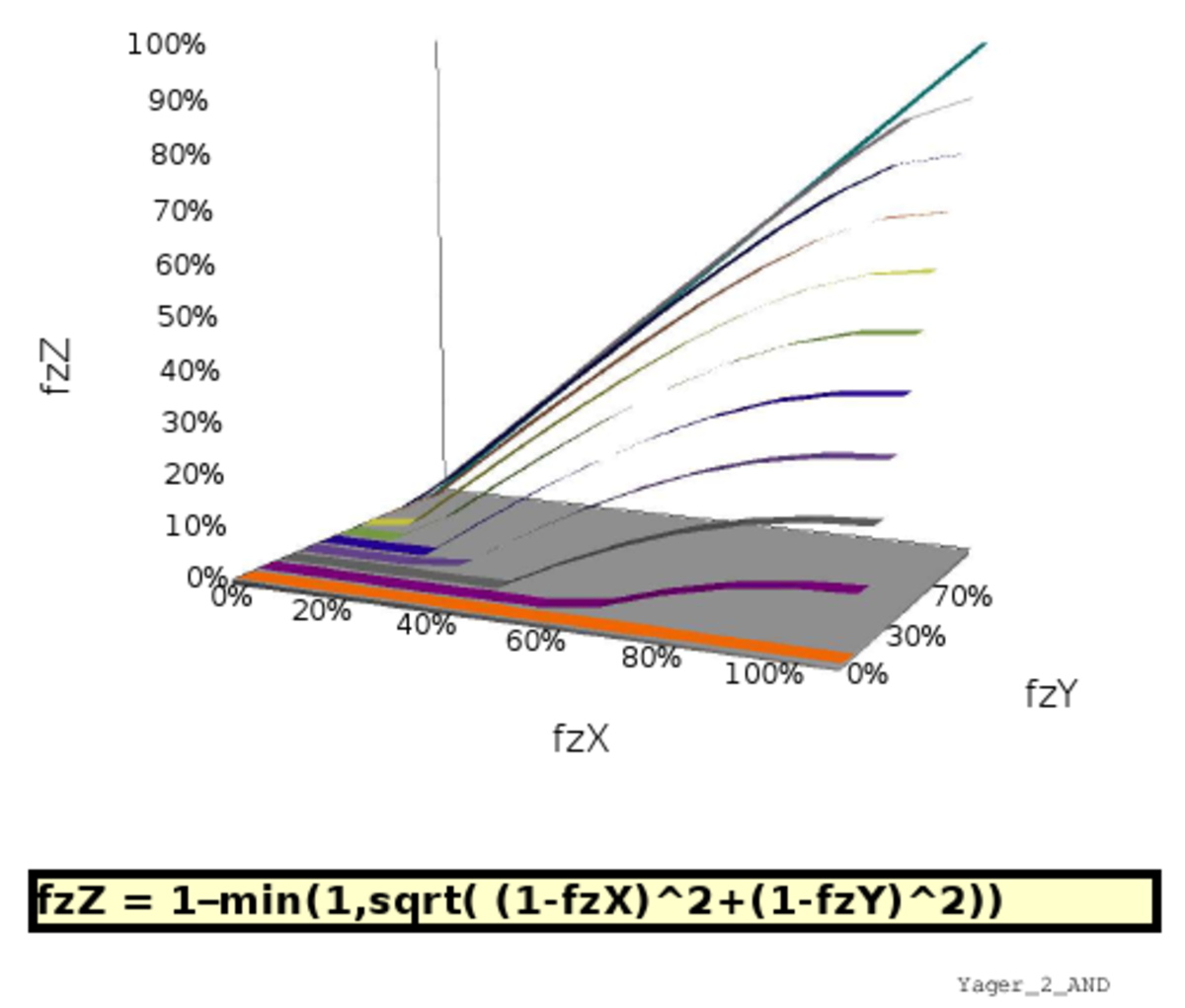
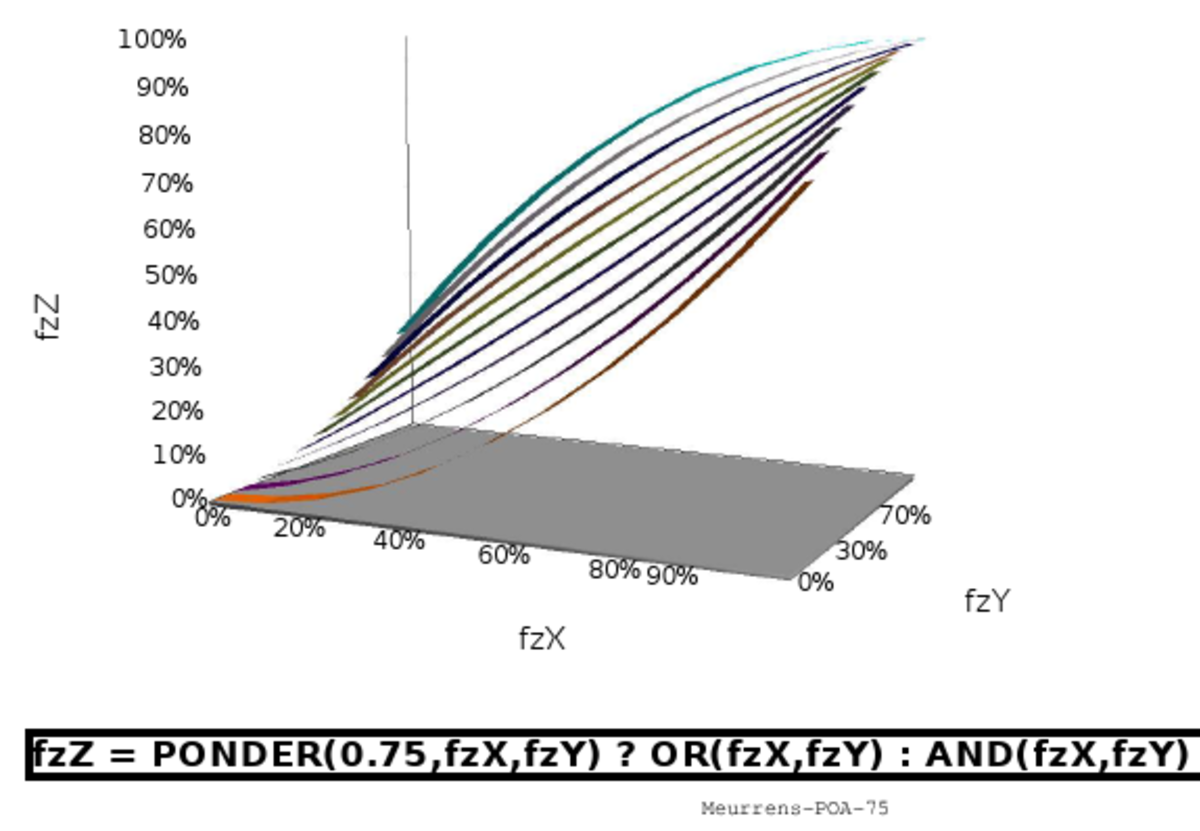
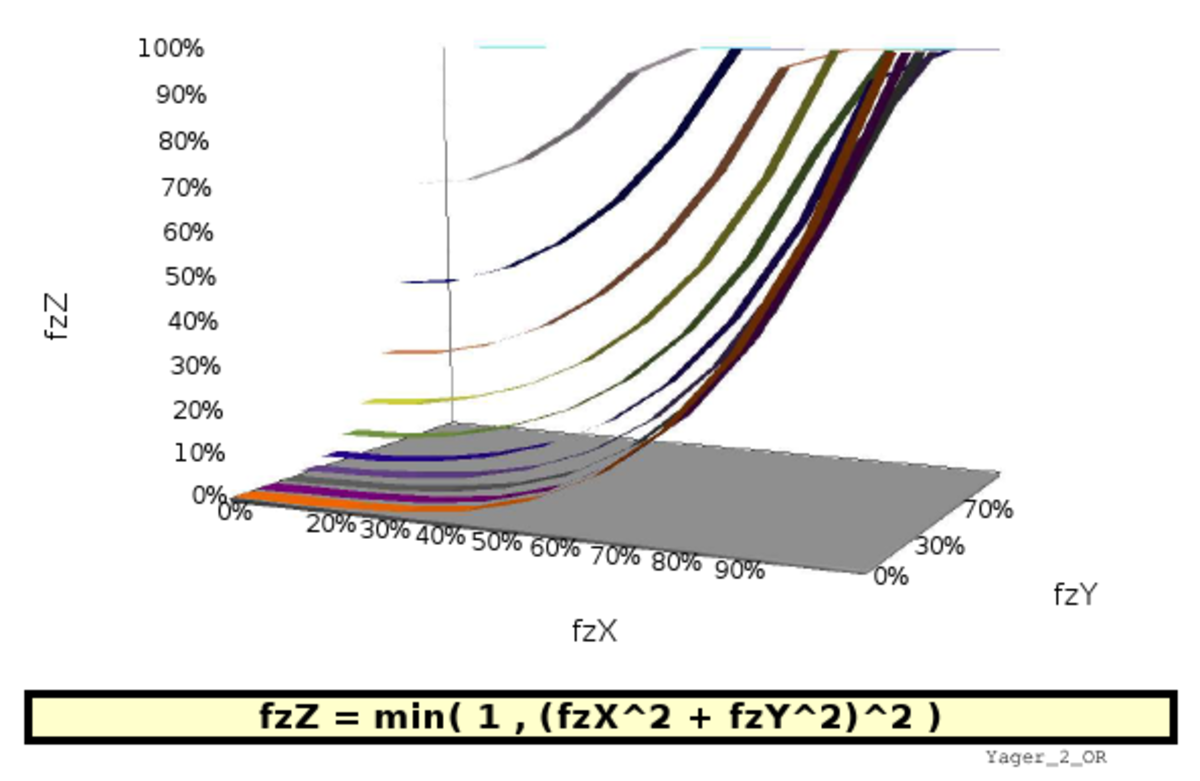
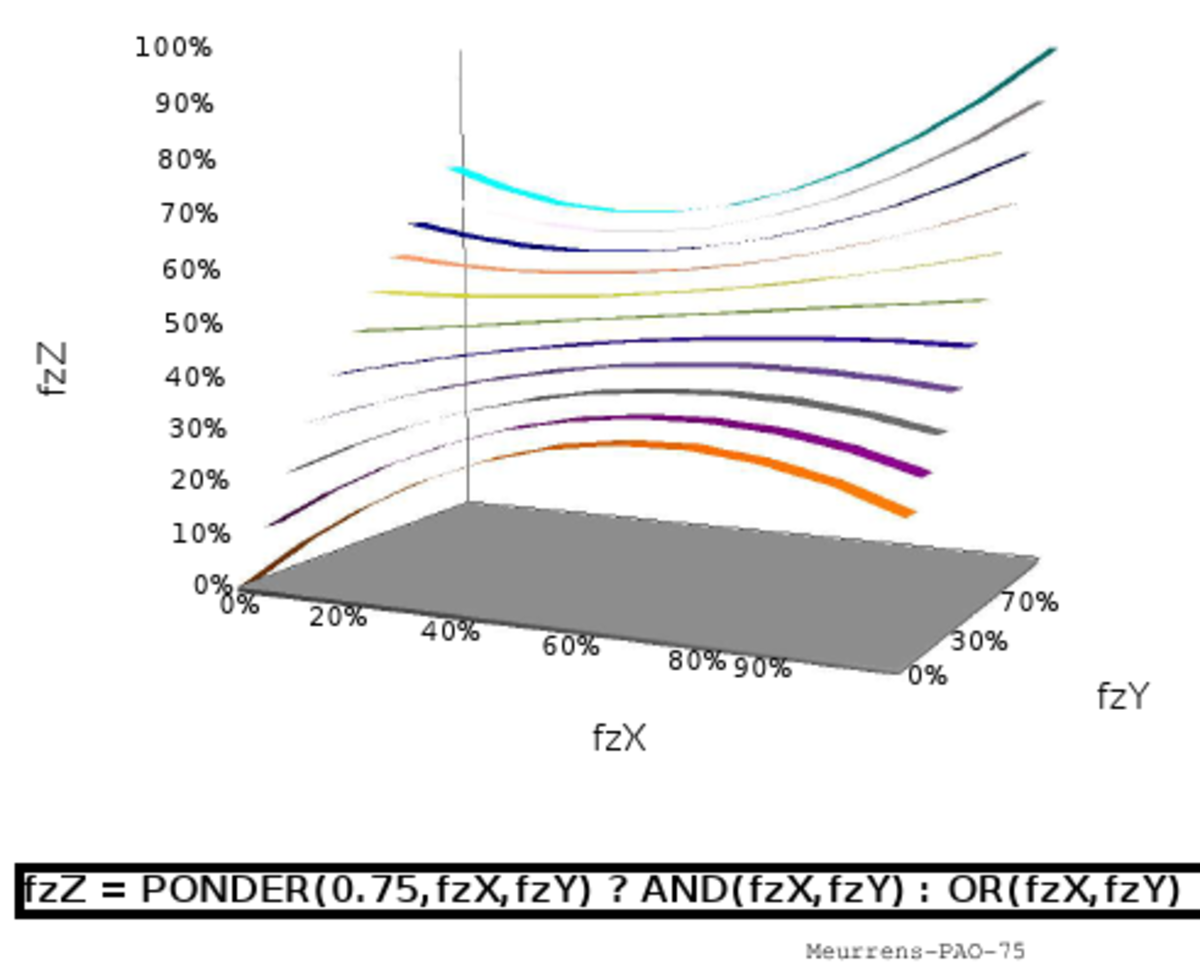
Représentation graphique

L'article commons:Fuzzy operator fournit de nombreuses représentations graphiques de quelques implémentations possibles des opérateurs fuzzy. On trouvera ci-dessous, à titre d'exemple, la représentation de huit implémentations différentes d'une opération qui viserait à apprécier la simultanéité de deux faits (jugés de poids équivalents dans les six images à gauche mais de poids différents dans les deux images de droite).

zadeh-AND

multiply-AND

yager-AND

mm-WEIGHT-OR-AND

zadeh-OR

add-OR

yager-OR

mm-WEIGHT-AND-OR