Logique floue - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Principe - Opérateurs flous - Combinaison de plusieurs entrées - Insuffisances en tant que théorie ? - Commande floue - La logique floue n'est pas la seule à parler d'incertitude

Combinaison de plusieurs entrées

Dans le cas d'une combinaison de plusieurs entrées (« Si le ciel est bleu et si j'ai le temps »), deux cas se présentent :

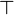
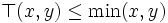
Les entrées sont liées par une fonction logique « ET » : dans ce cas, on peut considérer comme première approche seulement l'entrée ayant le degré de vérification le plus faible. En fait, il suffit de choisir un opérateur $\top$ tel que $\top(x,y)\leq \min(x,y)$ où $\top$ est appelée une t-norme. $min$ est la plus optimiste des t-normes.
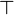
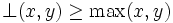
Les entrées sont liées par une fonction logique « OU » : dans ce cas, on peut considérer comme première approche seulement l'entrée ayant le degré de vérification le plus élevé. En fait, il suffit de choisir un opérateur $\bot$ tel que $\bot(x,y)\geq \max(x,y)$ où $\bot$ est appelée une t-conorme. $max$ est la plus pessimiste des t-conormes.

Il est techniquement possible de représenter toutes les opérations binaires de base en se basant sur la logique floue. En effet, à partir des opérateurs ET, OU et NON (AND, OR, NOT), on peut représenter les 8 opérations de base :

OU (OR) : A OR B = max(A, B);
ET (AND) : A AND B = min(A, B);
NON (NOT) : NOT A = 1 - A;
OU EXCLUSIF (XOR) : A XOR B = (A OR B) AND NOT (A AND B) = A + B - 2 × min(A, B);
NON-OU (NOR) : A NOR B = 1 - max(A, B);
NON-ET (NAND) : A NAND B = 1 - min(A, B);
NON-XOR (NXR) : A NXR B = 1 + 2 × min(A, B) - (A + B);
SUIVEUR (NOP) : NOP A = A.

Par ailleurs, la dimension décimale des variables de la logique floue permet d'effectuer des combinaisons non binaires :

Le produit : A.B ou A × B (équivalent en binaire à l'opération AND)
L'addition : A + B - A × B (équivalent en binaire à l'opération OR ; en effet, la simple addition dépasserait les bornes de l'interval [0 ; 1] dans certain cas)

Insuffisances en tant que théorie ?

Il existe une opinion qui dit que^[évasif] "La théorie des ensembles flous présente la particularité de n'avoir aucun théorème à proposer. C'est-à-dire que si elle peut rendre quelques services techniques, elle ne peut pour autant prétendre à un quelconque statut de science, et encore moins de théorie.". ^{[citation nécessaire]}

En fait, la logique floue a été formalisée^{[réf. souhaitée]} et un théorème (élémentaire, cependant) montre que dans le cas particulier où les propositions traitées ne sont pas floues, la logique floue se réduit à la logique classique.

D'autre part, bien que des détracteurs de la logique floue prétendent que^[évasif] "Le théorème de Cox-Jaynes montre d'une part que l'on peut représenter un état de connaissance incertaine par une probabilité, et d'autre part que tout moyen utilisé pour prendre des décisions sera soit isomorphe à la théorie des probabilités, soit incohérent"^{[citation nécessaire]}, ce théorème ne s'applique pas aux connaissances floues, qui ne sont généralement pas des connaissances incertaines (ce qui rend difficile, voire infondée, leur représentation par des probabilités).

Le flou est lié à la forme de la connaissance : son imprécision n'est donc pas de nature probabiliste. Par exemple, dire "l'âge de cette personne est autour de 30 ans" ne présume en rien de la probabilité de l'âge effectif de la personne. On peut mieux voir la distinction entre imprécision et probabilité en pondérant cette assertion : "je suis sûr que l'âge de cette personne est autour de 30 ans" où l'on peut retrouver ici à la fois une imprécision (sur la valeur de l'âge) et une certitude (sur le fait que cet âge soit autour de 30 ans). Ou aussi : "l'âge de cette personne est autour de 30 ans, avec une probabilité de 0.2" où l'on retrouve encore une connaissance floue ("autour de 30 ans") qui est relativisée par une probabilité de véracité.

La logique floue s'attache donc à une certaine forme des connaissances (leur imprécision) et propose un certain formalisme rigoureux permettant d'inférer de nouvelles connaissances. En cela, elle est complémentaire de la théorie des probabilités.

Pour illustrer encore ce propos, on peut citer l'exemple classique de Jim Bezdek qui permet de mieux différencier probabilité et imprécision : "On se trouve dans un désert, après des jours d'errance… Presque mort de soif, on trouve alors 2 bouteilles remplies d'un liquide. Sur la bouteille A, une étiquette annonce "potable avec un degré 0.9", et sur la bouteille B, l'étiquette dit "potable avec une probabilité 0.9". Laquelle de ces 2 bouteilles doit-on choisir ?". Si l'on traduit les indications des étiquettes, on en retire qu'en buvant la bouteille A, on pourra s'en tirer avec comme seuls risques, quelques problèmes intestinaux non mortels… Par contre, en buvant la bouteille B, il y a une probabilité non négligeable (10% de chance) que le liquide puisse être très nocif (acide…) et absolument pas buvable.

La théorie des possibilités a été introduite (aussi par Lotfi Zadeh en 1978) afin de permettre la prise en compte combinée à la fois de l'imprécision et de l'incertitude dans des connaissances.