Loi de Bernoulli - Définition
La liste des auteurs de cet article est disponible ici.
Distributions liées
Loi binomiale
Si
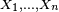
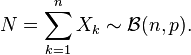
Loi de Poisson
Soit
![S_n=\sum_{k=1}^{a_n}\,X_{k,n}\quad\text{et}\quad\lambda_n\ =\ \mathbb{E}[S_n]=\sum_{k=1}^{a_n}\,p_{k,n}.\](https://static.techno-science.net/illustrationWebp/Definitions/autres/6/6541a45bb94abcc6be00442dca3ac601_a96e916a4013b7feeebfcec584b249a5.png)
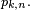
Inégalité de Le Cam — Pour tout ensemble A d'entiers naturels,
En particulier, si les deux conditions suivantes sont réunies :
alors Sn converge en loi vers la loi de Poisson de paramètre λ.
Les deux conditions ci-dessus entrainent que
Conséquence : paradigme de Poisson — La somme Sn d'un grand nombre de variables de Bernoulli indépendantes de petit paramètre suit approximativement la loi de Poisson de paramètre
![\scriptstyle\ \mathbb{E}[S_n]. \](https://static.techno-science.net/illustrationWebp/Definitions/autres/5/5727907d43850533ffb9dab459c30599_fcd46d89adba9157b1d4167ce679b4e5.png)
La loi de Poisson intervient souvent lorsqu'on compte des évènements rares comme les suicides d'enfants, les arrivées de bateaux dans un port ou les accidents dus aux coups de pied de cheval dans les armées (étude de Ladislaus Bortkiewicz). Le décompte des évènements rares se fait souvent au travers d'une , et la rareté des évènements se traduit par le fait que les paramètres de ces variables de Bernoulli sont petits (ainsi, la probabilité que chaque évènement survienne est faible).
- Ce paradigme reste pertinent, dans certaines conditions, si l'on relaxe l'hypothèse d' indépendance.
- Un exemple frappant est le nombre de points fixes d'une permutation tirée au hasard.
- Un autre exemple est le nombre de points isolés du graphe aléatoire, dont la convergence vers la loi de Poisson a permis à Erdös et Rényi de démontrer, en 1960, le théorème double-exponentiel.
- Le cas particulier an=n, pk,n=λ/n, λn=λ, de l'inégalité de Le Cam, précise la rapidité de convergence de la loi binomiale de paramètres n et λ/n vers la loi de Poisson de paramètre λ.
