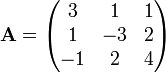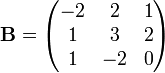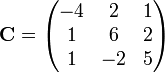Matrice à diagonale dominante - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En algèbre linéaire, une matrice carrée à coefficients réels ou complexes est dite à diagonale dominante lorsque le module de chaque terme diagonal est supérieur ou égal à la somme des modules des autres termes de sa ligne. Si
![A=((a_{i,j})_{i,j \in [\![1,n]\!] })](https://static.techno-science.net/illustration/Definitions/autres/8/892c212902f44b5d976583a916fba5b8_e10e40a59c910865c4616cfa60a7c936.png)
De la même manière, A est dite à diagonale strictement dominante lorsque
Exemples
La matrice
vérifie
-
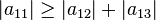
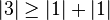
-
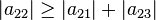
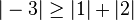
-
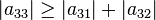
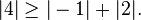
C'est donc une matrice à diagonale dominante.
La matrice
vérifie
-
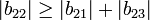
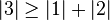
mais
-
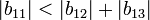
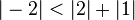
et
-
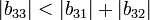
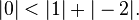
Ce n'est donc pas une matrice à diagonale dominante.
La matrice
vérifie
 car
car 
 car
car 
 car
car 
C'est donc une matrice à diagonale strictement dominante.
Lemme d'Hadamard
C'est un cas particulier du Théorème de Gerschgorin. Inversement, il peut servir de lemme pour démontrer ce dernier.
Enoncé
Si
![A=((a_{i,j})_{i,j\in [\![1,n]\!] })](https://static.techno-science.net/illustration/Definitions/autres/8/892c212902f44b5d976583a916fba5b8_e10e40a59c910865c4616cfa60a7c936.png)
Démonstration
Par la contraposée. Supposons A non inversible alors son noyau n'est pas réduit à zéro,
il existe donc :
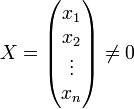
On a alors :
![\forall i \in [\![1,n]\!],\ \sum_{j=1}^n a_{i,j}x_j =0 .](https://static.techno-science.net/illustration/Definitions/autres/c/c8db679283738f74540dae3ea02e411b_585320486e64e83b2ad472d2490bbbbb.png)
Comme
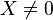
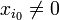
![|x_{i_0}|=\max \left\{{|x_i|, i \in [\![1,n]\!]}\right\}](https://static.techno-science.net/illustration/Definitions/autres/e/e07f23c1d0c398e0856f0b9e4b4d9bab_a963dddbecd54de4c92e296c1056651a.png)
On a :
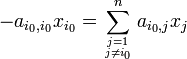
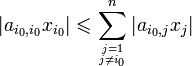
et comme :
![\forall j \in [\![1,n]\!],\ \frac{|x_j|}{|x_{i_0}|}\leqslant 1](https://static.techno-science.net/illustration/Definitions/autres/f/fceee9886690b56b4ae3d9d79503120d_9513ef89ba7fc3722b375c0b635dabed.png)
on obtient
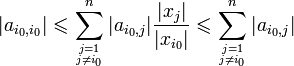
Finalement,
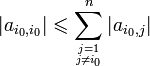
![\forall i \in [\![1,n]\!],\ |a_{i,i}|\ge\sum_{j=1 \atop j\neq i}^n |a_{i,j}|.](https://static.techno-science.net/illustration/Definitions/autres/a/a4d1db422d2be09caa0f34694e1a4ee6_6f592dbe074b77df82d152162a1db637.png)
![\forall i \in [\![1,n]\!],\ |a_{i,i}|>\sum_{j=1 \atop j\neq i}^n |a_{i,j}|.](https://upload.wikimedia.org/math/5/7/7/5778c1a3536c34e9a2e7881179961607.png)