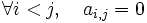Matrice triangulaire - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Introduction
En algèbre linéaire, les matrices triangulaires sont des matrices carrées dont une partie triangulaire des valeurs, délimitée par la diagonale principale, est nulle.
Matrices triangulaires supérieures
Ce sont des matrices carrées dont les valeurs sous la diagonale principale sont nulles :
A est triangulaire supérieure si et seulement si :
Propriétés des matrices triangulaires
- Une matrice triangulaire à la fois inférieure et supérieure est une matrice diagonale.
- Le produit de deux matrices triangulaires inférieures (respectivement supérieures) est une matrice triangulaire inférieure (respectivement supérieure).
- La transposée d'une matrice triangulaire supérieure est une triangulaire inférieure, et vice-versa.
- Une matrice triangulaire A est inversible si et seulement si tous ses termes diagonaux sont non nuls. Dans ce cas, son inverse est aussi une matrice triangulaire (supérieure si A était supérieure, inférieure sinon).
- Les valeurs propres d'une matrice triangulaire sont ses termes diagonaux.
- Le déterminant d'une matrice triangulaire est égal au produit de ses éléments diagonaux :
![\det\left((a_{i,j})_{(i,j)\in[\![1;n]\!]^2}\right) = \prod_{i=1}^n a_{i,i}](https://static.techno-science.net/illustrationWebp/Definitions/autres/c/c5478467f1eb272e8b04ee581713d5be_efab685bb36142d1e4ba96c18628f7c2.png)
Matrices triangulaires inférieures
Ce sont les matrices carrées dont les valeurs au-dessus de la diagonale principale sont nulles :
A est triangulaire inférieure si et seulement si :
