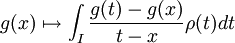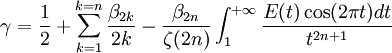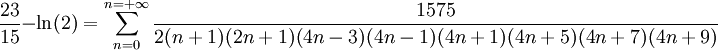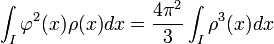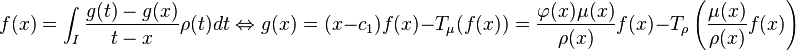Mesure secondaire - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Les plus belles applications
.
-
-
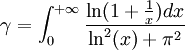
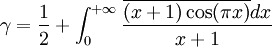
(la fonction
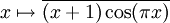
(avec E fonction partie entière et β2n nombre de Bernoulli d'ordre 2n).
-
-
-
-
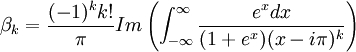
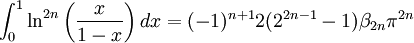
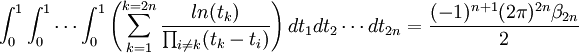
![\qquad \int_0^{+\infty}\frac{e^{-\alpha x}dx}{\Gamma(x+1)}=e^{e^{-\alpha}}-1+\int_0^{+\infty}\frac{1-e^{-x}}{\left[(\ln(x)+\alpha)^2+\pi^2\right]}\frac{dx}{x}](https://static.techno-science.net/illustration/Definitions/autres/4/44e12c1e4d16fa70029ffae5e38dcfe1_0e231cb10d39fdf0a8392479bda8e2ed.png)
![\qquad \int_0^{+\infty}\frac{e^{-\alpha x}dx}{\Gamma(x+1)}=e^{e^{-\alpha}}-1+\int_0^{+\infty}\frac{1-e^{-x}}{\left[(\ln(x)+\alpha)^2+\pi^2\right]}\frac{dx}{x}](https://static.techno-science.net/illustrationWebp/Definitions/autres/4/44e12c1e4d16fa70029ffae5e38dcfe1_0e231cb10d39fdf0a8392479bda8e2ed.png)
-
![\sum_{n=1}^{n=+\infty}\left(\frac{1}{n}\sum_{k=0}^{k=n-1}\frac{1}{\binom{n-1}{k}}\right)^2=\frac{4\pi^2}{9}=\int_0^{+\infty}4[\mathrm {Ei} (1,-x)+i\pi]^2e^{-3x}dx](https://static.techno-science.net/illustration/Definitions/autres/8/8690d736db80261f23b71aa36fcedbec_1733b8140ca1f5848cd7ccee6b94cbbf.png)
![\sum_{n=1}^{n=+\infty}\left(\frac{1}{n}\sum_{k=0}^{k=n-1}\frac{1}{\binom{n-1}{k}}\right)^2=\frac{4\pi^2}{9}=\int_0^{+\infty}4[\mathrm {Ei} (1,-x)+i\pi]^2e^{-3x}dx](https://static.techno-science.net/illustrationWebp/Definitions/autres/8/8690d736db80261f23b71aa36fcedbec_1733b8140ca1f5848cd7ccee6b94cbbf.png)
(Ei désigne ici la fonction exponentielle intégrale).
- Catalan =
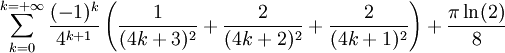
- Catalan =
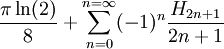
(La constante de Catalan est définie comme
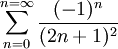
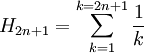
Si la mesure ρ est réductible de réductrice associée
Si la mesure ρ est réductible de mesure secondaire associée μ, alors si f est de carré intégrable pour μ, et si g est de carré intégrable pour ρ et orthogonale à P0 = 1 on a l'équivalence:
(c1 désigne le moment d'ordre 1 de ρ et Tρ l'opérateur
