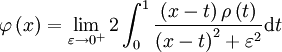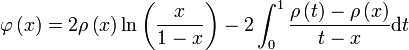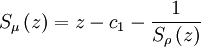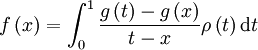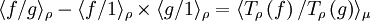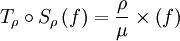Mesure secondaire - Définition

Introduction

En mathématiques, la mesure secondaire associée à une mesure de densité positive ρ est, lorsqu'elle existe, une mesure de densité positive μ qui rend orthogonaux les polynômes secondaires associés aux polynômes orthogonaux pour ρ.

Sous certaines hypothèses que nous préciserons plus loin, il est possible d'obtenir l'existence d'une telle mesure et même de l'exprimer :

Par exemple si on travaille dans l'espace de Hilbert

Avec dans le cas général :

Dans le cas où ρ est lipschitzienne :

Cette application est dite « réductrice » de ρ.

Dans un cadre plus général, μ et ρ sont reliées via leurs transformées de Stieltjes par la formule suivante :

où c₁ est le moment d'ordre 1 de la mesure ρ.

Ces mesures secondaires, et la théorie qui les entoure, conduisent à quelques résultats surprenants, et permettent de retrouver de façon élégante un bon nombre de formules classiques d'analyse, principalement autour des fonctions Γ d'Euler, ζ de Riemann, et du nombre γ d'Euler. Elles permettent aussi l'explicitation d'intégrales et de séries a priori difficiles avec une efficacité redoutable. Enfin elles permettent de résoudre des équations intégrales de la forme :

où g est la fonction inconnue, et conduisent à des théorèmes de convergence vers les mesures de Tchebychev et Dirac.

Les grandes lignes de la théorie

Soit un espace mesuré par une mesure de densité positive ρ sur un intervalle I et admettant des moments de tout ordre.

On peut construire une famille des polynômes orthogonaux pour la structure préhilbertienne induite par ρ.

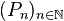
Appelons la famille des polynômes secondaires de la famille P. Sous certaines conditions il existe une mesure μ pour laquelle la famille Q est orthogonale. Cette mesure, que l'on peut expliciter en fonction de ρ est appelée mesure secondaire associée à la mesure initiale ρ.

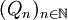
Lorsque ρ est une densité de probabilité, une condition suffisante pour que μ admettant des moments de tout ordre soit secondaire associée à ρ est que sa transformée de Stieltjes soit donnée par une égalité du type: , avec a constante arbitraire et désignant le moment d'ordre 1 de ρ.

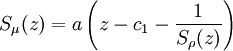
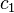
Pour a = 1 on obtient la mesure dite secondaire, remarquable au sens que pour la norme du polynôme P_n pour ρ coïncide exactement avec la norme du polynôme secondaire associé Q_n au sens de la mesure μ.

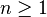
Dans ce cas primordial,et si l'espace engendré par les polynômes orthogonaux est dense dans , l'opérateur T_ρ défini par créant les polynômes secondaires peut se prolonger en une application linéaire reliant l'espace à et devient une isométrie si on la restreint à l'hyperplan H_ρ des fonctions orthogonales à P₀ = 1.

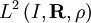
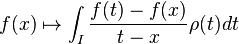
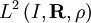
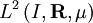
Pour des fonctions quelconques de carré intégrables pour ρ on obtient la formule plus générale de covariance :

La théorie se poursuit en introduisant la notion de mesure réductible, au sens que le quotient est élément de . On établit alors les résultats suivants :

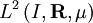
La réductrice de ρ est un antécédent de pour l'opérateur T_ρ. (En fait le seul antécédent élément de H_ρ).

Pour toute fonction de carré intégrable pour ρ, on a la formule dite de réduction : .

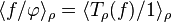
L'opérateur défini sur les polynômes, se prolonge en une isométrie S_ρ reliant l'adhérence de l'espace de ces polynômes dans à l'hyperplan H_ρ muni de la norme induite par ρ.

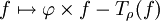
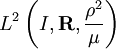
Sous certaines conditions restrictives l'opérateur S_ρ agît comme adjoint de T_ρ pour le produit scalaire induit par ρ.

Enfin les deux opérateurs sont reliés aussi, sous réserve que les images en question soient définies, par la formule fondamentale de composition :