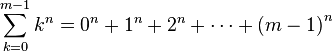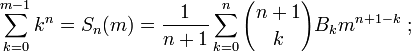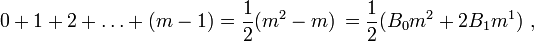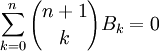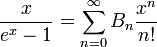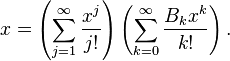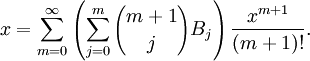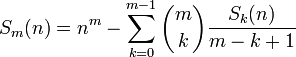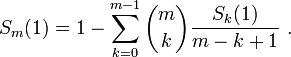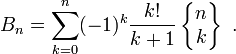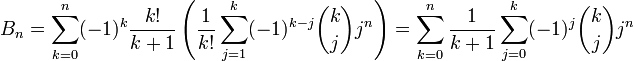Nombre de Bernoulli - Définition

Introduction

En mathématiques, les nombres de Bernoulli, notés (ou parfois , pour ne pas les confondre avec les polynômes de Bernoulli), constituent une suite de nombres rationnels, qui ont d'abord été étudiés par Jacques Bernoulli (ce qui a conduit Abraham de Moivre à leur donner le nom que nous connaissons aujourd'hui) en cherchant des formules pour exprimer les sommes du type :

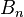
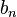
pour différentes valeurs de l'entier n, mais qui apparaissent dans de très nombreuses applications, depuis la formule d'Euler-Maclaurin jusqu'à l'approche par Kummer du dernier théorème de Fermat.

Introduction : sommes de puissances

L'expression est toujours un polynôme en m, de degré , dont les coefficients définissent les nombres de Bernoulli B_n de la façon suivante :

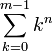
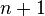
ces polynômes sont également liés aux polynômes de Bernoulli  : on a (pour tout n et m) S_n(m) = (B_{n + 1}(m) − B_{n + 1}(0)) / (n + 1). Par exemple, en donnant à n la valeur 1, on obtient :

ce qui montre que B₀ = 1 et B₁ = − 1 / 2 (on utilise parfois la notation pour distinguer les nombres de Bernoulli des nombres de Bell).

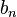
On verra plus bas qu'il est également possible de les calculer par récurrence, obtenant :

(avec la condition initiale : ).

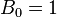
Les nombres de Bernoulli peuvent aussi être définis par l'intermédiaire de fonctions génératrices. Leur fonction génératrice exponentielle est , de telle sorte que :

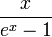
pour tout x de valeur absolue inférieure à (le rayon de convergence de cette série entière).

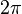
Cette définition peut être montrée équivalent à la précédente à l'aide d'un raisonnement par récurrence : le premier terme de la série est clairement B₀ (par prolongement par continuité). Pour obtenir la récurrence, on multiplie les deux côtés de l'équation par e^x − 1. Alors, en utilisant les séries de Taylor pour la fonction exponentielle,

En développant ceci en produit de Cauchy et en réarrangeant légèrement, on obtient

Il est clair, à partir de cette dernière égalité, que les coefficients dans cette série de puissances satisfont la même récurrence que celle des nombres de Bernoulli.

Formules de récurrence et formules explicites

Pour définir les nombres de Bernoulli par récurrence, repartons des sommes . On remarque que , et donc, d'après la formule du binôme, que  ; le terme en S_{m + 1} s'élimine, et on obtient finalement (après réindexation)

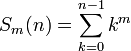
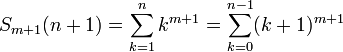
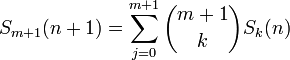
pour tous les entiers n ≥ 0, m ≥ 0, 0⁰ étant pris égal à 1, ce qu'on peut voir comme une définition par récurrence des S_m(n), avec pour base S₀(n) = 1 pour tout n ; c'est cette approche qui permet de démontrer que les coefficients de S_m(n) sont bien de la forme donnée dans l'introduction. Prenant ainsi n = 1, on obtient

Or on a vu que pour on a (par définition)  ; on obtient ainsi la récurrence exposée en introduction :

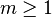
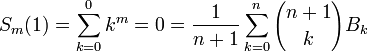
On peut en fait également définir les B_n sans récurrence : utilisant les nombres de Stirling (de deuxième espèce), on a (pour n>1)

d'où (en utilisant les formules explicites pour les nombres de Stirling, et en simplifiant)

On trouve souvent dans la littérature l'affirmation selon laquelle des formules explicites pour les nombres de Bernoulli n'existent pas ; les deux dernières équations montrent qu'il n'en est rien. En fait, dès 1893, Louis Saalschütz (de) recensait un total de 38 formules explicites, donnant généralement des références bien plus anciennes.