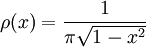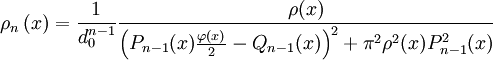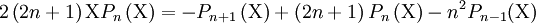Mesure secondaire - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Les grandes lignes de la théorie - Suite (ρn) des mesures secondaires - Cas de la mesure secondaire de la mesure de Lebesgue, et quelques autres exemples - Les plus belles applications

Suite (ρn) des mesures secondaires

La mesure secondaire $μ$ associée à une densité de probabilité $ρ$ a son moment d'ordre 0 égal à $d 0 = c 2 - (c 1) 2$ , ( $c 1$ et $c 2$ désignant les moments respectifs d'ordre 1 et 2 de $ρ$ ).

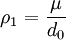
Pour pouvoir itérer le procédé on normalise alors $μ$ en définissant $\rho_1 =\frac{\mu}{d_0}$ qui devient à son tour une densité de probabilité appelée naturellement mesure secondaire normalisée associée à $ρ$ .

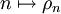
On peut alors définir de proche en proche à partir de $ρ 0 = ρ$ la suite $n\mapsto \rho_n$ ,chaque terme étant la mesure secondaire normalisée du précédent.

Il est possible d'expliciter la densité $ρ n$ en utilisant les polynômes orthogonaux $P n$ pour $ρ$ , les polynômes secondaires $Q n$ et la réductrice associée $\varphi$ . Cela donne la formule :

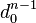
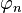
Le coefficient $d_0^{n-1}$ s'obtient facilement à partir des coefficients dominants des polynômes $P n - 1$ et $P n$ . On peut également expliciter la réductrice $\varphi_n$ associée à $ρ n$ , ainsi que les polynômes orthogonaux correspondant à $ρ n$ .

Un très beau résultat concerne l'évolution de ces densités lorsque l'indice tend vers l'infini et que le support des mesures est l'intervalle standard $\left[0,1\right]$ .

Soit la relation de récurrence à trois termes : $x P n (x) = t n P n + 1 (x) + s n P n (x) + t n - 1 P n - 1 (x)$ .

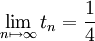
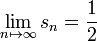
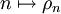
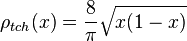
Si $\lim_{n \mapsto \infty}t_n=\frac{1}{4}$ et $\lim_{n \mapsto \infty}s_n=\frac{1}{2}$ , alors la suite $n\mapsto \rho_n$ converge complètement vers la densité de Tchebychev de deuxième forme $\rho_{tch}(x)=\frac{8}{\pi}\sqrt{x(1-x)}$ .

Ces conditions limites sont vérifiées par une très large classe de densités classiques.

Mesures équinormales

On appelle ainsi deux mesures conduisant à la même densité secondaire normalisée. Il est remarquable que les éléments d'une classe donnée de même moment d'ordre 1 soient reliés par une homotopie. Plus précisément, si la densité $ρ$ a son moment d'ordre 1 égal à $c 1$ , ces densités équinormales à $ρ$ seront donnés par une formule du type: $\rho_{t}(x)=\frac{t\rho(x)}{\left[\left(t-1\right)(x-c_1)\frac{\varphi\left(x\right)}{2}-t\right]^2+\pi^2\rho^2(x)(t-1)^2(x-c_1)^2}$ , t décrivant un intervalle contenant ]0, 1].

Si $μ$ est la mesure secondaire de $ρ$ , celle de $ρ t$ est $t μ$ .

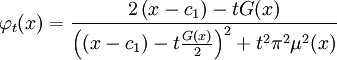
La réductrice de $ρ t$ est : $\varphi_t(x)=\frac{2\left(x-c_1\right)-tG(x)}{\left((x-c_1)-t\frac{G(x)}{2}\right)^2+t^2\pi^2\mu^2(x)}$ en notant $G (x)$ la réductrice de $μ$ .

Les polynômes orthonormaux pour la mesure $ρ t$ sont explicités à partir de $n = 1$ par la formule:

$P_n^t(x)=\frac{1}{\sqrt{t}}\left[tP_n(x)+(1-t)(x-c_1)Q_n(x)\right]$ avec $Q n$ secondaire associé à $P n$

Il est remarquable aussi que, au sens des distributions, la limite lorsque $t$ tend vers 0 par valeur supérieure de $ρ t$ soit la mesure de Dirac concentrée en $c 1$ .

Pour exemple, les densités équinormales à la mesure de Tchebychev de deuxième forme sont définies par : $\rho_t(x)=\frac{2t\sqrt{1-x^2}}{\pi\left[t^2+4(1-t)x^2\right]}$ , avec $t$ décrivant ]0,2]. La valeur $t$ =2 donne la mesure de Tchebychev de première forme.

Cas de la mesure secondaire de la mesure de Lebesgue, et quelques autres exemples

Mesure secondaire de Lebesgue

La mesure de Lebesgue sur l'intervalle standard $\left[0,1\right]$ est obtenue en prenant la densité constante $ρ(x) = 1$ .

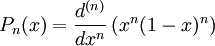
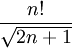
Les polynômes orthogonaux associés sont appelés polynômes de Legendre et peuvent être explicités par $P_n(x)=\frac{d^{(n)}}{dx^n}\left(x^n(1-x)^n\right)$ . La norme de $P n$ vaut $\frac{n!}{\sqrt{2n+1}}$ . La relation de récurrence à trois termes s'écrit :

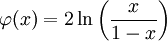
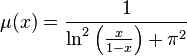
La réductrice de cette mesure de Lebesgue est donnée par $\varphi(x)=2\ln\left(\frac{x}{1-x}\right)$ . la mesure secondaire associée s'explicite alors comme : $\mu(x)=\frac{1}{\ln^2\left(\frac{x}{1-x}\right)+\pi^2}$ .

Exemples de mesures réductibles

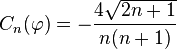
Si on normalise les polynômes de Legendre, les coefficients de Fourier de la réductrice $\varphi$ par rapport à ce système orthonormé sont nuls pour un indice pair et données par $C_n(\varphi)=-\frac{4\sqrt{2n+1}}{n(n+1)}$ pour un indice $n$ impair.

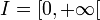
Les polynômes de Laguerre sont liés à la densité $ρ(x) = e - x$ sur l'intervalle $I=\left[0,+\infty \right[$ .

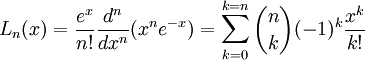
Ils sont explicités par $L_n(x)=\frac{e^x}{n!}\frac{d^n}{dx^n}(x^ne^{-x})=\sum_{k=0}^{k=n}\binom{n}{k}(-1)^k\frac{x^k}{k!}$ et sont normés.

la réductrice associée est définie par $\varphi(x)=2\left[\ln(x)-\int_0^{+\infty}e^{-t}\ln|x-t|dt\right]$ .

Les coefficients de Fourier de la réductrice $\varphi$ par rapport aux polynômes de Laguerre sont donnés par :

. Ce coefficient

n'est autre que l'opposé de la somme des éléments de la ligne d'indice

n

du tableau des nombres triangulaires harmoniques de Leibniz.

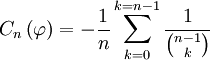
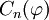
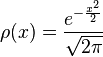
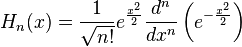
Les polynômes d'Hermite sont associées à la densité de Gauss $\rho(x)=\frac{e^{-\frac{x^2}{2}}}{\sqrt{2\pi}}$ sur $I=\ R$ . Ils sont explicités par $H_n(x)=\frac{1}{\sqrt{n!}}e^{\frac{x^2}{2}}\frac{d^n}{dx^n}\left(e^{-\frac{x^2}{2}}\right)$ et sont normés. La réductrice associée est définie par :

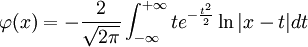
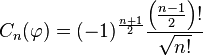
Les coefficients de Fourier de la réductrice $\varphi$ par rapport au système des polynômes d'Hermite sont nuls pour un indice pair et données par $C_n(\varphi)=(-1)^{\frac{n+1}{2}}\frac{\left(\frac{n-1}{2}\right)!}{\sqrt{n!}}$ pour un indice $n$ impair.

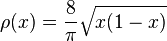
La mesure de Tchebychev de deuxième forme est définie par la densité $\rho(x)=\frac{8}{\pi}\sqrt{x(1-x)}$ sur l'intervalle [0,1]. C'est la seule qui coïncide avec sa mesure secondaire normalisée sur cet intervalle standard. Sous certaines conditions elle apparait comme limite de la suite des mesures secondaires normalisées d'une densité donnée.

Exemples de mesures non réductibles.

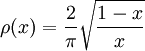
Mesure de Jacobi de densité $\rho(x)=\frac{2}{\pi}\sqrt{\frac{1-x}{x}}$ sur ]0,1[.

Mesure de Tchebychev de première forme de densité $\rho(x)=\frac{1}{\pi\sqrt{1-x^2}}$ sur ]-1,1[.

Les grandes lignes de la théorie

Les plus belles applications

Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜

Le rôle méconnu de la décharge dans l'usure des batteries 🔋

La fonte des glaces déplace les pôles: quelles conséquences ? 🌍

L'appareil photo de votre smartphone peut détecter l'antimatière 📱

Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐

Un mosasaure géant découvert dans le Mississippi 🦕

Problème, les galaxies meurent plus tôt que prévu 🌀

Ce lien entre cannabis et troubles psychotiques 🧠

Une révolution dans le refroidissement des puces électroniques ? 🔥

Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀

Lucy survole un astéroïde en forme de cacahuète 🚀

Découverte du fossile d'un dinosaure géant méconnu 🦕

Mars avait-elle un champ magnétique unilatéral ? 🔍

Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇

Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁

L'électroluminescence du graphène, une découverte inattendue ! 💡

Cet objet métallique n'a pas été fabriqué sur Terre 🔧

Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡

Cette super-Terre brûle les attentes des astronomes 🔥

Découverte exceptionnelle de fossiles d'amphibiens géants 🐸

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️

Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜

Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️

Cette vitamine développe les fonctions cognitives du cerveau 🧠

Comment des impacts géants vaporisent les corps planétaires ☄️

Les Américains riches vivent moins longtemps que les Européens pauvres 💰

Page générée en 0.110 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise