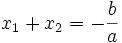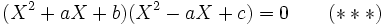Méthode de Descartes - Définition

Introduction

La méthode de Descartes dite par coefficients indéterminés permet de résoudre les équations du second, mais surtout du quatrième degré.

René Descartes utilise pour ceci la factorisation des polynômes de degré N sous la forme avec les n racines réelles ou complexes (voir Théorème de d'Alembert-Gauss) qu'il est alors l'un des premiers mathématiciens à maîtriser.

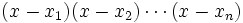
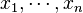
Pour résoudre le second degré, on part alors de la relation parfois dite de François Viète que l'on obtient en développant :

On pose alors

avec p une quantité réelle que l'on va chercher à déterminer dans l'autre relation.

Cette astuce est très importante : lorsqu'on a une somme de deux nombres A et B valant un réel C, on peut toujours écrire A comme la somme de la moitié de C et d'une certaine quantité; B, pour maintenir l'égalité A + B = C, vaudra forcément la moitié de C moins cette quantité.

On arrive alors à

ce qui amène par simple développement à p, puis aux deux racines, dont la formule est célèbre!

Cette méthode sert plus particulièrement à résoudre les équations du quatrième degré; il faut d'abord voir le polynôme

( auquel on s'est ramené par division par le coefficient de X puis une translation algébrique qui supprime le X à la puissance 3, voir les articles sur la Méthode de Ferrari et la Méthode de Cardan pour plus d'informations ) comme le produit de deux polynômes du second degré, et non pas comme le produit de quatre polynômes du premier degré ; les coefficients doivent être trouvés de sorte qu'en développant, on trouve bien les coefficients A, B, et C On pose donc

Ceci amène à un système traitable, le lecteur pourra vérifier en développant :

Le but étant ensuite de n'avoir plus qu'à résoudre deux équations du second degré pour sortir les quatre racines !

En soustrayant les deux premières lignes, on obtient

.

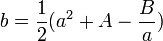
En additionnant les deux premières lignes, on obtient

.

Dans la dernière expression, on exprime b et c entièrement en fonction de a, ce qui aboutit à une équation dite résolvante, en développant un peu :

qui, en posant z = a², se ramène à un équation du troisième degré, la formule de Cardan donne donc à tous les coups un réel solution dont la racine carré vaudra a :

b et c se trouvent facilement avec les relations ci-dessus et au final, on trouvera des formules équivalentes à celles de Ferrari.

Exemple

Nous nous proposons de résoudre l'équation :

Posons :

En remplaçant dans l'équation, on obtient :

En développant l'équation :

Et en identifiant avec l'équation (**), on obtient:

En soustrayant les deux premières lignes, on obtient :

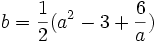
En additionnant les deux premières lignes, on obtient :

Portons maintenant ces valeurs de b et c dans (3), on obtient :

Qui se met sous la forme :

En multipliant par a² et en développant, on obtient :

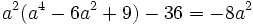
Et finalement :

Posons :

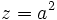
On obtient :

Cette équation admet pour racine évidente :

(S'il n'y a pas de racines évidentes, on peut résoudre l'équation en utilisant, par exemple, la méthode de Cardan)

On en déduit :

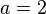
Et par suite :

En reportant les valeurs de a, b, c dans (***), on obtient :

On est donc ramené à résoudre les deux équations :

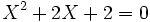
Les discriminants de ces deux équations sont :

Pour la première équation :

Pour la deuxième équation :

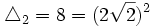
Nous en déduisons les quatre valeurs possibles de X.

Pour la première équation :

Pour la deuxième équation :

En reportant ces quatre valeurs de X dans (*), on obtient :

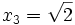
Qui sont bien les quatre racines de l'équation à résoudre.