Vendredi 13 Décembre 2024
Rechercher 🔍

Méthode de Cardan - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Formules de Cardan - Exemples - Principe de la méthode - Remarque historique

Introduction

La méthode de Cardan, proposée par Jérôme Cardan dans son ouvrage Ars Magna publié en 1545, est une méthode permettant de résoudre toutes les équations du troisième degré.

Cette méthode permet de mettre en place des formules, appelées formules de Cardan, donnant en fonction de p et q les solutions de l'équation :

z^3+pz + q= 0 ~

Elle permet de prouver que les équations de degré 3 sont résolubles par radicaux. Seules les équations de degré 1, 2, 3, 4 sont génériquement résolubles par radicaux, c’est-à-dire que seules ces équations possèdent des méthodes générales de résolutions donnant les solutions en fonction des coefficients du polynôme en utilisant seulement les quatre opérations habituelles sur les nombres rationnels, et l'extraction des racines nièmes.

Formules de Cardan

Considérons l'équation

z^3+pz + q= 0\,

On calcule le discriminant \Delta = q^2 + \frac{4}{27}p^3\, et on étudie son signe.

(Remarque : Il existe aussi la notion de "discriminant écriture réduite" en posant p = 3p' , q = 2q' et \Delta = 4 \Delta'\,  ; cela s'écrit \Delta' = q'^2 + p'^3\, )

Si l'on part de l'équation générale a x^3 + b x^2 + c x + d = 0\, , on se ramène à la forme réduite en posant \textstyle{x = z - \frac{b}{3a}} , p = - \frac{b^2}{3a^2} + \frac{c}{a} et q = \frac{b}{27a}\left(\frac{2b^2}{a^2}-\frac{9c}{a}\right)+\frac{d}{a} .

Dans ce qui suit, on suppose p et q réels - bien que la méthode soit valable aussi s'ils sont complexes.

Si Δ est positif

L'équation possède alors une solution réelle et deux complexes. On pose

u = \sqrt[3]{\frac{-q + \sqrt{\Delta}}{2}} \mbox{ et } v = \sqrt[3]{\frac{-q - \sqrt{\Delta}}{2}} \mbox{ soit encore } u = \sqrt[3]{-q'+\sqrt{\Delta'}} \mbox{ et } v = \sqrt[3]{-q'-\sqrt{\Delta'}}

La seule solution réelle est alors z_0 = u + v\, . Il existe également deux solutions complexes conjuguées l'une de l'autre \begin{cases}z_1= j u +\bar{j} v \\ z_2= j^2u +\overline{j^2}v \end{cases}   où   j = -\frac{1}{2} + i \frac{\sqrt{3}}{2} = e^{i \frac{2\pi}{3}} .

Si Δ est nul

L'équation possède alors deux solutions réelles, une simple et une double :

\begin{cases}z_0= 2\sqrt[3]{\frac{-q}{2}} = -2\sqrt{\frac{-p}{3}} = \frac{3q}{p} \\ z_1=z_2= -\sqrt[3]{\frac{-q}{2}} = \sqrt{\frac{-p}{3}} = \frac{-3q}{2p} \end{cases}

Si Δ est négatif

L'équation possède alors trois solutions réelles. Toutefois, il est nécessaire de faire une incursion dans les complexes pour toutes les trouver (voir ). Les solutions sont les sommes de deux complexes conjugués j^ku\, et \overline{j^ku} où u=\sqrt[3]{\frac{-q + i\sqrt{|\Delta|}}{2}} et k\in\{0,1,2\}\, , soit l'ensemble suivant :

\begin{cases}z_0 = u +\bar{u} \\ z_1 = j u +\overline{ju} \\ z_2= j^2u +\overline{j^2u} \end{cases}

La forme réelle des solutions est obtenue en écrivant jku sous la forme trigonométrique, ce qui donne :

z_k = 2 \sqrt{\frac{-p}{3}} \cos{\left(\frac13\arccos{\left(\frac{-q}{2}\sqrt{\frac{27}{-p^3}}\right)}+ \frac{2k\pi}{3}\right)} \mbox{ avec } k\in\{0,1,2\}\,

Exemples

Les trois exemples ci-dessous ne sont présentés que dans le but d'illustrer la méthode générale. Il va de soi que dans chacun de ces cas particuliers, diverses astuces spécifiques simplifieraient la résolution.

Exemple 1

Considérons par exemple l'équation x^3 = 18x + 35\, ou encore x^3 - 18x - 35 = 0\, . Ici, le coefficient de x^2\, est nul donc le changement de variable (en fait superflu) serait z=x\, . On a p = - 18\, et q = - 35\, , donc : u^3v^3 = {18^3 \over 27} = 216\, et u^3 + v^3 = 35\, donc u^3\, et v^3\, sont racines de l'équation X^2 - 35X + 216 = 0\, , dont les racines sont 27 et 8. Donc u et v valent 3 et 2 et la solution cherchée est x_0=z_0 = u + v = 5\, .

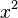
Si on se place dans \mathbb C , alors les autres racines sont u = 3\,j\, et v = 2\,j^2\, , où j = \exp\left(\frac{2i\pi}{3}\right) , ou bien u = 3j^2\, et v = 2j\, . On obtient donc comme autres racines :

z_1 = 3j + 2j^2 = - {5 \over 2} + i{\sqrt{3} \over 2}
z_2 = 3j^2 + 2j = - {5 \over 2} - i{\sqrt{3} \over 2}

Exemple 2

Soit à résoudre l'équation :

6x^3-6x^2+12x+7=0\, .

Posons x = z + \frac{1}{3} . On obtient en remplaçant et en développant :

54z^3+90z+95 = 0\, .

Posons alors z = u + v. On obtient 54(u + v)3 + 90(u + v) + 95 = 0, qui s'écrit :

54(u^3+v^3)+(162uv+90)(u+v)+95=0\,

La condition de simplification sera donc 162uv + 90 = 0, c’est-à-dire uv = -\frac{5}{9} . On a donc :

u^3+v^3 = -\frac{95}{54},\quad u^3v^3 = -\frac{125}{729} .

u3 et v3 sont donc les racines de l'équation :

X^2 + \frac{95}{54}X -\frac{125}{729} = 0

Les deux racines de cette équation sont u^3 = \frac{5}{2\cdot 27} , v^3 = -\frac{50}{27} . Les trois couples (u,v) vérifiant uv = -\frac{5}{9} sont donc :

u_0 = \frac{1}{3}\sqrt[3]{\frac{5}{2}} et v_0 = -\frac{1}{3}\sqrt[3]{50}

u_1 = \frac{j}{3}\sqrt[3]{\frac{5}{2}} et v_1 = -\frac{j^2}{3}\sqrt[3]{50}

u_2 = \frac{j^2}{3}\sqrt[3]{\frac{5}{2}} et v_2 = -\frac{j}{3}\sqrt[3]{50}

En reportant dans z = u + v on obtient :

z_0 = \frac{1}{3}\sqrt[3]{\frac{5}{2}} - \frac{1}{3}\sqrt[3]{50}

z_1 = \frac{j}{3}\sqrt[3]{\frac{5}{2}} - \frac{j^2}{3}\sqrt[3]{50}

z_2 = \frac{j^2}{3}\sqrt[3]{\frac{5}{2}} - \frac{j}{3}\sqrt[3]{50}

Et en reportant dans x = z + \frac{1}{3} on obtient finalement les trois solutions de l'équation que l'on s'était donné de résoudre :

x_0 = \frac13\left(\sqrt[3]{\frac52} - \sqrt[3]{50} + 1\right)

x_1 = \frac13\left(j\sqrt[3]{\frac52} - j^2\sqrt[3]{50} + 1\right)

x_2 = \frac13\left(j^2\sqrt[3]{\frac52} - j\sqrt[3]{50} + 1\right)

Exemple 3

Considérons l'équation x^3-6x^2+9x-1 = 0\, .

Par translation P(x) = P(z+2) = z^3-3z+1\, . Posons alors z = u + v\, .

On obtient (u + v)3 − 3(u + v) + 1 = 0, qui s'écrit :

u3 + v3 + (3uv − 3)(u + v) + 1 = 0

La condition de simplification sera donc 3uv − 3 = 0, c’est-à-dire :

uv = 1\, .

On a donc :

u^3+v^3 = -1,\qquad u^3v^3 = 1 .

u3 et v3 sont donc les racines de l'équation :

X^2 + X + 1 = 0\, .

Les deux racines de cette équation sont :

u^3 = \frac{-1+i\sqrt{3}}{2} = e^{\frac{2i\pi}{3}}= j,\qquad v^3 = \frac{-1-i\sqrt{3}}{2} = e^{\frac{-2i\pi}{3}}= j^2.

Les trois couples (u,v) vérifiant uv = 1\, sont donc :

u_0 = e^{\frac{2i\pi}{9}},\qquad v_0 = e^{\frac{-2i\pi}{9}},
u_1 = je^{\frac{2i\pi}{9}},\qquad v_1 = j^2{{e}}^{\frac{-2i\pi}{9}},
u_2 = j^2{{e}}^{\frac{2i\pi}{9}},\qquad v_2 = je^{\frac{-2i\pi}{9}}.

En reportant dans z = u + v on obtient :

z_0 = e^{\frac{2i\pi}{9}} + e^{\frac{-2i\pi}{9}} = 2\cos\left(\frac{2\pi}{9}\right) ,
z_1 = je^{\frac{2i\pi}{9}} + j^2{{e}}^{\frac{-2i\pi}{9}}= 2\cos\left(\frac{8\pi}{9}\right),
z_2 = j^2{{e}}^{\frac{2i\pi}{9}} + je^{\frac{-2i\pi}{9}}= 2\cos\left(\frac{4\pi}{9}\right),

d'où les solutions x_k=z_k+2\, .

Principe de la méthode
- Introduction - Formules de Cardan - Exemples - Principe de la méthode - Remarque historique
miniature
Des mouches dans la station spatiale chinoise Tiangong 🛰️
miniature
Cette main-robot nanométrique est capable de saisir des virus (exemple avec la COVID-19) 🖐️
miniature
Une étoile dévorée à pleine vitesse par... un trou noir ? 🌟
miniature
Cette astuce simple réduit la consommation d'alcool... des femmes 🍷
miniature
Découverte: la lumière transforme un isolant en métal 💡
miniature
Cet aliment à bannir nourrit les cancers 🍽️
miniature
Cette tablette de 3000 ans dévoile une écriture jusqu'alors inconnue ✍️
miniature
Découverte d'une chimie des océans refroidissant le climat 🌊
miniature
Le télescope James Webb, poussé à ses limites, découvre ces structures incroyablement anciennes 🔭
miniature
Le rôle surprenant de la grossesse contre la grippe A 🦠
miniature
Découverte d'une nouvelle espèce éteinte grâce à... un accélérateur de particules ⚛️
miniature
Une avancée prometteuse pour le déploiement des batteries sodium-ion 🔋
miniature
Voici comment et pourquoi le risque de cancer augmente... puis diminue avec l'âge 🧬
miniature
Le Soleil bientôt en "zone de combat": une période de turbulences extrêmes ☀️
miniature
1
Les rhumatismes plus douloureux par temps humide: vrai ou faux ? 🌧️
miniature
Ce nouveau type de moteur repousse les limites du vol supersonique ✈️
miniature
Poster sur les réseaux sociaux peut nuire à votre santé mentale 🧠
miniature
Une super-Terre entre Mars et Jupiter ? 🌎
miniature
Découverte impressionnante d'un fossile de crocodile géant 🐊
miniature
1
Cet accident en laboratoire pourrait transformer drastiquement la mémoire numérique ⚡
miniature
1
Un virage technologique révèle l'impact du diabète gestationnel 🩺
miniature
Insolite: ces loups butinent des fleurs ! Des grands carnivores pollinisateurs ? 🌼
miniature
1
Ce fin gilet robotisé soulage les tâches répétitives 🦾
miniature
Les équations d'Einstein invalidées ? 👀
miniature
Ce tatouage électronique se connecte à votre cerveau 🧠
miniature
Cette IA de Google prédit la météo mieux que jamais, et sur 15 jours ! 🌦️
miniature
Des plats au bœuf... sans bœuf ? 🥩
miniature
2
Ce moteur de recherche d'un nouveau genre bouscule nos habitudes 🔍
miniature
Pourquoi les cheveux bouclent-ils en fonction de la météo ? 🌦️
miniature
Découverte: d'autres univers plus propices à la vie que le notre 👽
miniature
Ces sons urbains qui minent notre santé mentale 🚗
miniature
La testostérone impacte-t-elle vraiment le désir sexuel des hommes ? 🔥
miniature
Des microalgues éliminent les métaux lourds: voici comment 🧪
miniature
1
Et voici un qubit mécanique ! 🖥️
miniature
Les lentilles de contact sont-elles vraiment sans danger ? 👁️
miniature
Dans la course à l'IA générative, Google lance son générateur de vidéos 🎥
miniature
4
Une zone oubliée du cerveau permet aux paralysés de marcher à nouveau 🧠
miniature
Cette astuce quotidienne ajoute 11 ans à votre vie 🕒
miniature
Révolutions, migrations des européens... les éruptions volcaniques ont influencé l'histoire 🌋
miniature
Soit l'énergie noire n'est pas constante, soit une seconde force inconnue est à l'œuvre... 🌀
miniature
Voici pourquoi l'alcool peut rendre agressif 🥂
miniature
Expérience inédite: ce laser projette une ombre visible 💥
miniature
Ce plat millénaire réduit significativement la graisse corporelle 🍽️
miniature
Les scientifiques trompés ? La Voie Lactée n'est PAS comme les autres galaxies 🔭
miniature
Pourquoi ce que pensent les autres de nous nous fait tant ruminer ? 🧠
miniature
De la vie découverte sur un échantillon de l'astéroïde Ryugu (oups) 👽
miniature
2
Des anomalies incompréhensibles de températures détectées simultanément presque partout sur Terre 🌡️
miniature
Cette planète, trop jeune pour exister, bouscule les lois de l'astronomie 🪐
miniature
Une montagne d'or découverte en Chine ⛏️
miniature
Cette simulation de l'Univers est totalement vertigineuse 🌀
Page générée en 0.347 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise