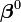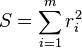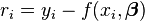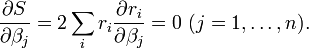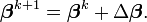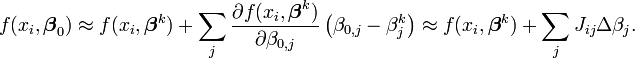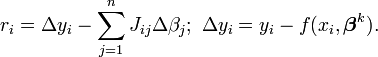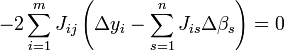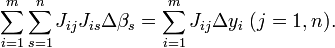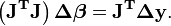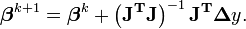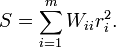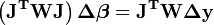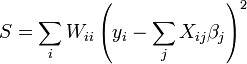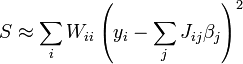Moindres carrés non linéaires - Définition

Introduction

Les moindres carrés non linéaires est une forme des moindres carrés spécialisée dans l'estimation d'un modèle non linéaire en n paramètres à partir de m observations (m > n). Une façon d'estimer ce genre de problème est de considérer des itérations successives se basant sur une version linéarisée du modèle initial.

La théorie

Considérons un jeu de m couples d'observations, et une fonction de régression du type . Cette fonction dépend des explicatives x mais aussi du vecteur des n paramètres avec On souhaite trouver le vecteur de paramètres qui ajuste au mieux les données, au sens des moindres carrés:

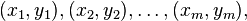
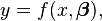
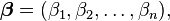
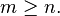
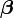
est minimisée en , où les résidus r_i sont donnés par

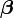
pour

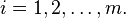
Le minimum de la somme des carrés des résidus S est atteint lorsque le Gradient s'annule (condition nécessaire). Puisque le problème est formulé avec n paramètres, il y a donc n équations normales:

Dans un système non linéaire, les dérivées dépendent aussi bien des variables explicatives que des paramètres: il faut donc renoncer à résoudre les équations normales aussi simplement que dans le cas linéaire. On a alors recours à une résolution numérique, à l'aide d'un procédé itératif

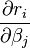
qui fournit des approximations successives de plus en plus proches de la vraie valeur (inconnue) des paramètres, .

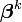
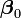
À chaque itération, le modèle initial est linéarisé par un développement de Taylor autour de comme suit:

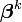
La Matrice jacobienne, J, dépend des données et de l'approximation en cours, aussi change-t-elle d'une itération à l'autre. Ainsi, en terme du modèle linéarisé, et les résidus sont donnés par

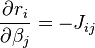
Les équations normales deviennent

ou encore

Matriciellement, on en arrive à

La linéarisation permet donc d'écrire:

Il faut remarquer que l'ensemble du terme de droite dépend seulement de l'itération en cours, à savoir , et permet donc de trouver la prochaine itération .

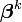
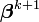
On peut aisément généraliser l'approche précédente en considérant une somme pondérée des carrés des résidus

Idéalement, chaque élément de la matrice diagonale de pondération W devrait être égal à l'inverse de la variance de l'observation Les équations normales deviennent alors

ce qui procure la base de l'algorithme d'optimisation de Gauss-Newton.

Différences entre les moindres carrés linéaires et non-linéaires

Il y a de nombreuses divergences entre les moindres carrés linéaires (MCL) et non-linéaires (MCN):

• Les MCN est un procédé itératif, qui nécessite donc un point de départ et des critères d'arrêt. Les MCL sont directs (algèbre linéaire);
• Les MCN nécessitent de calculer la matrice jacobienne (dérivées premières). Une expression analytique peut être compliquée à obtenir: si c'est le cas, une différentiation numérique s'impose;
• La divergence est un problème courant des MCN: en effet, il n'est pas rare de voir augmenter la fonction objectif (somme des carrés des résidus) d'une itération à l'autre. Cela peut être dû au manque de précision de l'approximation linéaire par le développement de Taylor;
• Pour les MCL, la solution est unique mais pas pour les MCN: plusieurs minima (locaux) peuvent exister.

Interprétation géométrique

Dans le cas des moindres carrés linéaires, la fonction objectif S est une fonction quadratique des paramètres

Lorsqu'il y a un seul paramètre à estimer β, la fonction S est une parabole en β. Pour deux paramètres ou plus, le contour de S est constitué d'ellipses concentriques, à condition que la matrice est définie positive. Le minimum, atteint pour la valeur optimale des paramètres, est le centre de ces ellipses concentriques.

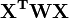
Dans le cas non linéaire, le contour en ellipses concentriques n'est vrai qu'au voisinage du minimum, puisque dans ce cas l'approximation linéaire de Taylor s'avère être une bonne approximation de la fonction objectif.

Plus les paramètres s'éloignent de leur valeur optimale, plus le contour dévie de sa forme ellipsoïdale. Ceci signifie qu'il est essentiel de choisir l'approximation initiale du procédé itératif proche des valeurs optimales, qui sont par définition inconnues.