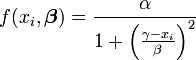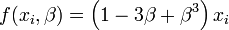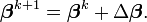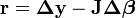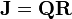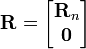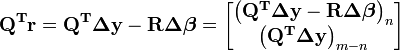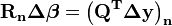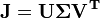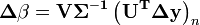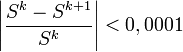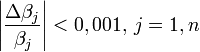Moindres carrés non linéaires - Définition

Minimums multiples

On peut trouver plusieurs minimums de S dans certaines circonstances:

• Un paramètre intervenant à une certaine puissance. Par exemple, pour ajuster des données à une courbe de Lorentz:

Il y a alors deux solution pour le paramètre β: ainsi que donnent la même valeur optimale de la fonction critère;

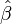
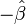
• Deux paramètres peuvent s'interchanger sans changer le critère. Par exemple, cela survient lorsqu'on rencontre le produit de deux paramètres: ainsi αβ donnera la même chose que βα;
• Un paramètre intervient dans une fonction périodique, comme par exemple dans . Dans ce cas, donne la même valeur critère.

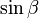
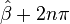
Tous les minimums multiples ne donnent pas la même valeur de la fonction objectif. Un autre problème concerne les minimums locaux. Par exemple, dans le modèle

il y a un minimum local en = 1 et un minimum global en = -3.

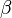
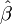
Pour être certain d'avoir obtenu un minimum global, il est souhaitable de recommencer la procédure de minimisation en changeant le point de départ. Quand on obtient le même résultat quel que soit le point de départ, on peut alors penser obtenir un minimum global.

L'existence de minimums multiples a une conséquence importante: la fonction objectif admet une valeur maximum quelque part entre les deux minimums. Les équations normales en ce maximum fait intervenir des matrices non définies positives. Une telle situation est à proscrire, en particulier comme initialisation du procédé itératif. Par exemple, pour le cas de l'ajustement du modèle de Lorentz, le cas β = 0 est à éviter.

Astuces calculatoires

Choix du vecteur d'incrément

Dans le procédé itératif

il est impératif de se prémunir contre la divergence. Plusieurs astuces concernant le choix de peuvent être considérées:

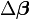
• changer sa norme sans pour autant changer sa direction. On peut alors introduire une proportion f (entre 0 et 1) et amender le procédé itératif en . Par exemple, on peut diviser par deux la valeur de f jusqu'à observer une réelle diminution de la fonction objectif. On peut aussi rechercher la valeur de f par Recherche linéaire: pour une grille de valeurs de f, on cherche la valeur de f provoquant la diminution la plus importante de S. Mais une telle méthode est couteuse en calculs, car il faut à chaque fois re-calculer la fonction objectif;
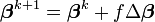
• si la direction de l'incrément est trop éloigné de sa direction "optimale" et que la méthode précédente échoue, il faudra peut-être changer légèrement la direction du vecteur d'incrément . Pour cela, les équations normales sont transformées en , où λ est le paramètre de Marquardt et I la matrice identité. On consultera avec profit la page consacrée à la méthode de Levenberg-Marquardt.

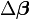
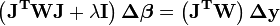
Décompositions

QR

Le minimum de la somme des carrés des résidus peut se trouver sans former les équations normales. Les résidus du modèle linéarisé s'écrivent

La jacobienne fait l'objet d'une décomposition orthogonale, comme par exemple la Décomposition QR:

où Q est une matrice orthogonale et où R est une matrice , partitionnée en un bloc , de dimension , et en un bloc nul, de dimension zero block. De plus, est triangulaire supérieure.

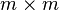
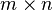
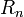
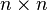
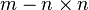
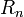
Le vecteur de résidu est pré-multiplié par .

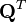
La somme des carrés reste inchangée puisque . Le minimum de S est atteint lorsque le bloc supérieur est nul. Par conséquent, le vecteur d'incrément recherché se trouve en résolvant

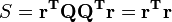
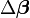
La résolution est facile d'accès car la matrice R a été prise triangulaire supérieure.

Décomposition en valeurs singulières

Une variante de la méthode précédente fait intervenir la Décomposition en valeurs singulières, dans laquelle R est diagonalisée:

où est orthogonal, est une matrice diagonale de valeurs singulières et est la matrice orthogonale des vecteurs propres de . Dans cette configuration, l'incrément est donné par

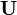
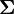
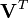
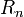
La relative simplicité de cette expression est très utile dans l'analyse théorique des moindres carrés. Cette méthode est largement détaillée dans Lawson et Hanson..

Critères de convergence

Le critère de convergence le plus immédiat est que la somme des carrés ne doit pas décroître d'une itération à l'autre. Ce critère est souvent difficile à implémenter. Aussi, on préfère le critère de convergence suivant

Évidemment, la valeur 0,0001 est arbitraire et doit être changée. En particulier, il faudra augmenter cette valeur lorsque les erreurs expérimentales sont importantes. Un critère alternatif est

Là encore, la valeur numérique est arbitraire.