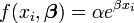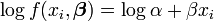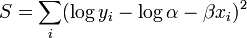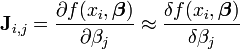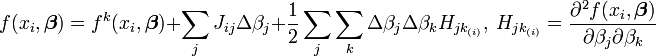Moindres carrés non linéaires - Définition

Autres méthodes

Linéarisation

Un modèle non linéaire peut parfois se transformer en modèle linéaire. Par exemple, lorsque le modèle est une simple fonction exponentielle,

on peut obtenir un modèle linéaire par transformation logarithmique.

La somme des carrés devient

Toutefois, si on n'a aucun renseignement sur la structure des aléas, cette transformation peut être problématique: de toute évidence, les erreurs expérimentales sur y ne sont pas les mêmes que sur log y. Estimer le modèle initial et celui linéarisé donnera des estimations différentes et des variances estimées. En pratique, le modèle exponentiel s'estime dans une procédure à part.

Quelques ajustements

On peut considérer quelques ajustements

• Calcul de la matrice jacobienne par approximation numérique. Dans certains modèles, obtenir des dérivées analytiques peut s'avérer délicat. On doit avoir recours à une approximation numérique de la jacobienne; par exemple, l'approximation de son entrée (i,j) est:

Cette approximation s'obtient par le calcul de pour et . L'incrément, , doit être choisi ni trop grand ni trop petit (afin d'éviter les erreurs d'arrondi);

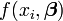
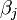
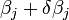
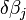
• L'inclusion des dérivées secondes dans le développement de Taylor. On obtient la méthode classique de Newton.

La matrice H est la Matrice hessienne. Bien que présentant de bien meilleures propriétés de convergence près de l'optimum, ce modèle se comporte mal quand les paramètres sont loin de leur valeur optimale. Le calcul de la Hessienne ajoute à la complexité de l'algorithme. Cette méthode n'est pas utilisée en général;

• On peut remplacer l'algorithme de Newton par un algorithme de pseudo-Newton, où on calcule numériquement la hessienne par approximations successives. C'est l'algorithme de Davidon-Fletcher-Powell (DFP);