Plan d'expérience - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
On nomme plan d'expérience la suite ordonnée d'essais d'une expérimentation, chacune permettant d'acquérir de nouvelles connaissances en contrôlant un ou plusieurs paramètres d'entrée pour obtenir des résultats validant un modèle avec une bonne économie (nombre d'essais le plus faible possible, par exemple).
Un exemple classique est le « plan en étoile » où en partant d'un jeu de valeurs choisi pour les paramètres d'une expérience centrale, on complète celle-ci par des expériences où chaque fois un seul des facteurs varie « toutes choses égales par ailleurs ».
Un type de plan plus efficace est le « plan factoriel » consistant à choisir des valeurs pour chacun des facteurs en variant simultanément tous les facteurs (de façon exhaustive ou non). Le nombre d'essais peut alors devenir très grand (explosion combinatoire).
Cet article comporte des exemples illustrant la notion de plan d'expériences et expose des cas à la fois simples et fréquents.
Position du problème
Supposons que nous désirions savoir si la proportion de boules noires d'une urne est supérieure à 5%, l'urne contenant 1000 boules. Nous partons avec l'idée d'en tirer 100 dans l'espoir d'avoir une bonne approximation de la proportion.
- Si au cours du tirage, nous ramenons 51 boules noires, celui-ci peut être arrêté immédiatement : le poursuivre n'aurait pas de sens, puisqu'avec 51 boules noires sur 1000 une proportion supérieure à 5% est maintenant certaine.
- On peut raffiner encore en remarquant que la probabilité de tirer par exemple 5 boules noires dans les 5 premiers tirages ramène à 0,3 x 10-6 la probabilité que la proportion de boules noires soit inférieure à 5%.
- Dans la pratique, le calcul permet d'établir des règles strictes indiquant en fonction des résultats à quel moment le tirage doit s'arrêter - avec décision prise dans un sens ou dans l'autre - ou s'il doit être poursuivi.
Un plan d'expérience permet donc de réduire le nombre d'essais à ce qui est strictement nécessaire pour prendre une décision, ce qui peut sauver du temps, de l'argent et des vies.
C'est un plan d'expérience de ce type qui a permis d'arrêter en cours de route une expérience visant à déterminer si l'aspirine avait un effet de prévention sur les crises cardiaques, les résultats établissant sans ambiguïté que c'était le cas (réduction de 25% des risques). Continuer l'expérimentation serait revenu dans ces conditions à priver jusqu'à la date initialement prévue les malades du lot-témoin d'accès à l'aspirine, ce qui aurait pu coûter la vie à certains d'entre eux.
Limites des plans expérimentaux exhaustifs
Supposons que l'on soit en présence d'un processus qui dépende de 3 facteurs A, B et C qui ont chacun leur domaine de définition (discret) {ai | i = 1,..,l} , {bj | j = 1,...,m} , {ck | k = 1,...,n}.
Une approche systématique consisterait à effectuer toutes les expériences possibles du processus en faisant varier chacun des paramètres dans son domaine de définition:
Expérience 1: {a1,b1,c1}
Expérience 2:{a2,b1,c1}
Expérience 3:{a3,b1,c1}
Expérience l


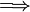
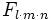
Le nombre d'expériences nécessaires, qui est égal au produit l


En sciences appliquées (plans expérimentaux)
Il existe de nombreux processus qu'on sait dépendre d'un grand nombre de paramètres externes (on parle de facteurs) mais sans que l'on en ait des modèles analytiques.
Lorsque l'on est intéressé de connaître la dépendance d'une variable de sortie F d'un tel processus, on se trouve confronté à plusieurs difficultés :
- Quels sont les facteurs les plus influents ?
- Existe-t-il des interactions entre les facteurs (corrélations) ?
- Peut-on linéariser le processus en fonction de ces facteurs et le modèle ainsi obtenu est-il prédictif ?
- Comment minimiser le nombre de points de mesure du processus pour obtenir le maximum d'informations ?
- Existe-t-il des biais dans les résultats des mesures ?
La méthode du plan d'expérience répond à ces questions et peut ainsi être appliquée dans de nombreux processus qui vont par exemple des essais cliniques à l'évaluation de la qualité des processus industriels les plus complexes.
On peut ainsi pour l'industrie poser cette nouvelle définition : Un plan d'expériences est une suite d’essais rigoureusement organisés, afin de déterminer avec un minimum d’essais et un maximum de précision, l’influence respectives des différents paramètres de conception ou de fabrication d’un produit, afin d’en optimiser les performances.
En sciences humaines
Les symboles utilisés
- <...> = Emboîté, c'est-à-dire qu'il y a un groupe par modalité !
- * ... = Croisé, c'est-à-dire qu'il n'y a qu'un seul groupe pour toutes les modalités.
- S = Signifie sujet.
- S
= Signifie qu'il y a 20 sujets (car 10 sujets x 2 modalités) - S*M = Signifie qu'il y a 10 sujets
- M = M est le symbole d'une VI (Variable Indépendante), et 2 en indice, indique le nombre de modalités.
Plan monofactoriel
On peut avoir deux types de plan monofactoriel :
| Méthode 1 | Méthode 2 | |
|---|---|---|
| Type de plan | Emboîté | Croisé |
| Type de groupe | Groupes indépendants | Groupes appareillés |
| Formule | S | S*M |
| Nombre de données | 20 données pour 20 sujets 10 sujets pour M1 et 10 pour M2 | 20 données pour 10 sujets les 10 sujets passent M1 et M2 |
| Problème | Il est difficile d'avoir 2 groupes réellement équivalents | Il y a des interférences d'une activité à l'autre |
Plan multifactoriel
On aura ici, au moins 2 VI à tester en même temps. On peut avoir trois types de plan multifactoriel :
| Méthode 1 | Méthode 2 | Méthode 3 | |
|---|---|---|---|
| Type de plan | Emboîté complet | Croisé complet | Mixte ou quasi complet |
| Type de groupe | Un Groupe de sujets par groupe expérimental | Chaque sujet rencontre toutes les conditions expérimentales | On a deux groupes emboîtés, qui passe chacun toutes les conditions |
| Formule | S | S*M*R | S |
| Nombre de données | 60 données pour 60 sujets | 60 données pour 10 sujets | 60 données pour 20 sujets |
| Problème | Il est difficile d'avoir des groupes réellement équivalents + Besoin de beaucoup de sujets | Peut être fatiguant pour les sujets + Il va y avoir un effet d'une condition à l'autre | . |

















































