Polynôme de Hurwitz - Définition

Introduction

Un polynôme à coefficients réels, de degré n, est appelé polynôme de Hurwitz si ses n racines complexes sont toutes à partie réelle négative.

On montre aisément que nécessairement, tous les coefficients du polynôme sont de même signe, et donc sans restreindre la généralité, on prend le terme constant T₀ égal à 1 en physique.

Résultats pour n<5

n=2 : pas d'autre condition (évident pour un physicien habitué au circuit RLC).

n=3 : rajouter : ET T₂.T₁ − T₃.T₀ > 0

n=4 : rajouter : ET

Remarque : pour un physicien, les coefficientsT_n sont des constantes de temps à la puissance n. Il pourra aisément contrôler l'homogénéité des formules.

Le cas n = 3 se retient aisément par des considérations énergétiques (voir l'article filtre électrique linéaire).

Le cas n=4 se retient mnémotechniquement aisément grâce au cas n=3 : effectivement si T4 est quasi-nul, on devait retrouver n=3 . Par contre, il faut connaître la situation de 2 oscillateurs couplés avec injection de puissance, pour intuiter aisément l'inéquation T₂.T₁ / T₃.T₀ > 1 + k.(T₄ / T₀).(T₁ / T₃)², k=1 .

Au-delà, il vaut mieux traiter la question par l'algorithme des tableaux de Routh. Néanmoins, une remarque de pertinence : si P(x) est de Hurwitz, x^n .P(1/x) est de Hurwitz : les conditions sont donc « symétriques » sur les coefficients.

Par exemple, le cas n= 5 se retient assez aisément: il y a deux inégalités:

A: = (T₄.T₃ − T₅.T₂) > 0

évidemment et

B² − A.C < 0

avec B: = (T₄.T₁ − T₅.T₀)

et

C: = (T₂.T₁ − T₃.T₀)

Cas général : les tableaux de Routh et critère de Routh-Hurwitz

Le tableau de Routh est un critère de stabilité utilisé en automatique. Il permet de déterminer, au regard du dénominateur de la fonction de transfert en boucle fermée, si le système bouclé, représenté par cette fonction, est stable ou non (cf stabilité EBSB).

Soit s la variable de la fonction de transfert. Le dénominateur s'écrit sous la forme d'un polynôme en s :

a_nsⁿ + a_{n − 1}s^{n − 1} + ... + a₀

• Condition nécessaire :
  • Tous les coefficients a_i doivent être non nuls
  • Tous les coefficients a_i doivent être de même signe

Rem : autre manière de dire : ao = 1 et tous les coefficients strictement positifs.

Si ces 2 conditions ne sont pas réunies, le système est instable.

Pour déterminer en plus la condition suffisante, il nous faut dresser le tableau de Routh.

La 1e ligne du tableau, indexée par sⁿ, comporte les coefficients a_n, a_{n − 2},....

La 2e ligne du tableau, indexée par s^{n − 1}, comporte les coefficients a_{n − 1}, a_{n − 3},...

Puis pour les autres lignes, on complète de la manière suivante :

1e colonne de la 3e ligne :

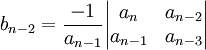
2e colonne de la 3e ligne :

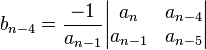
ect.... (si on ne peut pas compléter une case, on y met un zéro)

ce qui nous donne le tableau suivant :

Tableau de Routh

sn	an	an − 2	an − 4
sn − 1	an − 1	an − 3	an − 5
sn − 2			...
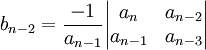
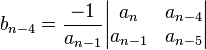
sn − 3		...	...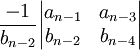

• Condition nécessaire et suffisante :

Si tous les coefficients de la 1re colonne du tableau sont tous non nuls et de même signe, alors le système bouclé est stable.

Remarque : la condition nécessaire et suffisante de stabilité pour un système du 2e ordre est que tous les coefficents soient de même signe (on obtient simplement ce résultat en appliquant le critère de Routh).

Exemple : af''(t) + bf(t) = 0 avec a > 0

si b > 0 alors les coefficents sont de même signe donc le système est stable. En effet, la solution f(t) est :

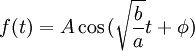
f(t) est alors bornée comme l'entrée (ici 0) donc le système est stable.

si b < 0, le système est instable. En effet, la solution est :

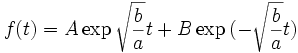
qui diverge lorsque t tend vers l'infini.