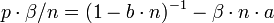Pression cinétique - Définition

Longueur de Loschmidt

La longueur de Loschmidt est la distance moyenne séparant deux molécules dans les conditions normales de pression et de température ; elle est définie comme étant la racine cubique du volume libre moyen autour d'une molécule. Cette longueur est indépendante du gaz parfait considéré, et vaut

d = 333 pm.

Voir l'article Gaz parfait.

Équation d'état du viriel

Le paragraphe correction de covolume a indiqué :

,

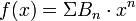
dans le cas d'un gaz de boules dures, les calculs ultérieurs montreront que :

• f(x) = 1 + 4x + 10x² + 18,3648x³ + 28,24x⁴ + 39,53x⁵ + ...

Les 4 premiers termes sont analytiques, les deux suivants sont numériques (calcul d'intégrales par la méthode de Monte-Carlo).

Or la série suivante :

1 + 4x + 10x² + 18x³ + 28x⁴ + 40x⁵ + 54x⁶ + 70x⁷ + O(x⁸),x,8

montre que : est une fonction "bon-candidat" simple , pour un gaz de boules dures.

Or cela indique une asymptote pour x = 1, alors que, évidemment, on ne saurait dépasser la compacité maximale de Pi/sqrt(18). Cela limite la portée de ce calcul et l'on verra comment l'améliorer dans un paragraphe ultérieur.

calcul de B2 = 4

calcul de B3 = 10

calcul de B4 = 18,36.

calcul de Bn

expression de B2, B3 et B4

Le calcul de la fonction de partition(en mécanique classique) donne les résultats suivants :

La pression interne de Van der Waals

Van der Waals, s'appuyant sur les travaux de Laplace, a compris le rôle que jouait l'attraction entre 2 particules du gaz (attraction qui porte aujourd'hui son nom). En moyenne, une particule située à grande distance de la paroi ne ressent qu'une force moyenne NULLE. Par contre, une particule allant vers la paroi est décélérée par cette attraction, multiple de la densité : donc l'énergie cinétique d'impact sera réduite d'un facteur F.L.N/V. Et pour la pression due à l'ensemble des particules, il y aura donc une réduction d'un facteur (N/V)^2:

L'ensemble de ces considérations amenèrent Van der Waals à sa célèbre équation :

ou encore :

Il ne faut pas croire la pression interne comme négligeable, car elle varie considérablement. Donnons-en une évaluation :

Soit de l'eau liquide en équilibre à 473K avec sa vapeur :pour le liquide NkT/V est très grande : 55000/22.4 (473/373)~2000 bars , donc la pression interne, 2000-1, aussi . mais pour la vapeur , elle sera environ 1/10^6 fois plus faible , soit 1/1000 bar et donc négligeable.

Autres équations d'état

Percus-Yevick , Redlich-Kwong , facteur acentrique...