Asymptote - Définition
Le terme d'asymptote est utilisé en mathématiques pour préciser des propriétés éventuelles d'une branche infinie de courbe à accroissement tendant vers l'infinitésimal. C'est d'abord un adjectif d'étymologie grecque qui peut qualifier une droite, un cercle, un point ... dont une courbe plus complexe peut se rapprocher. C'est aussi devenu un nom féminin synonyme de droite asymptote.
L'étude du comportement asymptotique est particulièrement développé dans les études de fonctions. Dans le domaine scientifique, il arrive fréquemment d'étudier des fonctions dépendant du temps (évolution de populations, réaction chimique ou nucléaire, graphique de température, oscillation d'un amortisseur). Un des objectifs du chercheur est alors de connaitre l'état à la fin de l'expérience, c’est-à-dire lorsqu'un grand intervalle de temps s'est écoulé. L'objectif n'est alors pas de connaitre les variations intermédiaires mais de déterminer le comportement stable, à l'infini du phénomène mesuré. Le chercheur étudie donc le comportement asymptotique de sa fonction avec les outils que les mathématiques lui offrent.
Le projet d'une définition uniforme n'étant pas raisonnable, cet article détaillera plusieurs situations.
Courbe d'équation y = f(x)
Les asymptotes sont à rechercher lorsque x ou f(x) tend vers l'infini.
Droite asymptote
Asymptote " verticale "
La droite d'équation x = a est une asymptote " verticale " à la courbe représentative de la fonction f (en a+) si quel que soit x>a,
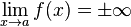
La droite d'équation x = a est asymptote " verticale " à la courbe représentative de la fonction f (en a-) si quel que soit x![]() .
.
On trouvera des asymptotes verticales en particulier lorsque la fonction f se présente sous forme d'un quotient dont le dénominateur, mais pas le numérateur, s'annule en a.
Exemples : fonction homographique, logarithme népérien, fonction tangente
Asymptote " horizontale "
La droite d'équation y = b est asymptote horizontale à la courbe d'équation y = f(x), si
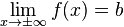
Exemples : fonction homographique, exponentielle. tangente hyperbolique
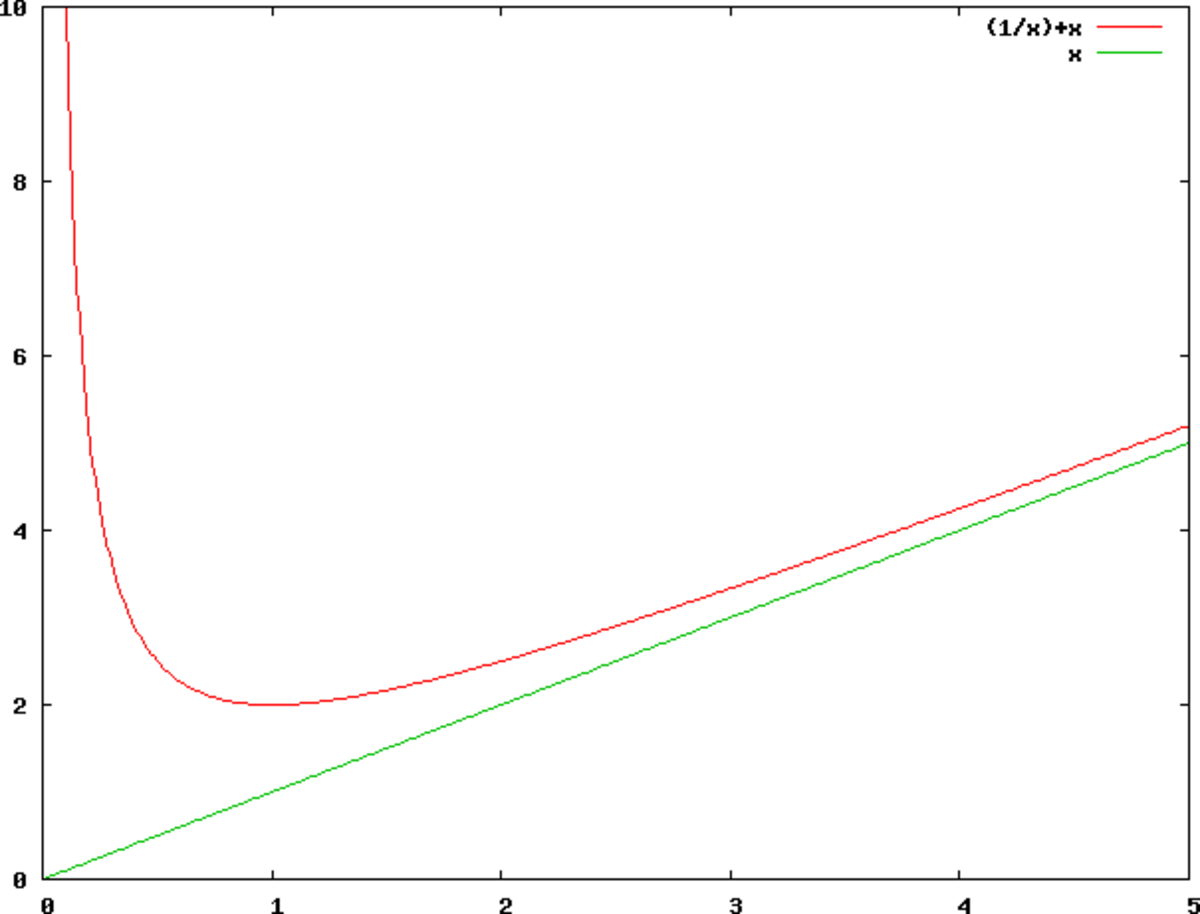
Asymptote " oblique "
La droite d'équation y = ax + b est asymptote oblique à la courbe représentative de la fonction f si
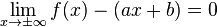
les valeurs de a et de b peuvent se retrouver à l'aide des remarques suivantes :
-
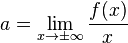
-
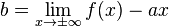
Lorsque la limite
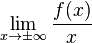
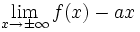
Exemples : fonction rationnelle,
Le point de vue projectif
Les trois situations précédentes n'en forment qu'une en géométrie projective, une asymptote étant une tangente à l'infini.
Courbe asymptote
La courbe d'équation y = g(x) est asymptote à la courbe d'équation y = f(x) en
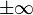
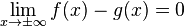
La courbe d'équation y = g(x) est asymptote à la courbe en
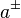
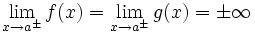
Exemple : Une courbe d'équation
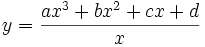
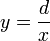
Courbe paramétrée
On cherche les asymptotes aux branches infinies de la courbe d'équation (x = x(t) ; y = y(t) ), c’est-à-dire en t0 (réel ou infini) tel que
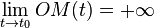
Droite asymptote horizontale
La courbe admet la droite
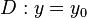
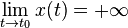
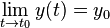
Exemple à trouver
Droite asymptote verticale
La courbe admet la droite
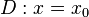
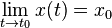
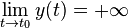
Exemple à trouver
Autre asympote
Si
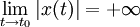
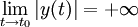
Nous cherchons donc à étudier (si elle existe), la limite l de
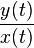
Si l est


Si l est réelle, l'asymptote est la droite d'équation y = lx
Exemple à trouver
Méthode de recherche
Méthode à proposer Exemple à trouver
Courbe d'équation polaire
On cherche les asympotes à la courbe d'équation r = ρ(θ) lorsque r ou θ tend vers l'infini
Droite asymptote
À faire
Cercle asympote
À faire
Point asymptote
À faire