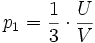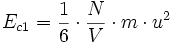Pression cinétique - Définition

Introduction

La pression cinétique, ou pression de Daniel Bernoulli (1700—1782), est la pression résultant des chocs inélastiques des particules sur la paroi thermalisée. Ce calcul de 1738 en théorie cinétique des gaz est remarquable, car il précède d'un siècle cette théorie, essentiellement initiée par Clausius en 1857.

Le résultat pour un gaz parfait monoatomique simple est :

où

• p est la pression ;
• U est l'énergie interne du système ;
• V est le volume du système.

Concrètement, la pression représente les deux tiers de l'énergie volumique (Rappel : le pascal est homogène à des joules par mètre cube).

Démonstration

il y a deux contributions : celle des particules qui s'adsorbent en impactant la paroi :

et celle identique des particules qui désorbent en prenant appui sur la paroi :

soit, si l'on appelle <u> la vitesse quadratique moyenne, une énergie cinétique

en impact, et idem en appui.

Pour la démonstration , on utilisera le théorème du viriel :

2 < E_c > + < viriel > = 0

Ici, la force moyenne dƒ sur l'ensemble des particules du gaz sur un élément dS de surface est . Sommée sur l'ensemble de la paroi S qui enclôt le gaz :

La pression p est homogène, donc sort de l'intégrale ; le reste est classique (1/3 V). Au total, le viriel est négatif bien sûr, et vaut -1/3·pV, soit

On peut aussi se rapporter à la démonstration faite dans l'article Théorie cinétique des gaz > Pression et énergie cinétique.

Corrections de covolume de Daniel Bernoulli

Dès 1738, Bernoulli avait compris le rôle de la taille des atomes : raisonnant sur un gaz à une dimension - fait de « pailles » de longueur a - il avait compris que le « volume » réel disponible pour l'ensemble des pailles était non pas la taille L du segment où elles étaient incluses, mais L - Na.

À deux dimensions, il comprenait de même que si la surface de chaque disque était s, la surface réellement disponible pour l'ensemble des disques était non pas la surface S du plateau où elles étaient encloses, mais S - 2Ns, pour S assez grand (le facteur 2 sera expliqué plus loin).

Enfin, à 3 dimensions, il avait aussi compris que le volume disponible serait inférieur à V :

pV − Nb = NkT ;

avec

.

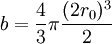
Le paramètre N b est appelé « co-volume » ou « volume résiduel ».

On appelle « compacité », et on note x, le rapport entre le volume propre des particules de rayon r₀ et le volume total. L'équation précédente peut s'écrire en série de la compacité :

.

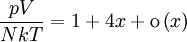
• Autre notation plus moderne :

Souvent dans les textes de mécanique statistique, on pose et (nommée densité particulaire). L'équation se note alors :

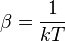
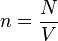
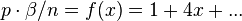
Ainsi l'étude des isothermes à basse pression permet d'évaluer ce covolume, donc le rayon r₀ des particules.

Une étude plus poussée permit à Boltzmann de calculer analytiquement les 2 termes suivants de la série :

.

On sait, avec les ordinateurs actuels, trouver les 8 premiers termes de ce développement dit du « viriel » d'un gaz modélisé par des boules dures. On sait aussi en calculer le rayon de convergence, et l'approcher par un Approximant de Padé, ce qui donne une meilleure compréhension de l'asymptote, qui n'est évidemment pas V = N b ! En effet, la compacité tend vers x = π/(18)^1/2 ~ 74%. D'ailleurs, les simulations-numériques sur computer-Argon révèlent parfois un changement de phase vers x = 60%.