Problème de la couverture exacte - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le problème de la couverture exacte est un problème d'optimisation combinatoire NP-complet qui fait partie des 21 problèmes NP-complets de Karp.
Énoncé
Étant donné un univers U d'éléments et une collection
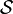
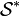
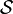
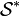
En d'autres termes, une couverture exacte est une sous-collection
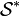
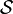
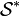
Étant donné un univers U d'éléments et une collection
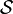
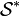
Le problème de la couverture exacte est un exemple d'un problème de satisfaction de contraintes.
Exemple 1
Soit U = {0, 1, 2, 3, 4, ...} l'univers des entiers naturels et soit
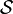
- les nombres pairs E = {0, 2, 4, 6, 8, ...};
- les nombres impairs I = {1, 3, 5, 7, 9, ...}; et
- les nombres premiers P = {2, 3, 5, 7, ...}.
Alors, la sous-collection
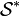
Par contre, {E, P} n'est pas une couverture exacte, puisque certains nombres naturels ne sont contenus dans aucun ensemble : par exemple, 1 est ni pair ni premier. De plus, certains nombres naturels sont contenus dans plusieurs ensembles : par exemple, 2 est et pair et premier.
Exemple 2
Soit U = {1, 2, 3, 4, 5, 6, 7} un univers de 7 éléments et soit
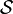
- A = {1, 4, 7};
- B = {1, 4};
- C = {4, 5, 7};
- D = {3, 5, 6};
- E = {2, 3, 6, 7}; et
- F = {2, 7}.
Alors, la sous-collection
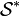
De plus, {B, D, F} est la seule couverture exacte, comme le démontre l'argument suivant : Une couverture exacte doit couvrir 1 et A et B sont les seuls ensemble contenant 1, ainsi une couverture exacte doit contenir A ou B, mais non les deux. Si une couverture exacte contient A, alors elle ne contient ni B, C, E, ou F, comme chacun de ces ensemble ont au moins un élément en commun avec A. Alors D est le seul ensemble restant qui soit une partie de la couverture exacte, mais la collection {A, D} ne couvre pas l'élément 2. En conclusion, il n'existe pas de couverture exacte contenant A. D'un autre côté, si une couverture exacte contient B, alors elle n'inclut ni A ni C, comme chacun de ces ensembles ont au moins un élément en commun avec B. Alors D est le seul ensemble restant qui contient 5, donc D doit être une partie de la couverture exacte. Si une couverture exacte contient D, alors elle ne contient pas E, comme D et E ont les éléments 3 et 6 en commun. Alors F est le seul ensemble restant qui soit une partie de la couverture exacte, et la collection {B, D, F} est vraiment une couverture exacte. Voir l'algorithme X de Knuth pour une version de cet argument basée sur une matrice.
Généralisations
Bien que le problème standard de la couverture exacte implique une collection
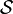
Étant donné un ensemble X, un ensemble Y, et une relation binaire R entre X et Y, une couverture exacte (généralisée) est un sous-ensemble X* de X tel que chaque élément de Y est R-1-relié à exactement un élément de X*. Ici R-1 est l'inverse de R.
En général, R-1 restreinte à Y×X* est une fonction, c.a.d., chaque élément Y est R-1-relié à exactement un élément de X* : l'unique élément de X* qui « couvre » l'élément particulier de Y.
De plus, si R est totalement gauche, c.a.d., si chaque élément de X est R-relié à au moins un élément de Y, alors R-1 restreinte à Y×X* est une fonction surjective. (La condition dans le problème généralisé que R est totalement gauche correspond à la condition dans le problème standard que chaque ensemble dans
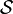
Dans la représentation matricielle du problème généralisé, la relation R est représentée par une matrice, les éléments de X sont représentés par les lignes de la matrice, et les éléments de Y sont représentés par les colonnes de la matrice. Alors, comme dans le problème standard, une couverture exacte (généralisée) est une sélection de lignes telles que chaque colonne possède 1 dans exactement une des lignes sélectionnées.
Le problème standard est un cas particulier du problème généralisé dans lequel l'ensemble X est une collection
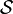
Exemple 4
La matrice dans l'exemple 3 ci-dessus peut être réinterprété pour représenter la relation binaire « est contenu dans » entre l'ensemble X = {1, 2, 3, 4, 5, 6} de 6 éléments et la collection Y = {A, B, C, D, E, F, G} de 7 ensembles :
- A = {1, 2}
- B = {5, 6}
- C = {4, 5}
- D = {1, 2, 3}
- E = {3, 4}
- F = {4, 5}
- G = {1, 3, 5, 6}
La même représentation matricielle comme dans l'exemple 3 s'applique ici, mais elle est étiquetée différemment :
-
A B C D E F G 1 1 0 0 1 0 0 1 2 1 0 0 1 0 0 0 3 0 0 0 1 1 0 1 4 0 0 1 0 1 1 0 5 0 1 1 0 0 1 1 6 0 1 0 0 0 0 1
Comme dans l'exemple 3, une solution consiste à sélectionner les 2e, 4e et 6e lignes de la matrice :
-
A B C D E F G 2 1 0 0 1 0 0 0 4 0 0 1 0 1 1 0 6 0 1 0 0 0 0 1
Mais à la différence de l'exemple 3, l'interprétation ici montre que la solution est l'ensemble des éléments X* = {2, 4, 6} tel que chaque ensemble dans Y contient exactement un élément de X* :
- A = {1, 2}
- B = {5, 6}
- C = {4, 5}
- D = {1, 2, 3}
- E = {3, 4}
- F = {4, 5}
- G = {1, 3, 5, 6}
En d'autre termes, la solution est un ensemble intersectant exact. Vraiment, les problèmes de la couverture exacte et les problèmes d'ensemble intersectant exact sont duaux l'un de l'autre, c.a.d. essentiellement les mêmes.

















































