Problème de la couverture exacte - Définition

Représentation matricielle

Si = {S₁, S₂, ..., S_m} est une collection finie de m ensembles et U = {x₁, x₂, ..., x_n} est un univers fini de n éléments, alors le problème de la couverture exacte peut être représenté comme une matrice m×n contenant seulement des 0 et des 1. La i-ème ligne de la matrice représente le i-ème ensemble S_i et la j-ème colonne de la matrice représente le j-ème élément x_j. L'entrée de la matrice dans la i-ème ligne et la j-ème colonne est 1 si l'ensemble S_i contient l'élément x_j; l'entrée est 0 sinon.

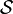
Étant donné une telle matrice, une couverture exacte est une sélection de lignes telles que chaque colonne possède un 1 dans exactement une des lignes sélectionnées.

En d'autres termes, une couverture exacte est une sélection de lignes dont la somme est une ligne qui ne contient que des 1.

Exemple 3

Si dans l'exemple 2 ci-dessus, nous représentons les 6 ensembles dans = {A, B, C, D, E, F} sous forme de lignes et les 7 éléments dans U = {1, 2, 3, 4, 5, 6, 7} sous forme de colonnes, alors le problème de la couverture exacte est représenté par la matrice 6×7 :

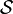
	1	2	3	4	5	6	7
A	1	0	0	1	0	0	1
B	1	0	0	1	0	0	0
C	0	0	0	1	1	0	1
D	0	0	1	0	1	1	0
E	0	1	1	0	0	1	1
F	0	1	0	0	0	0	1

Comme dans l'exemple 2, la sélection = {B, D, F} de lignes est une solution de ce problème de couverture exacte :

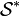
	1	2	3	4	5	6	7
B	1	0	0	1	0	0	0
D	0	0	1	0	1	1	0
F	0	1	0	0	0	0	1

Exemples plus approfondis

Beaucoup de problèmes peuvent être réduits à des problèmes de la couverture exacte, qui peuvent alors être résolus avec des techniques comme les liens dansants.

Par exemple, le problème de pavage d'une surface donnée avec des pentominos, le problème des huit reines, et la résolution des Sudokus peuvent tous être vus comme des problèmes de la couverture exacte et être résolus avec les liens dansants.

Pavage de pentominos

Le problème de pavage d'une surface donnée avec des pentominos est un exemple de problème de la couverture exacte.

Par exemple, voir le site en anglais Solving Pentomino Puzzles with Backtracking.

Le problème des huit reines

Le problème des huit reines est un exemple de problème de la couverture exacte.

Sudoku

Le problème dans les Sudokus est d'assigner une certaine quantité de nombres (ou chiffres, valeurs, symboles) aux cellules (ou carrés) dans une grille tout en satisfaisant certaines contraintes.

Dans les variantes standard d'un Sudoku 9×9, il existe quatre sortes de contraintes :

Ligne-Colonne : Chaque intersection d'une ligne et d'une colonne, i.e, chaque cellule, doit contenir exactement un nombre.

Ligne-Nombre : Chaque ligne doit contenir chacun des 9 nombres exactement une seule fois.

Colonne-Nombre : Chaque colonne doit contenir chacun des 9 nombres exactement une seule fois.

Boîte-Nombre : Chaque boîte doit contenir chacun des 9 nombres exactement une seule fois.

Bien que la première contrainte semble triviale, il est cependant nécessaire de s'assurer qu'il n'y aura qu'un seul nombre par cellule.

La résolution d'un Sudoku est un problème de la couverture exacte.

Plus précisément, résoudre un Sudoku est un problème d'ensemble intersectant, ce qui est équivalent à un problème de la couverture exacte (comme dans l'exemple 4 ci-dessus), lorsqu'il est vu comme un problème de sélection de possibilités tel que chaque ensemble de contraintes contient (i.e., est atteint par) exactement une possibilité sélectionnée. Dans la notation ci-dessus pour le problème de la couverture exacte (généralisé), X est l'ensemble des possibilités, Y est un ensemble d'ensembles de contraintes, et R est la relation binaire "est contenu dans".

Chaque assignation possible d'un nombre particulier à une cellule particulière est une possibilité (ou un candidat). Lorsque le Sudoku est joué avec un crayon et un papier, les possibilités sont souvent appelées des marques de crayon.

Dans les variantes standard d'un Sudoku 9×9, dans lequel chacune des cellules 9×9 est assignée un des 9 nombres, il y a 9×9×9 = 729 possibilités. En utilisant une notation évidente pour les lignes, colonnes et nombres, les possibilités peuvent être étiquetées comme ceci : R1C1#1, R1C1#2, …, R9C9#9.

Le fait que chaque sorte de contrainte implique exactement une chose est ce qui fait que le Sudoku est un problème d'ensemble intersectant exact. Les contraintes peuvent être représentées par les ensembles de contraintes. Le problème est de sélectionner les possibilités telles que chaque ensemble de contraintes contient (c.a.d., est atteint par) exactement une possibilité sélectionnée.

Dans les variantes standard d'un Sudoku 9×9, il existe quatre sortes d'ensembles de contraintes correspondant aux quatre sortes de contraintes :

Ligne-Colonne : Un ensemble de contraintes ligne-colonne contient toutes les possibilités pour l'intersection d'une ligne et d'une colonne particulière, i.e., pour une cellule. Par exemple, l'ensemble de contraintes pour la ligne 1 et la colonne 1, qui peut être étiquetée R1C1, contient les 9 possibilités pour la ligne 1 et la colonne 1 mais avec des nombres différents :

R1C1 = { R1C1#1, R1C1#2, R1C1#3, R1C1#4, R1C1#5, R1C1#6, R1C1#7, R1C1#8, R1C1#9 }.

Ligne-Nombre : Un ensemble de contraintes ligne-nombre contient toutes les possibilités pour une ligne particulière et un nombre. Par exemple, l'ensemble de contraintes pour la ligne 1 et le nombre 1, qui peut être étiquetée R1#1, contient les 9 possibilités pour la ligne 1 et le nombre 1 mais de différentes colonnes :

R1#1 = { R1C1#1, R1C2#1, R1C3#1, R1C4#1, R1C5#1, R1C6#1, R1C7#1, R1C8#1, R1C9#1 }.

Colonne-Nombre : Un ensemble de contraintes colonne-nombre contient toutes les possibilités pour une colonne particulière et un nombre. Par exemple, l'ensemble de contraintes pour la colonne 1 et le nombre 1, qui peut être étiquetée C1#1, contient les 9 possibilités pour la colonne 1 et le nombre 1 mais de différentes lignes :

C1#1 = { R1C1#1, R2C1#1, R3C1#1, R4C1#1, R5C1#1, R6C1#1, R7C1#1, R8C1#1, R9C1#1 }.

Boite-Nombre : Un ensemble de contraintes boite-nombre contient toutes les possibilités pour une boîte particulière et un nombre. Par exemple, l'ensemble de contraintes pour la boîte 1 (dans le coin supérieur gauche) et le nombre 1, qui peut être étiquetée B1#1, contient les 9 possibilités pour les cellules dans la boîte 1 et le nombre 1 :

B1#1 = { R1C1#1, R1C2#1, R1C3#1, R2C1#1, R2C2#1, R2C3#1, R3C1#1, R3C2#1, R3C3#1 }.

Puisqu'il existe 9 lignes, 9 colonnes, 9 boîtes et 9 nombres, il existe 9×9=81 ensembles de contraintes ligne-colonne, 9×9=81 ensembles de contraintes ligne-nombre, 9×9=81 ensembles de contraintes colonne-nombre et 9×9=81 ensembles de contraintes boîte-nombre : 81+81+81+81=324 ensembles de contraintes en tout.

En bref, les variantes standard d'un Sudoku 9×9 est un problème d'ensemble intersectant exact avec 729 possibilités et 324 ensembles de contraintes. Le problème peut donc être représenté par une matrice 729×324.

Bien qu'il soit difficile de présenter la matrice 729×324 entière, la nature générale de la matrice peut être vue à partir de plusieurs captures :

Contraintes Ligne-Colonne R1 C1 R1 C2 … R1C1#1 1 0 … R1C1#2 1 0 … R1C1#3 1 0 … R1C1#4 1 0 … R1C1#5 1 0 … R1C1#6 1 0 … R1C1#7 1 0 … R1C1#8 1 0 … R1C1#9 1 0 … R1C2#1 0 1 … R1C2#2 0 1 … R1C2#3 0 1 … R1C2#4 0 1 … R1C2#5 0 1 … R1C2#6 0 1 … R1C2#7 0 1 … R1C2#8 0 1 … R1C2#9 0 1 … … … … …

Contraintes Ligne-Nombre R1 #1 R1 #2 … R1C1#1 1 0 … R1C1#2 0 1 … … … … … R1C2#1 1 0 … R1C2#2 0 1 … … … … … R1C3#1 1 0 … R1C3#2 0 1 … … … … … R1C4#1 1 0 … R1C4#2 0 1 … … … … … R1C5#1 1 0 … R1C5#2 0 1 … … … … … R1C6#1 1 0 … R1C6#2 0 1 … … … … … R1C7#1 1 0 … R1C7#2 0 1 … … … … … R1C8#1 1 0 … R1C8#2 0 1 … … … … … R1C9#1 1 0 … R1C9#2 0 1 … … … … …

Contraintes Colonne-Nombre C1 #1 C1 #2 … R1C1#1 1 0 … R1C1#2 0 1 … … … … … R2C1#1 1 0 … R2C1#2 0 1 … … … … … R3C1#1 1 0 … R3C1#2 0 1 … … … … … R4C1#1 1 0 … R4C1#2 0 1 … … … … … R5C1#1 1 0 … R5C1#2 0 1 … … … … … R6C1#1 1 0 … R6C1#2 0 1 … … … … … R7C1#1 1 0 … R7C1#2 0 1 … … … … … R8C1#1 1 0 … R8C1#2 0 1 … … … … … R9C1#1 1 0 … R9C1#2 0 1 … … … … …

Contraintes Boîte-Nombre B1 #1 B1 #2 … R1C1#1 1 0 … R1C1#2 0 1 … … … … … R1C2#1 1 0 … R1C2#2 0 1 … … … … … R1C3#1 1 0 … R1C3#2 0 1 … … … … … R2C1#1 1 0 … R2C1#2 0 1 … … … … … R2C2#1 1 0 … R2C2#2 0 1 … … … … … R2C3#1 1 0 … R2C3#2 0 1 … … … … … R3C1#1 1 0 … R3C1#2 0 1 … … … … … R3C2#1 1 0 … R3C2#2 0 1 … … … … … R3C3#1 1 0 … R3C3#2 0 1 … … … … …

La matrice 729×324 complète est disponible sur le site de Bob Hanson (en anglais).

Notez que l'ensemble des possibilités RxCy#z peut être arrangé comme un cube 9×9×9 dans un espace à 3 dimensions de coordonnes x, y et z. Ainsi, chaque ligne Rx, colonne Cy, ou nombre #z est une « tranche » 9×9×1 de possibilités. Chaque boîte Bw est un « tube » 9x3×3 de possibilités. Chaque ensemble de contraintes ligne-colonne RxCy, ensemble de contraintes ligne-nombre Rx#z, ou ensemble de contraintes colonne-nombre Cy#z est une « bande » 9x1×1 de possibilités. Chaque ensemble de contraintes boîte-nombre Bw#z est un « carré » 3x3×1 de possibilités. Et chaque possibilité RxCy#z est un « mini-cube » 1x1×1 consistant en une unique possibilité.

De plus, chaque ensemble de contraintes ou possibilité est l'intersection des ensembles de composants. Par exemple, R1C2#3 = R1 · C2 · #3, où "·" désigne l'ensemble d'intersection.

Bien que d'autres variations de Sudoku ont des nombres différents de lignes, colonnes, nombres et/ou différentes sortes de contraintes, ils impliquent tous des possibilités et des ensembles de contraintes, et ainsi peuvent être vus comme des problèmes d'ensembles intersectants exacts.

Généralisations

Rechercher des solutions

- Introduction - Énoncé - Généralisations - Représentation matricielle - Exemples plus approfondis - Rechercher des solutions - Preuve de la NP-complétude