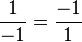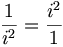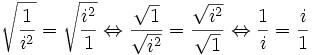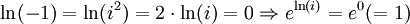Pseudo-démonstration d'égalité entre nombres - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le terme Pseudo-démonstration d'égalité renvoie à l'apparente exactitude de démonstrations d'égalités qui à l'évidence sont fausses. Étant donné que toute proposition fausse est équivalente à une autre proposition fausse, n'importe quel résultat faux est équivalent à
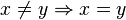
Nous nous contenterons ici de regarder le cas d'égalités entre nombres, et nous détaillerons différents vices parmi les plus répandus qui conduisent à ces erreurs. Les méthodes proposées dans cet article se veulent en outre les méthodes les plus courantes, les plus instructives, et dans la mesure du possible, les plus directes.
Pseudo-démonstration via des identités remarquables et division par zéro
Principe
Cette pseudo-démonstration s'appuie sur l'erreur suivante :
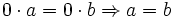
Elle s'effectue généralement en deux étapes :
- former via une identité remarquable un produit dans les deux membres d'une égalité dont l'un des facteurs est nul ;
- via une division par zéro obtenir un résultat absurde.
À noter que suivant l'identité remarquable utilisée et la manière dont on s'y prend, on peut obtenir n'importe quelle égalité fausse.
Le jeu consiste surtout à dissimuler la division par zéro dans des opérations très compliquées impliquant un grand nombre d'inconnues, ce qui rend difficile l'identification de la ligne fausse de la démonstration.
Cette technique est notamment utilisée pour « démontrer » que 1 + 1 = 3 dans L'Encyclopédie du savoir relatif et absolu de Bernard Werber.
Exemple
Étape 1:
- Soit a et b deux réels non nuls, on pose
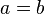
- On multiplie chaque membre par a
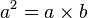
- On soustrait b2
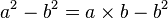
- On factorise chaque membre ( dans le premier on utilise une identité remarquable)
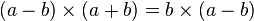
Étape 2:
- On divise par (a − b)
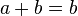
- Comme a = b, on remplace a par b
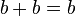
- Soit
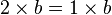
- On divise par b
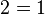
L'erreur est commise au moment ou l'on effectue la division par (a − b), car comme a = b alors a − b = 0 donc on divise par 0 ce qui est impossible.
- On commence avec la proposition suivante :
2 = 1 + 1 - On multiplie chaque membre par (2 − 1) :
2(2 − 1) = (1 + 1)(2 − 1) - On développe :
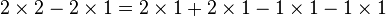
- On soustrait
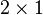
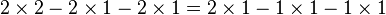
- On factorise :
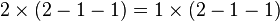
- On peut simplifier et on obtient :
2 = 1 - Il suffit d'ajouter 1 pour finalement avoir :
3 = 1 + 1
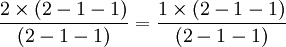
Pseudo-démonstration via des racines carrées non définies
Principe
Il s'agit ici de l'erreur courante
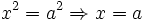
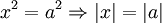
Deux étapes :
- écrire une égalité vraie entre carrés ;
- appliquer l'implication fausse en écrivant l'égalité sans les carrés (en invoquant une fonction racine non définie, par exemple dans
On peut généraliser ce principe aux exponentielles complexes en invoquant une fonction logarithme non définie dans l'ensemble de travail, par exemple
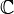
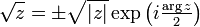
Exemples
Étape 1 :
Considérons l'égalité − 1 = − 1, qui peut s'écrire sous forme de quotients :
Or − 1 = i2 (voir nombre imaginaire), d'où
Étape 2 :
On prend la racine carrée des deux côtés ce qui donne :
En multipliant par i de part et d'autre, on obtient
- 1 = i2
Et puisque i2 = − 1, nous avons alors
- 1 = − 1
- ln( − 1) + ln( − 1) = ln(( − 1)2) = ln(1) = 0
Ainsi,
Et comme l'exponentielle est l'application réciproque du logarithme népérien :
- i = 1