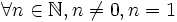Pseudo-démonstration d'égalité entre nombres - Définition
La liste des auteurs de cet article est disponible ici.
Pseudo-démonstration via des équations et confusion condition nécessaire et suffisante
Principe
Une autre pseudo-démonstration courante est de restreindre l'ensemble des solutions possibles d'une équation puis d'affirmer qu'un des éléments de l'ensemble est racine. Cela revient à faire l'erreur de logique suivante :
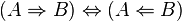
Elle se déroule ainsi :
- étude de l'équation (restriction de l'ensemble des solutions possibles à un faible nombre, une ou deux) ;
- affirmation de l'ensemble des solutions possibles comme ensemble des solutions ;
- test de l'une des supposés racines et résultat absurde.
Exemple
Étape 1 :
Considérons l'équation :
- x2 + x + 1 = 0
Ses solutions sont également celles (à l'exception de zéro) de :
Or d'après l'équation initiale :
Donc :
- x3 = − ( − x − 1) − x = 1
Étape 2 : La seule racine réelle possible est 1.
Étape 3 : En remplaçant x par 1 dans l'équation initiale, on obtient l'égalité 3 = 0.
Pseudo-démonstration via un changement de variable non licite lors d'une intégration
Principe
Lorsque l'on effectue un changement de variable lors d'une intégration sur un segment, il faut que le changement de variable soit un C1-difféomorphisme. Si le changement de variable est effectué trop hâtivement, il n'est pas rare de trouver un résultat absurde en fin d'intégration.
Démarche :
- calculer l'intégrale de manière correcte ;
- effectuer un changement de variable erroné ;
- confronter les deux résultats.
Exemple
Étape 1 :
Considérons l'intégrale :
Par intégration en tant que monôme du second degré :
Étape 2 :
Effectuons le changement de variable de classe
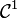
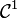
Ainsi :
D'où :
Étape 3 :
Des deux calculs de l'intégrale on en déduit :
Pseudo-démonstration via une sommation floue
Principe
En écrivant une somme de manière floue, c’est-à-dire non pas de manière formelle :
mais avec des points de suspensions :
la variable muette de sommation (notée ici k) est véritablement passée sous silence et le manque de formalisme des points de suspensions sert à masquer l'erreur.
Méthodologie :
- faire des calculs sur une somme ;
- générer une erreur via l'ensemble de définition de la variable muette, autrement dit le nombre de termes ;
- aboutissement à un résultat absurde.
Variantes
La dérivation va s'effectuer différemment suivant le membre de l'égalité, à gauche il sera question d'une dérivation correcte, et à droite une dérivation sans tenir compte que la variable x est aussi le cardinal de l'ensemble des termes.
Étape 1 : Soit x un entier. Par définition de la fonction carrée :
-

Étape 2 : En dérivant par rapport à x :
-
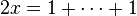
Étape 3 : d'où en simplifiant par x :
- 2 = 1
Cette variante joue sur le nombre de termes de la somme des termes d'une suite arithmétique (ici la suite des n premiers entiers).
Étape 1 :
La somme des termes des n premiers entiers s'écrit :
Cela est vrai également au rang n − 1 :
D'où en ajoutant 1 dans chacun des membres :
Étape 2 :
Cette égalité peut aussi s'écrire :
D'après l'égalité au rang n, on a donc :
D'où :
Étape 3 :
Finalement :
L'erreur vient du fait que l'on compare les sommes
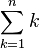
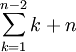
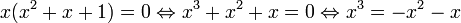
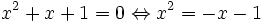
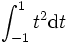
![\int_{-1}^1 t^2 {\rm d}t=\left[\frac{t^3}{3}\right]_{-1}^{1}=\frac{2}{3}](https://static.techno-science.net/illustration/Definitions/autres/5/5550a80b7f059e0d0e21a231a0427120_b7d08092edec3c99e95d47ca0a890487.png)
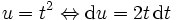
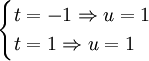
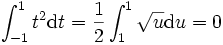
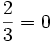
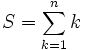
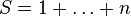
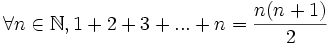
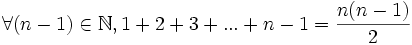
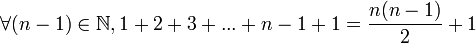
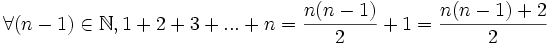
![\forall (n - 1) \in \mathbb{N}, \left[ \frac{n(n+1)}{2} = \frac{n(n-1) + 2}{2} \Leftrightarrow n(n+1) = n(n-1) + 2 \right]](https://static.techno-science.net/illustration/Definitions/autres/f/f5176c9c07faee57c7b04c5d09a2a67e_1f93512249fe94b8eb881ddbe3c95a84.png)
![\forall (n - 1) \in \mathbb{N}, \left[ n^2 + n = n^2 - n + 2 \Leftrightarrow 2n = 2 \right]](https://static.techno-science.net/illustration/Definitions/autres/6/6a7da32ae9632342b85cf2e2e61ae932_4797b26b23535b4da5f930a6b62a49e6.png)