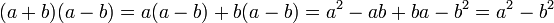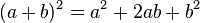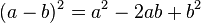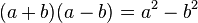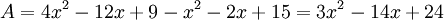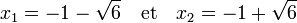Identité remarquable - Définition

Introduction

En mathématiques, on appelle identités remarquables ou encore égalités remarquables certaines égalités qui s'appliquent à des nombres. Elles servent en général à accélérer les calculs, à simplifier certaines écritures, à factoriser ou à développer des expressions. Elles servent pour la résolution des équations du second degré et sont plus généralement utiles pour la recherche de solutions d'équations.

La plupart de ces identités remarquables ont tout d'abord été démontrées à l'aide de raisonnements géométriques puis ont été généralisées à des puissances supérieures par des calculs algébriques.

Identités remarquables du second degré

Énoncés

Les trois identités remarquables du second degré sont :

La deuxième de ces identités peut être vue comme un cas particulier de la première, en prenant, au lieu de b, -b dans la première égalité. Ces égalités font l'objet d'un vocabulaire spécifique :

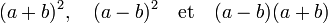
On définit de même :

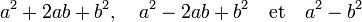
Ici a et b désignent des nombres, qui peuvent être des entiers, des rationnels et réels, ou même des complexes. Ces identités sont vraies dans un cadre général, elles sont aussi valables dans un anneau, à condition que a et b commutent.

Exemples

Développement et réduction

Les identités remarquables permettent de transformer l'écriture de certaines expressions algébriques, comme dans l'exemple suivant :

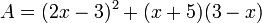
L'expression A est la somme de deux termes. Le premier terme est un produit remarquable, que l'on peut transformer en somme :

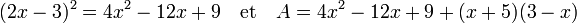
Le deuxième terme se traite à l'aide de la distributivité de la multiplication par rapport à l'addition :

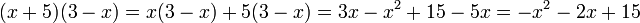
En additionnant termes à termes, on obtient :

Équation du second degré

Les identités remarquables permettent de résoudre une équation du second degré. Illustrons la méthode sur l'exemple suivant :

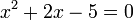
La méthode consiste à travailler la partie de l'expression qui ne dépend pas de x de manière à utiliser une des deux premières identités remarquables et factoriser la partie qui dépend de x :

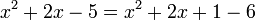
Les trois premiers termes sont maintenant une somme remarquable, il est possible d'appliquer une identité remarquable et l'équation devient :

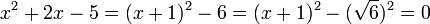
On reconnaît une nouvelle somme remarquable, l'équation s'écrit encore :

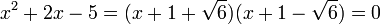
Un produit a.b de deux nombres a et b est nul si, et seulement si, a ou b est nul. Résoudre l'équation revient à résoudre deux équations du premier degré :

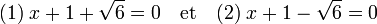
On trouve les deux racines :

Identité remarquable et géométrie

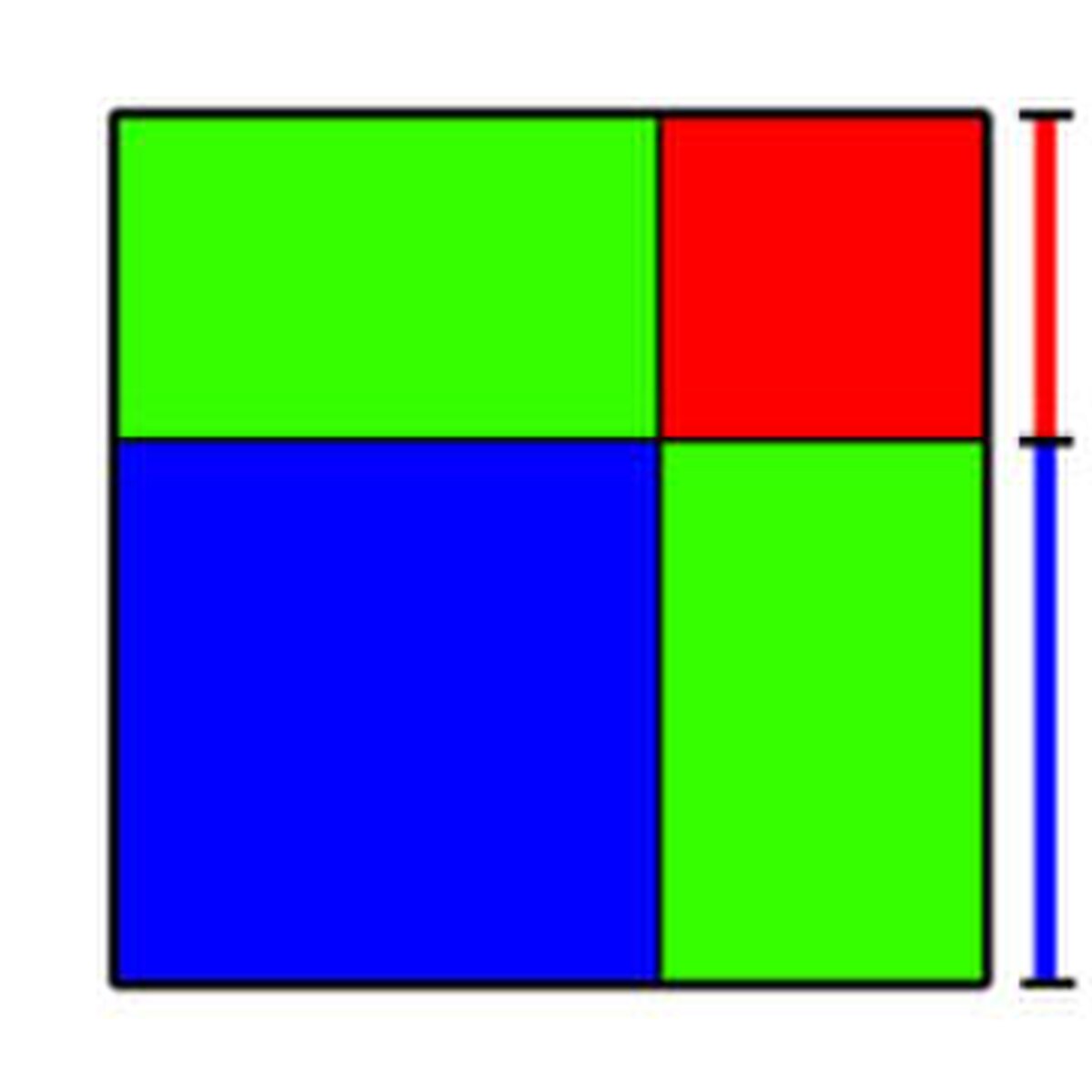
Ces identités remarquables sont connues depuis les babyloniens. Il est possible qu'ils se soient rendu compte de ces égalités à l'aide de raisonnements géométriques. Il existe une méthode simple pour trouver la formule suivante:

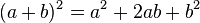
Pour se convaincre de la véracité de la formule, on considère la figure de droite. Elle représente un carré. On suppose que la longueur côté du carré bleu est égale à a et celle du carré rouge à b. L'aire du grand carré est égale à (a + b)². Il existe une autre manière d'exprimer cette aire, elle est la somme des aires bleue, rouge et des deux zones vertes. L'aire bleue est égale à a² car c'est un carré de côté a, l'aire rouge est égale à b² et chaque rectangle vert possède des côtés de longueur a et b, leur aire est égale à a.b. Comme il existe deux rectangles verts, on obtient bien la formule annoncée.

Démonstration par l'algèbre

L'algèbre permet encore de démontrer ces formules. Calculons (a - b)². La distributivité montre que :

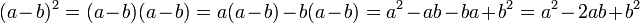
On démontre de même la troisième identité remarquable :