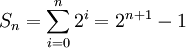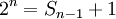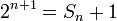Puissance de deux - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Autres puissances de deux remarquables
- 224 = 16 777 216, le nombre de couleurs uniques qui peuvent être affichées en couleurs vraies, qui est utilisée par la plupart des écrans d'ordinateur.
Ce nombre est le résultat de l'utilisation du système à trois canaux RVB, avec 8 bits pour chaque canal, ou 24 bits au total.
Puissances de deux qui ont comme exposant des puissances de deux
Les cellules de mémoires modernes et les registres manipulent souvent un nombre de bits qui est une puissance de deux, les puissances les plus fréquentes qui apparaissent sont celles dont l'exposant est aussi une puissance de deux.
Une courte liste de certaines d'entre-elles :
| 2 | = | 21 |
| 4 | = | 22 |
| 16 | = | 24 |
| 256 | = | 28 |
| 65 536 | = | 216 |
| 4 294 967 296 | = | 232 |
| 18 446 744 073 709 551 616 | = | 264 |
| 340 282 366 920 938 463 463 374 607 431 768 211 456 | = | 2128 |
| 115 792 089 237 316 195 423 570 985 008 687 907 853 269 984 665 640 564 039 457 584 007 913 129 639 936 | = | 2256 |
Théorèmes
- La somme des puissances de 2 est égale à la puissance de deux suivante moins un.
- Une puissance de deux est égale à la somme de toutes les puissances de deux inférieures plus un.
- Un entier est divisible par
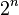
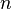
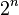
- Les puissances de 2 sont les seuls nombres qui ne sont pas divisibles par un nombre impair autre que 1.
- Une puissance de 2 peut s'écrire sous la forme
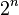
- Tout autre nombre s'écrit en produit de facteur premier 2^n*k^l, k étant un nombre premier supérieur à 2 et l un entier naturel supérieur ou égal à 1, or tout nombre premier supérieur à 2 est un nombre impair.