Puissance de deux - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, une puissance de deux est n'importe quel entier positif mis en exposant du nombre deux ; en d'autres mots, deux fois lui-même un certain nombre de fois. Un est une puissance (la puissance zéro) de deux. Écrite en binaire, une puissance de deux est toujours de la forme 10000…0, comme une puissance de dix dans le système décimal.
Comme deux est la base du système binaire, les puissances de deux sont importantes en informatique. De manière plus précise, deux à la puissance n est le nombre de façons dont les bits dans un entier binaire de longueur n peuvent être arrangés, et ainsi ces nombres représentent une puissance de deux moins un dénotent la limite supérieure des entiers s'ils sont interprétés en tant qu'entiers sans signe (représenter la puissance de 2 elle-même (sans le -1) demanderait un bit de plus).
Les nombres de cette forme apparaissent parfois dans les logiciels. Par exemple, dans le jeu vidéo The Legend of Zelda pour la console de jeu Nintendo 8 bits, on peut seulement travailler avec des nombres longs de 8 bits - le contenu d'un octet, utilisé pour stocker un nombre, donné par une valeur maximale de 2-1 = 255.
Les tailles de mémoire des ordinateurs utilisent aussi les puissances de 2. Un octet contient (2) bits, et un kilooctet contient 1 024 (2) octets. Presque tous les registres de processeurs ont des tailles qui sont des puissances de deux (on est actuellement en train d'entamer une transition de 32 à 64 sur les PC).
Les puissances de deux ont occupé une place dans les anciens lecteurs de disques : taille de secteur, nombre de secteur par piste, et/ou nombre de piste par surface étaient souvent des puissances de deux. Les disques avaient alors ce que l'on nommait une géométrie (nombre fixe de secteurs par piste), ce qui a fini par être abandonné au profit d'une densité d'enregistrement à peu près constante (davantage de secteurs vers l'extérieur) au prix d'un peu d'électronique additionnelle.
La taille du bloc logique est restée, pour des raisons historiques et de commodité de calcul, une puissance de deux.
On retrouve dans les résolutions vidéo des nombres qui ne sont pas des puissances de deux, mais sont souvent la somme ou le produit de deux ou trois puissances de deux, ou des puissances de deux moins un. Par exemple, 640 = 512 + 128, et 480 = 32 × 15, une résolution adaptée aux écrans de diagonale 14′′.
On nomme nombre premier de Mersenne un nombre premier de la forme
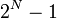
On peut aussi remarquer que le chiffre de l'unité est une suite (2,4,8,6) : 21 = 2, 22 = 4, 23 = 8, 24 = 16, 25 = 32, 26 = 64, ...
Les quarante premières puissances de deux
| | | 2 | | | 2 048 | | | 2 097 152 | | | 2 147 483 648 | |||
| | | 4 | | | 4 096 | | | 4 194 304 | | | 4 294 967 296 | |||
| | | 8 | | | 8 192 | | | 8 388 608 | | | 8 589 934 592 | |||
| | | 16 | | | 16 384 | | | 16 777 216 | | | 17 179 869 184 | |||
| | | 32 | | | 32 768 | | | 33 554 432 | | | 34 359 738 368 | |||
| | | 64 | | | 65 536 | | | 67 108 864 | | | 68 719 476 736 | |||
| | | 128 | | | 131 072 | | | 134 217 728 | | | 137 438 953 472 | |||
| | | 256 | | | 262 144 | | | 268 435 456 | | | 274 877 906 944 | |||
| | | 512 | | | 524 288 | | | 536 870 912 | | | 549 755 813 888 | |||
| | | 1 024 | | | 1 048 576 | | | 1 073 741 824 | | | 1 099 511 627 776 |

















































