Séparation des convexes - Définition
La liste des auteurs de cet article est disponible ici.
Théorèmes de séparation au sens large
Deux jeux d'hypothèses permettent d'assurer la séparation au sens large. Le premier des théorèmes qui suit est parfois appelé « première forme géométrique du théorème de Hahn-Banach ».
Théorème — Soit E un espace normé, A et B deux convexes de E non vides et disjoints. On suppose A ouvert. Alors il existe un hyperplan fermé séparant A et B.
Théorème — Soit E un espace affine de dimension finie, A et B deux convexes de E non vides et disjoints. Alors il existe un hyperplan séparant A et B.
En revanche, en dimension infinie, on ne peut pas toujours construire un hyperplan fermé de séparation large : il existe un exemple de deux convexes fermés non vides et disjoints mais qui ne peuvent être séparés par un hyperplan fermé.
On pourra remarquer que, dans le premier théorème, le convexe ouvert est nécessairement inclus dans un demi-espace strict. En particulier lorsque A et B sont tous les deux ouverts, on a réalisé une séparation où chacun des convexes est inclus dans un des demi-espaces stricts : c'est mieux qu'une séparation large, mais moins bien qu'une séparation stricte au sens qui a été choisi dans cet article.
Principe de la démonstration
Le premier théorème ci-dessus découle assez rapidement de la version de la « forme géométrique du théorème de Hahn-Banach » donnée dans l'article Théorème de Hahn-Banach. L'idée supplémentaire nécessaire pour conclure est de considérer l'ensemble A − B c'est-à-dire l'ensemble des a − b, où a varie dans A et b dans B. On vérifie sans mal que c'est un convexe ouvert C. On peut alors appliquer le théorème mentionné à l'article Théorème de Hahn-Banach à ce convexe C et à L = {0}, qui fournit un hyperplan H1 ; il est alors facile de constater que parmi les hyperplans parallèles à H1 l'un répond à la question.
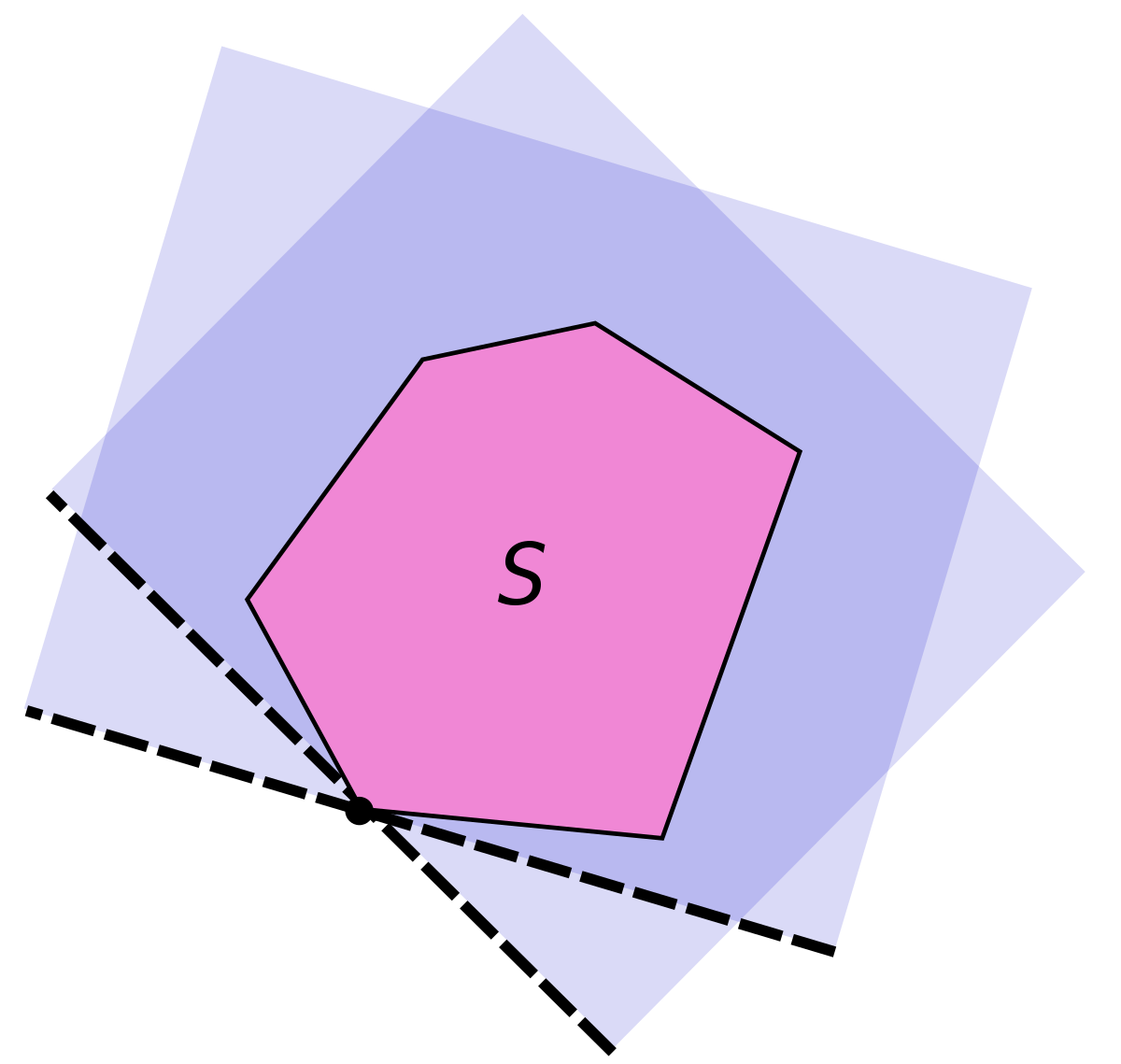
Hyperplans d'appui
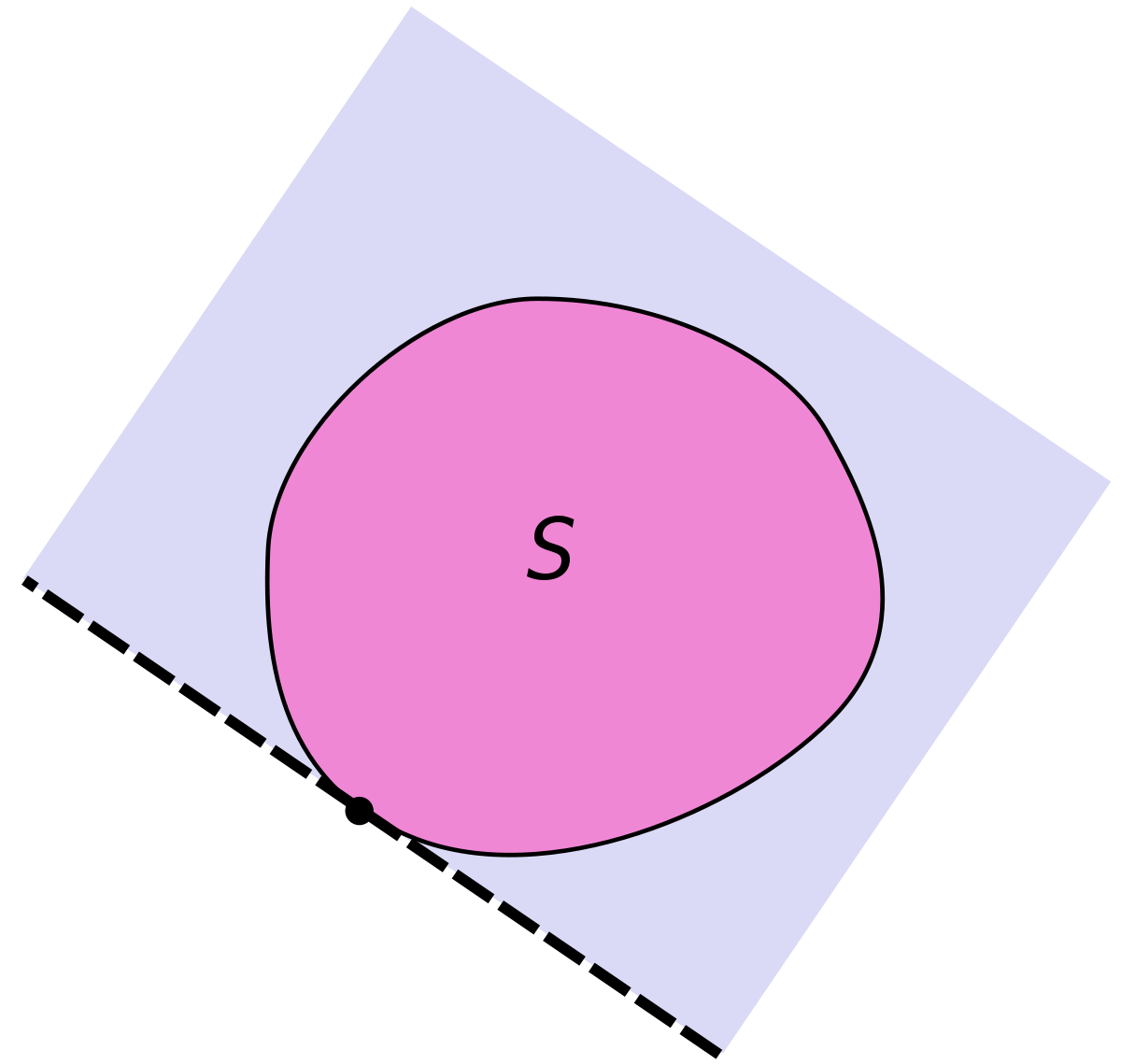
Un cas particulièrement important est celui où B est un singleton contenant un seul point x0, choisi sur la frontière de A.
Commençons par une définition : pour A partie d'un espace vectoriel sur

On peut alors énoncer :
Théorème — Dans un espace affine de dimension finie, soit C un convexe fermé et x0 un point de la frontière de C. Il existe au moins un hyperplan d'appui de C en x0.
Pour le prouver, on se débarrasse d'abord du cas dégénéré où la dimension de C serait plus petite que celle de l'espace ambiant : si c'est ainsi, n'importe quel hyperplan affine contenant l'enveloppe affine de C convient. Une fois ce cas éliminé, l'intérieur int(C) n'est pas vide et on peut appliquer le théorème de séparation à l'ouvert int(C) et au singleton {x0}, qu'on sépare par un hyperplan H. Comme C est l'adhérence de son intérieur (voir l'article Adhérence, intérieur et frontière d'un convexe), il est lui aussi inclus dans un des demi-espaces délimités par H, et cet hyperplan répond donc au cahier des charges.
Les hyperplans d'appui sont des outils fondamentaux pour classifier les points au bord d'un polyèdre convexe en sommets, points des arêtes, points des faces, etc... et plus généralement pour distinguer et étudier des points et parties remarquables de la frontière d'un convexe.