Séparation des convexes - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Étant donnés deux convexes d'un même plan ne se rencontrant pas, il est toujours possible de subdiviser le plan en deux demi-plans de sorte que chacun contienne entièrement l'un des convexes. Il en est de même en dimension 3, la séparation des convexes étant alors réalisée par un plan. Plus généralement, on peut en faire autant en dimension finie quelconque à l'aide d'un hyperplan. Sous une hypothèse convenable de compacité on peut même garantir une « séparation stricte », assurant que chacun des deux convexes reste à distance de l'hyperplan qui les sépare ; dans de bonnes conditions la séparation peut également être assurée dans certains espaces vectoriels topologiques de dimension infinie.
Un cas particulier remarquable est celui où l'un des convexes ne contient qu'un point, choisi sur la frontière de l'autre. Dans ce cas, les hyperplans séparants sont appelés hyperplans d'appui du convexe.
Position du problème
On se place dans un espace affine E (de dimension finie), ou dans un espace vectoriel normé sur

Étant donné un hyperplan affine H de E, il existe une forme linéaire (unique à un facteur multiplicatif près) qui puisse servir d'équation à H, c'est-à-dire pour laquelle il existe un c réel tel que
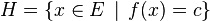
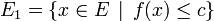
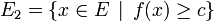
Étant données deux parties A et B de E, on dit alors que H sépare A et B lorsque, dans la subdivision de E par H en deux demi-espaces E1 et E2, l'un des ensembles A et B est inclus dans E1 et l'autre dans E2. Dans cette définition (séparation au sens « large »), on n'interdit pas à A et à B de contenir des points de H, voire de se rencontrer l'un l'autre à condition que ce soit sur H.
Sous certaines hypothèses, on peut obtenir des résultats de séparation plus précis et conclure que A et B sont de part et d'autre de H, dans les demi-plans stricts qu'il limite. De fait, on peut parfois faire encore un peu mieux, d'où la définition technique suivante : on dit que H d'équation
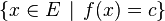
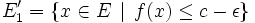
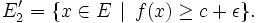
Théorème de séparation stricte
Ce résultat est la « deuxième forme géométrique du théorème de Hahn-Banach » :
Théorème — Soit E un espace normé, A et B deux convexes de E non vides et disjoints. On suppose A fermé et B compact. Alors il existe un hyperplan fermé séparant strictement A et B.
Une application particulièrement importante en est la représentation des convexes fermés comme intersection de demi-espaces fermés. Lorsqu'on intersecte des demi-espaces fermés, le résultat de l'opération est de façon évidente un convexe fermé (puisque tant la convexité que la fermeture sont conservées par intersection, même infinie). Il se trouve que la réciproque est vraie :
Corollaire — Dans un espace normé E, tout convexe fermé est l'intersection des demi-espaces fermés qui le contiennent.
Principes des démonstrations
Pour le théorème, on remarque dans un premier temps que la distance d qui sépare A et B est strictement positive (c'est toujours le cas pour la distance entre un fermé et un compact dans un espace métrique). On pose ε = d / 3 et on considère A' (resp. B'), ensembles des points à distance ε de A (resp. B), qui sont encore convexes mais sont eux des ouverts, tout en restant disjoints. On applique à ces ouverts le théorème de séparation au sens large, et on vérifie enfin sans mal que l'hyperplan obtenu sépare de fait strictement A de B.
Pour le corollaire, on prend x0 un point quelconque du complémentaire du convexe fermé C. En appliquant le théorème à C et {x0} on obtient un demi-espace fermé contenant C mais auquel x0 n'appartient pas, ce qui prouve que x0 n'est pas dans l'intersection des demi-espaces fermés contenant C. L'inclusion non évidente est ainsi prouvée.
En dimension finie, on peut aussi démontrer cette forme du théorème de séparation en se reposant sur le théorème de projection sur un convexe fermé. En effet si A est fermé et B est un singleton (contenant un point x0 extérieur à A), on peut trouver un hyperplan les séparant en projetant x0 sur A en un point
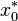
![[x_0,x_0^*]](https://static.techno-science.net/illustration/Definitions/autres/4/4878a1f781145a4d9dafef3bd92a5b9b_0db77f21555f7aec975523f3e2bed765.png)


















































