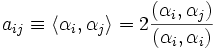Système de racines - Définition
La liste des auteurs de cet article est disponible ici.
Matrice de Cartan
Étant donné le système de racines simples
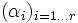
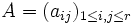
L'intérêt de la matrice de Cartan est que sa seule donnée est suffisante pour reconstruire l'ensemble de tout le système de racines. C'est donc une façon théorique et pratique très utile de coder l'ensemble de l'information contenue dans un système de racines. Pour représenter graphiquement la matrice de Cartan on utilise le concept de diagramme de Dynkin qu'on va maintenant aborder.
Systèmes de racines et théorie de Lie
Les systèmes de racines classent un nombre d'objets reliés dans la théorie de Lie, notamment :
- Les algèbres de Lie simples complexes
- Les groupes de Lie simples complexes
- Les groupes de Lie complexes simplement connexes qui sont simples modulo leur centre
- Les groupes de Lie compacts simples
Dans chaque cas, les racines sont les poids différents de zéro de la représentation adjointe.
Liste des systèmes de racines irréductibles
La table suivante liste certaines propriétés des systèmes de racines irréductibles. Les constructions explicites de ces systèmes sont données dans les parties suivantes.
|
|
|
| I |
|
|---|---|---|---|---|
| An | n(n+1) | n+1 | (n+1)! | |
| Bn | 2n2 | 2n | 2 | 2n n! |
| Cn | 2n2 | 2n(n−1) | 2 | 2n n! |
| Dn | 2n(n−1) | 4 | 2n−1 n! | |
| E6 | 72 | 3 | 51 840 | |
| E7 | 126 | 2 | 2 903 040 | |
| E8 | 240 | 1 | 696 729 600 | |
| F4 | 48 | 24 | 1 | 1 152 |
| G2 | 12 | 6 | 1 | 12 |
Ici
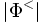
An
Soit V, le sous-espace de
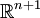

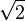
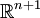
Bn
Soit
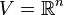

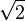
Cn
Soit
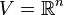

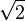
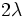

Dn
Soit
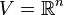

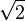
E6, E7, E8
Soit
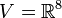

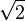
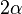
En ce qui concerne E7, il peut être construit comme l'intersection de E8 avec l'hyperplan de vecteurs perpendiculaires à une racine fixée

Finalement, E6 peut être construit comme l'intersection de E8 avec deux tels hyperplans, correspondant aux racines

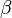
Les systèmes de racines E6, E7 et E8 ont respectivemet 72, 126 et 240 racines.
F4
Pour F4, soit
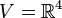


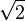
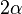
G2
Il existe 12 racines dans G2, qui forment les sommets d'un hexagramme. Voir l'image ci-dessus.