Système de racines - Définition

Classification

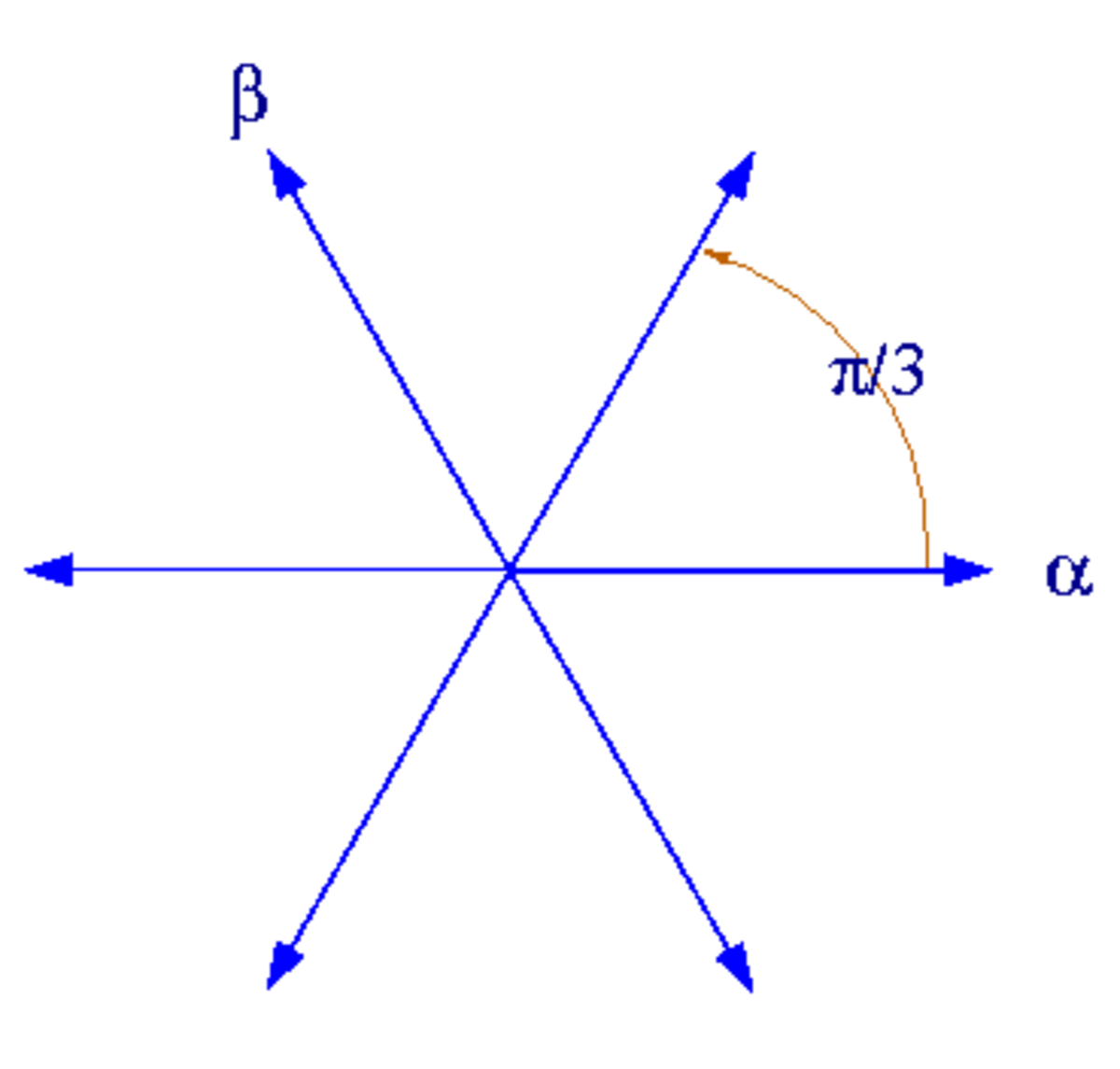
Il existe seulement un système de racines de rang 1 constitué de deux vecteurs différents de zéro . Ce système de racines est appelé . Dans le rang 2, il existe quatre possibilités :

Système de racines de rang 2

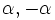
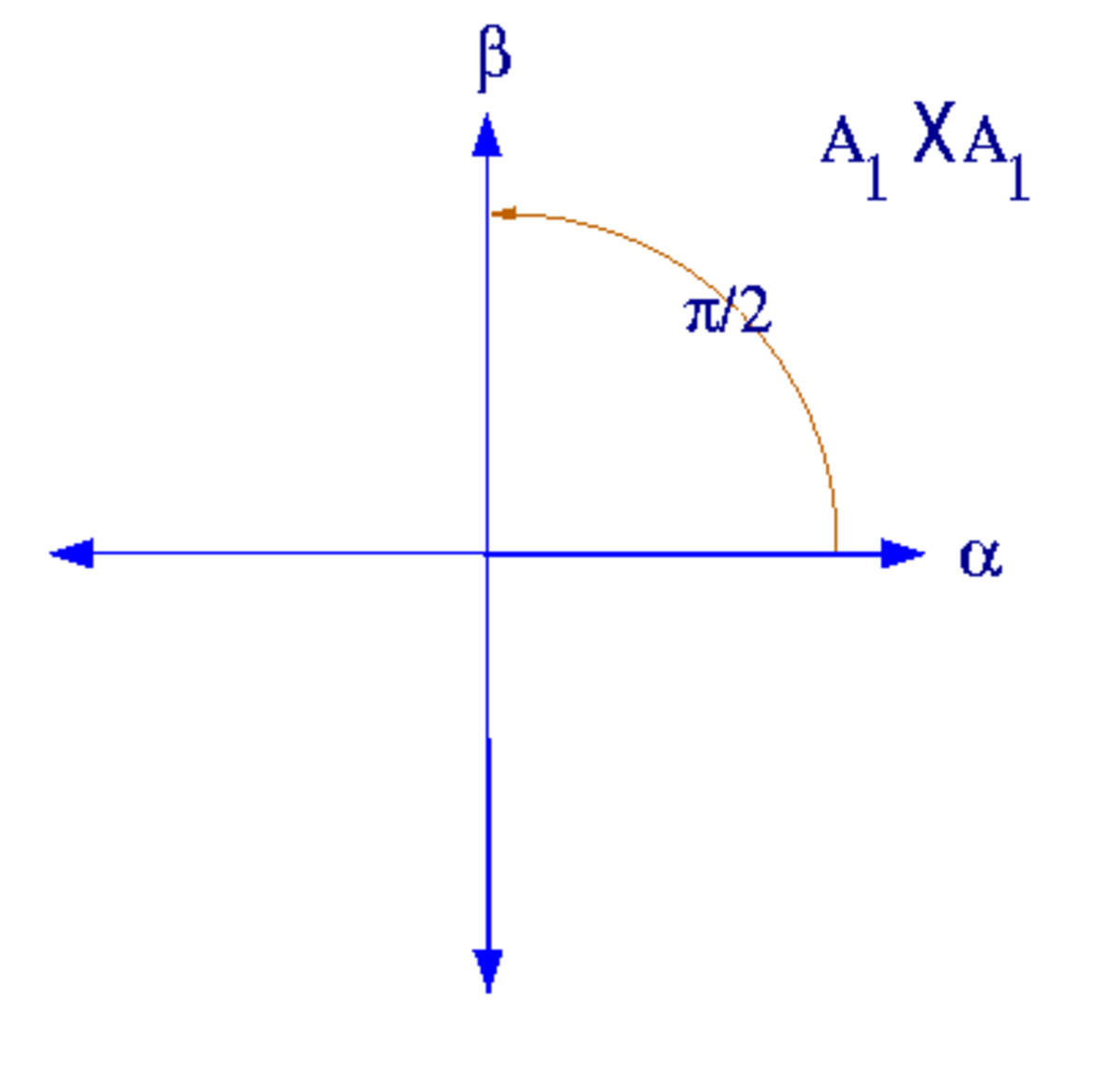
Système de racines A1×A1	Système de racines A2
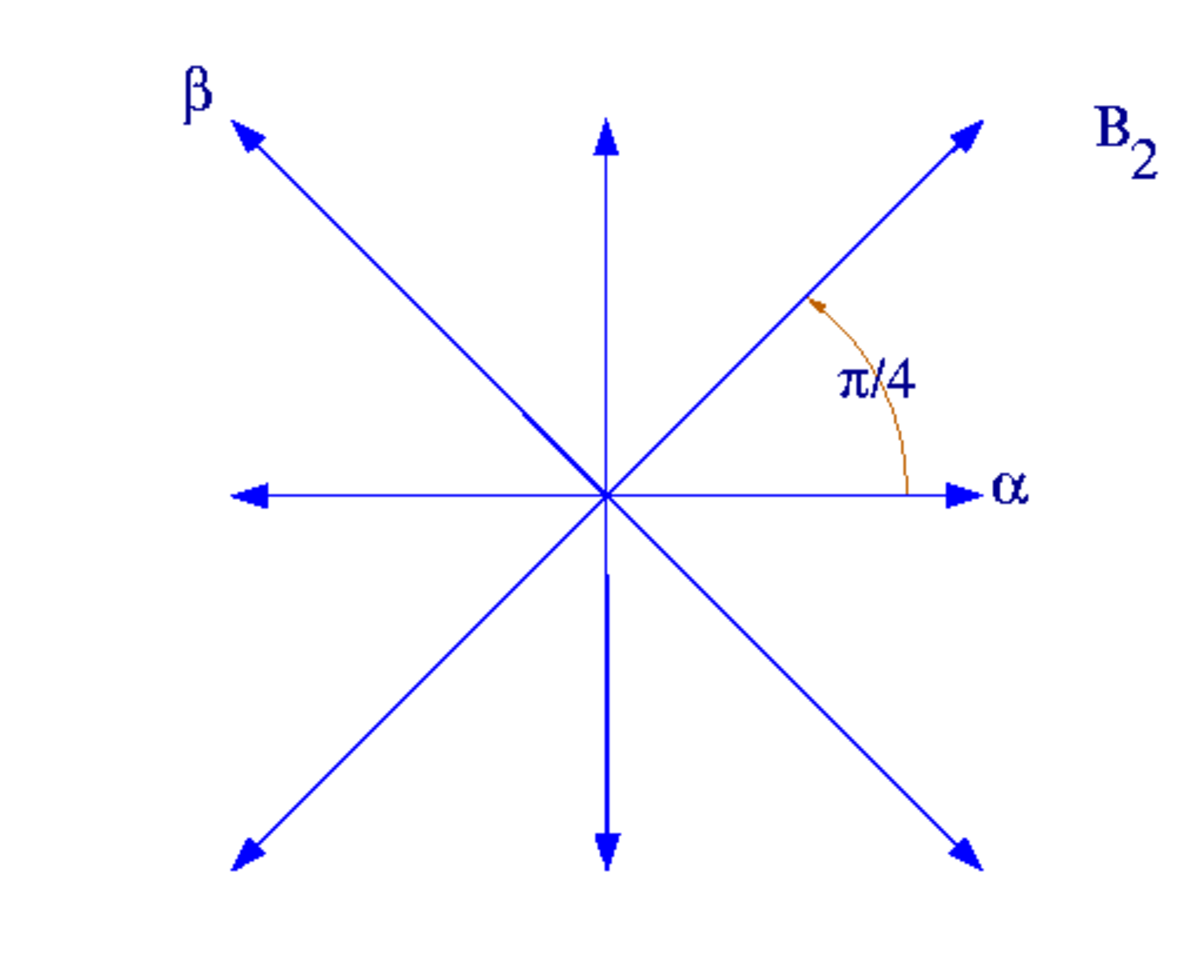
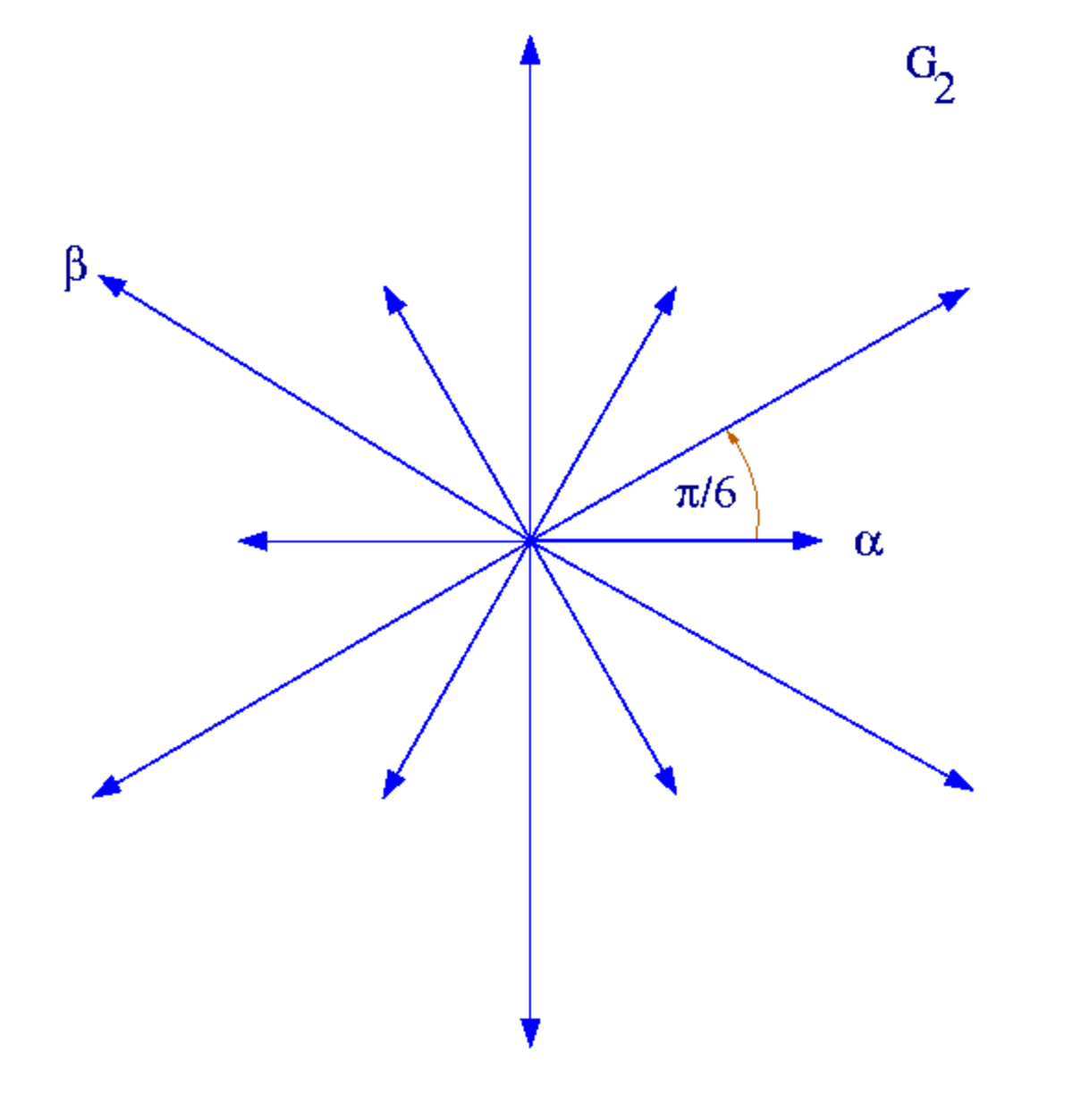
Système de racines B2	Système de racines G2

Si est un système de racines dans V et W est un sous-espace de V traversé par , alors est un système de racines dans W. Ainsi, notre liste exhaustive de système de racines de rang 2 montre les possibilités géométriques pour deux racines quelconques dans le système de racines. En particulier, deux racines de cette sorte se rencontrent à un angle de 0, 30, 45, 60, 90, 120, 135, 150 ou 180 degrés.

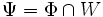
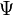
En général, les systèmes de racines irréductibles sont précisés par une famille (indiquée par une lettre de A à G) et le rang (indiqué par un indice). Il existe quatre famille infinies (appelées les systèmes de racines classiques) et cinq cas exceptionnels (les systèmes de racines exceptionnels) :

• 
• 
• 
• 
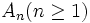
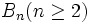
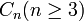
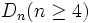
• E₆
• E₇
• E₈
• F₄
• G₂

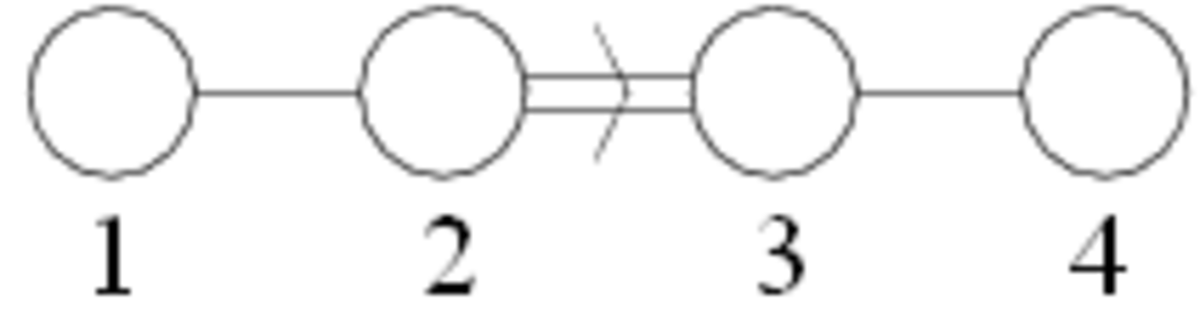
Diagrammes de Dynkin

Pour démontrer ce théorème de classification, on peut utiliser les angles entre les paires de racines pour encoder le système de racines dans un objet combinatoire plus simple, le diagramme de Dynkin, nommé en l'honneur de Eugene Dynkin. Les diagrammes de Dynkin peuvent alors être classés selon l'arrangement donné ci-dessus.

À chaque système de racines est associé un graphe (probablement avec un bord particulièrement marqué) appelé le diagramme de Dynkin lequel est unique à un isomorphisme près. Le diagramme de Dynkin peut être extrait du système de racines en choisissant un ensemble de racines simples.

Les sommets du diagramme de Dynkin correspondent aux vecteurs dans . Une arête est dessinée entre chaque paire de vecteurs non orthogonaux; il y a une seule arête non orientée s'ils font un angle de 120 degrés, une double arête orientée s'ils font un angle de 135 degrés et une triple arête orientée s'ils font un angle de 150 degrés (on démontre en effet que deux éléments distincts de forment toujours un angle obtus). En plus, les doubles et triples arêtes sont marquées avec un signe d'angle pointant vers le vecteur le plus court.

Bien qu'un système de racines donné possède plus d'une base, le groupe de Weyl agit transitivement sur l'ensemble des bases. Par conséquent, le système de racines détermine le diagramme de Dynkin. Étant donnés deux systèmes de racines avec le même diagramme de Dynkin, nous pouvons faire coïncider les racines, démarrant avec les racines dans la base, et montrer que les systèmes sont en fait les mêmes.

Ainsi, le problème de classification des systèmes de racines se réduit au problème de classification des diagrammes de Dynkin possibles, et le problème de classification des systèmes de racines irréductibles se réduit au problème de classification des diagrammes de Dynkin connectés. Les diagrammes de Dynkin encodent le produit intérieur sur E en termes de base , et la condition que ce produit interne doit être défini positif s'avère être tout ce qui est nécessaire pour obtenir la classification désirée. Les diagrammes connectés réels sont les suivants :

Diagramme	Nom du groupe
	An
	Bn
	Cn
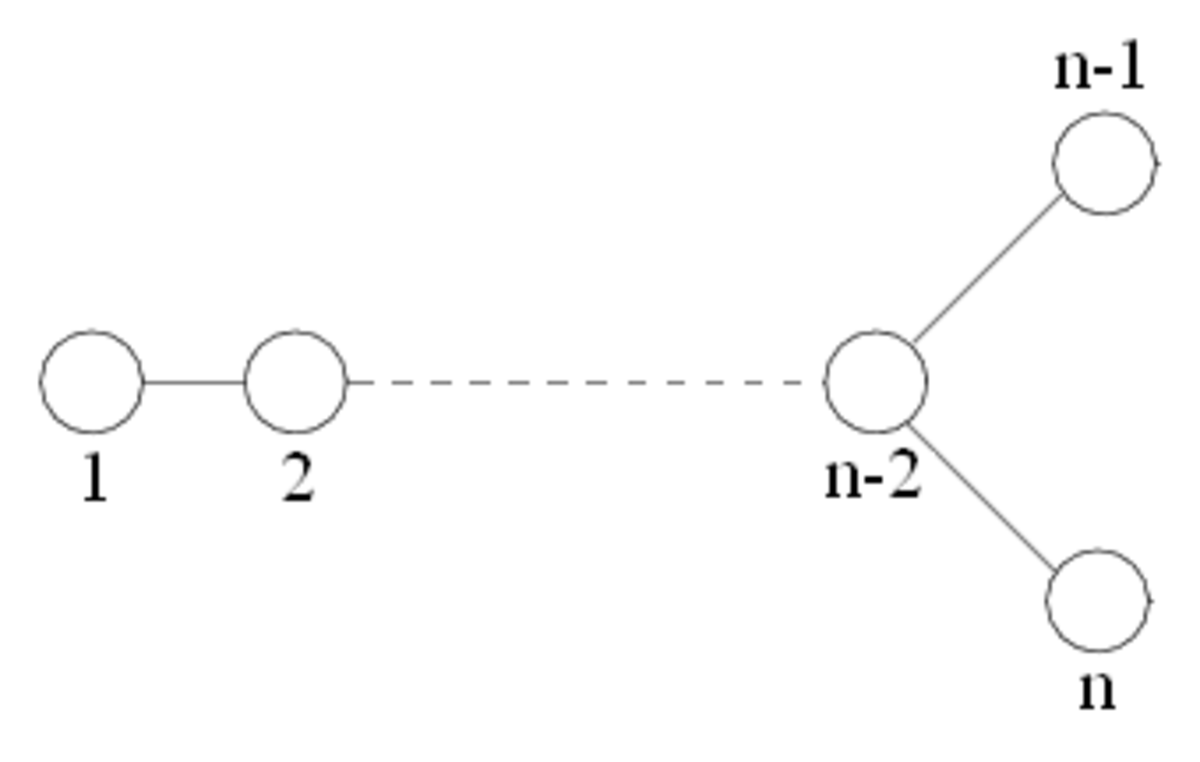
	Dn
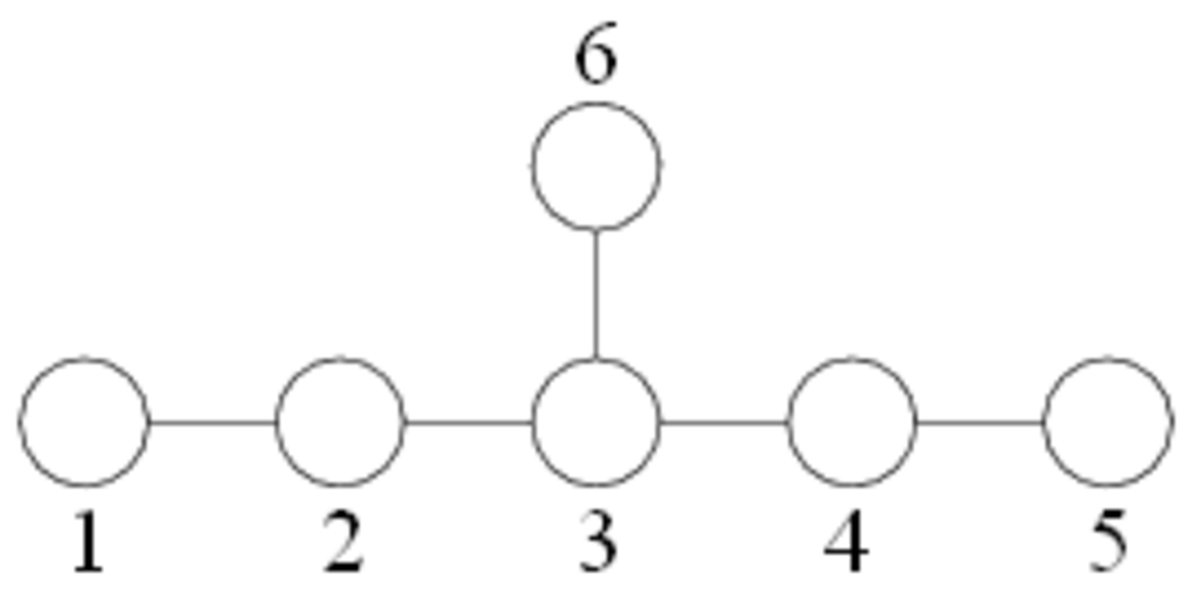
	E6
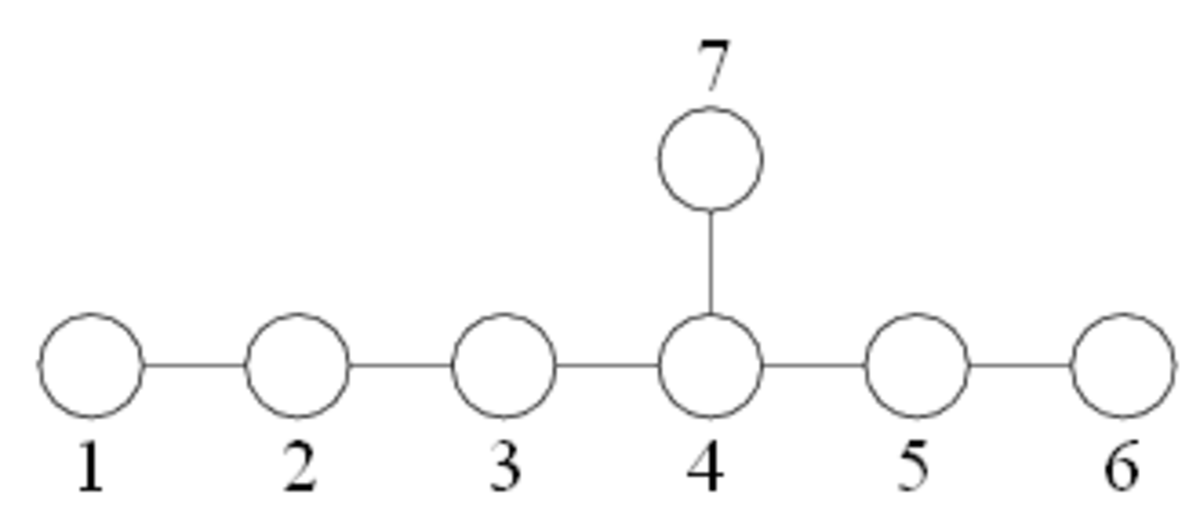
	E7
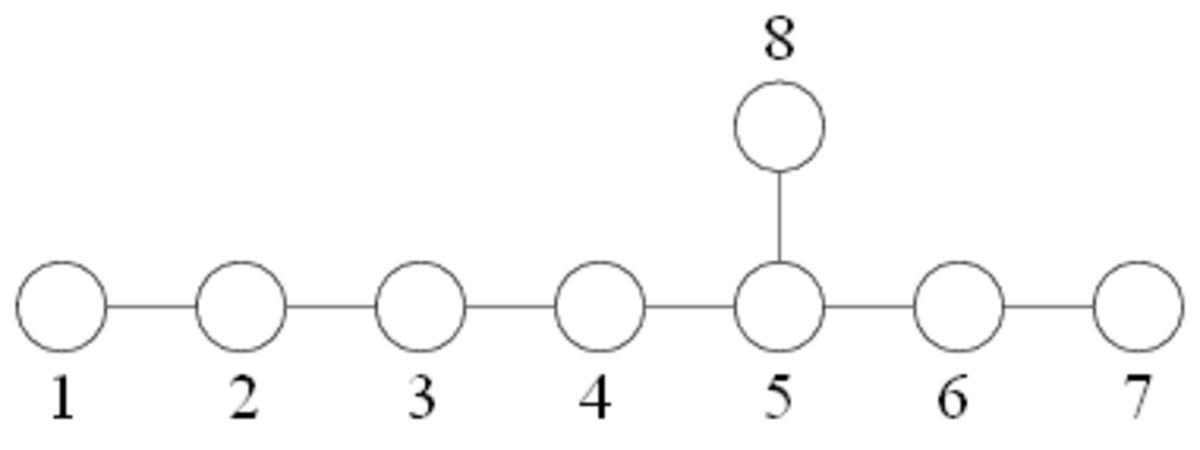
	E8
	F4
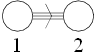
	G2