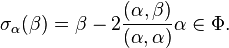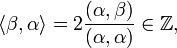Système de racines - Définition

Introduction

En mathématiques, un système de racines est une configuration de vecteurs dans un espace euclidien qui vérifie certaines conditions géométriques. Cette notion est très importante dans la théorie des groupes de Lie. Comme les groupes de Lie et les groupes algébriques sont maintenant utilisés dans la plupart des parties des mathématiques pendant le XX^e siècle, la nature apparemment spéciale des systèmes de racines est en contradiction avec le nombre d'endroits dans lesquels ils sont appliqués. Par ailleurs, le schéma de classification des systèmes de racines, par les diagrammes de Dynkin, apparait dans des parties des mathématiques sans aucune connexion manifeste avec les groupes de Lie (telle que la théorie des singularités).

Définitions

Soit V un espace euclidien de dimension finie, muni du produit scalaire euclidien standard noté (·, ·). Un système de racines dans V est un ensemble fini de vecteurs non nuls (appelés racines) qui satisfont les propriétés suivantes :

La condition d'intégralité pour <α, β> force β à être sur les lignes verticales. En les combinant aux conditions d'intégralité pour <β, α> les possibilités pour les angles entre α et β sont encore réduites à au plus deux possibilités sur chaque ligne verticale.

1. Les racines engendrent V comme espace vectoriel.
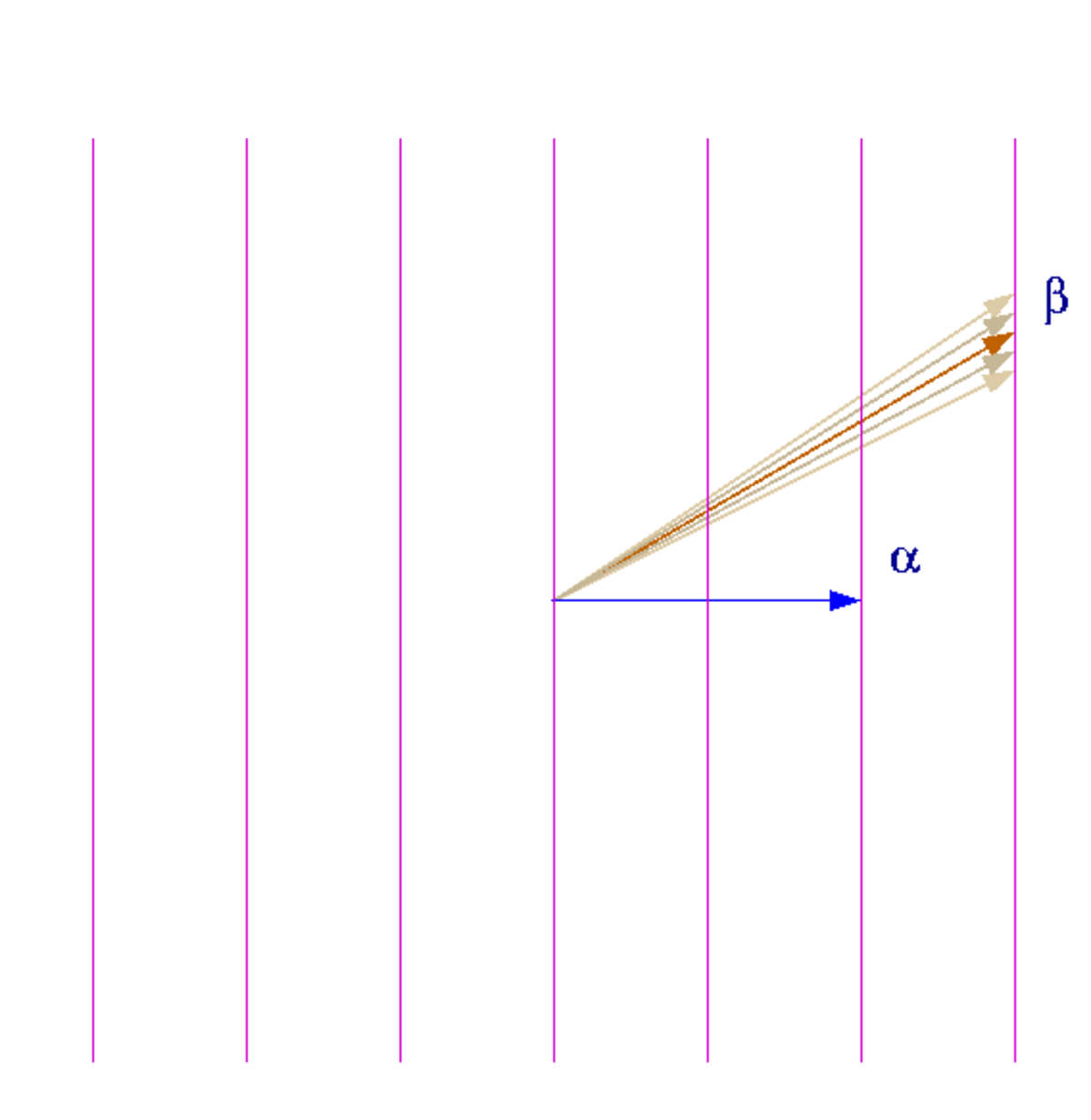
2. Les seuls multiples scalaires d'une racine qui sont dans sont elle-même et son opposé .
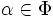
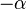
3. Pour chaque racine l'ensemble est stable par la réflexion à travers l'hyperplan perpendiculaire à i.e. pour toutes racines et on a,

   

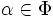
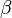
4. (condition d'intégralité) Si et sont des racines dans , alors la projection orthogonale de sur la ligne engendrée par est un multiple demi-intégral de  :

   

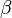
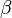
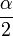
En raison de la propriété 3, la condition d'intégralité est équivalente à l'énoncé suivant : et son image par la réflexion par rapport à diffèrent par un multiple entier de .

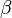
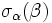
Le rang d'un système de racines est la dimension de V. On peut combiner deux systèmes de racines en faisant la somme directe des espaces euclidiens sous-jacents et en prenant l'union des racines. Un système de racines qui ne peut pas être obtenu de cette manière est dit irréductible.

Deux systèmes de racines et sont considérés comme identiques s'il existe une bijection entre qui envoie sur et préserve les rapports de distances.

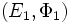
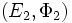
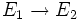
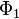
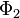
Le groupe des isométries de V engendré par les réflexions par rapport aux hyperplans associés aux racines de est nommé le groupe de Weyl de . Comme il agit fidèlement sur l'ensemble fini , le groupe de Weyl est toujours fini.

Racines positives et racines simples

Étant donné un système de racines , nous pouvons toujours choisir (de beaucoup de manières) un ensemble de racines positives. C'est un sous-ensemble de tel que

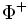
• pour chaque racine exactement une des racines est contenue dans
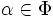
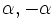
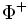
• Pour tout tel que est une racine, .

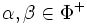
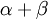
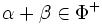
Si un ensemble de racines positives est choisi, les éléments de ( ) sont appelés racines négatives.

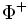
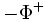
Le choix de est équivalent au choix des racines simples. L'ensemble des racines simples est un sous-ensemble de qui est une base de V avec la propriété spéciale que chaque vecteur dans lorsqu'il est écrit dans la base possède soit tous les coefficients ≥0 ou tous ≤0.

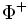
Il peut être montré que pour chaque choix de racines positives, il existe un unique ensemble de racines simples, c’est-à-dire que les racines positives sont exactement ces racines qui peuvent être exprimées comme une combinaison de racines simples avec des coefficients non-négatifs.