Théorème de Borsuk-Ulam - Définition
La liste des auteurs de cet article est disponible ici.
Démonstrations
Dimension un
En dimension un, la preuve est une conséquence directe d'un résultat analogue au théorème des valeurs intermédiaires. Soit f la fonction continue du cercle, choisi de centre le vecteur nul, dans R. On définit la fonction g du cercle dans R, qui à x associe g(x) = f(x) - f(-x). Le théorème revient à montrer que g possède un zéro. On remarque que la fonction g est impaire, c'est-à-dire que g(-x) = -g(x).
Soit x0 un point du cercle, si g(x0) est nul, le théorème est démontré. Dans le cas contraire, l'image de g est connexe car le disque l'est. Cette image contient donc le segment d'extrémités g(x0) et -g(x0). Ce segment contient 0, qui possède un antécédent.
Sous cette forme, le théorème n'est guère étonnant. Un corollaire est un peu plus surprenant, si deux fermés du cercle ont pour union le cercle entier, l'un des deux fermés contient deux points antipodaux. En effet, soit A et B les deux ensembles non vides et fermés dont l'union est égal au cercle. On considère la fonction f qui au point x du cercle, associe la distance de x à A. Le théorème assure l'existence de deux points x et -x ayant même image par f. Si cette image est 0, x et -x sont tous deux dans A, car A est fermé, et le corollaire est démontré. Dans le cas contraire, ils sont tous deux dans B et le corollaire est à nouveau démontré.
Dimension deux
Une méthode élégante, en dimension deux, fait appel au groupe fondamental du cercle. On raisonne par l'absurde et on suppose qu'il existe une fonction f de la sphère S2 dans R2 telle que tous les points antipodaux ont des images distinctes par f. On construit une fonction continue g de la sphère S2 dans le cercle S1. L'application g induit un morphisme g * du groupe fondamental de S2 dans S1. Comme S2 possède un groupe fondamental trivial car la sphère est simplement connexe, les images des lacets par g * devraient tous être homotopes à un point. On construit un lacet dont l'image ne l'est pas. Cette contradiction démontre le théorème. On définit la fonction g par :
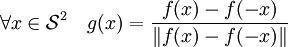
Comme on suppose qu'il n'existe aucun couple de points antipodaux ayant la même image par f, la fonction g est bien définie. On suppose que la sphère S2, tout comme le cercle S1 est de centre le vecteur nul et de rayon 1. On considère le lacet α de S2, qui à t associe le point de coordonnées (cos(2π.t), sin(2π.t), 0). Comme la fonction g est impaire, on dispose de l'égalité :
![(1)\quad \forall t \in [0,1/2]\quad g_*\alpha(t+ 1/2) = -g_*\alpha(t)](https://static.techno-science.net/illustration/Definitions/autres/7/7dd3182ea5c7eb27453db1549a9ce2f1_126d82a67ce7c2135082a24ca00b003b.png)
Par ailleurs, il existe une fonction p de [0, 1] dans R telle que le lacet g *α de S1 s'écrive :
![\forall t \in [0,1]\quad g_*\alpha(t) = (\cos(p(t)),\sin(p(t))\quad\text{avec}\quad p(0)=0](https://static.techno-science.net/illustration/Definitions/autres/b/b2ed93dd6e11e2493589cbd83b955291_fd4ee6b61bde6658c868651a3636ec2b.png)
La propriété (1) permet de déduire :
![\forall t \in [0,1/2]\quad 2\Big(p(t+1/2) - p(t)\Big) \in \Z](https://static.techno-science.net/illustration/Definitions/autres/8/815c36b0eb2e0a277a62d79dae79599f_485abd4abf53d2b98a604e17608c6c13.png)
La fonction, qui à t associe p(t + 1/2) + p(t) est continue, définie dans un ensemble connexe et à valeurs dans un ensemble discret, elle est donc constante. Cette constante est de la forme c/2 où c est un entier impair. Ce qui permet d'en déduire les égalités :
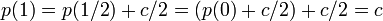
Le fait que c soit un entier impair montre que p(1) est un entier non nul et donc que g *α n'est pas homotope à un point. En fait, le lacet g *α fait c tours autour du cercle. Le morphisme g * est un morphisme de groupe trivial dans un groupe isomorphe à Z et possède une image différente de l'élément neutre. Cette impossibilité termine le raisonnement par l'absurde.

















































