Théorème de Borsuk-Ulam - Définition

Introduction

Stanislaw Marcin Ulam conjecture le théorème, mais ne parvient pas à le démontrer dans le cas général.

En mathématiques, le théorème de Borsuk-Ulam est un résultat de topologie algébrique. Il indique que pour toute fonction f continue d'une sphère de dimension n, c'est-à-dire la frontière de la boule euclidienne de Rⁿ⁺¹, dans un espace euclidien de dimension n, il existe deux points antipodaux, c'est-à-dire diamétralement opposés, ayant même image par f.

Pour D. Leborgne, il fait partie des « quelques grands théorèmes concernant la topologie des espaces de dimension finie ». Contrairement au théorème de Jordan, il est moins intuitif. Il indique, par exemple, qu'il existe deux points antipodaux de la Terre ayant exactement la même température et la même pression, et cela à chaque instant (même si ces points peuvent varier). On suppose ici que la température et la pression varient de manière continue.

Son premier usage concerne la topologie algébrique, il permet par exemple de démontrer le théorème du point fixe de Brouwer qui lui est analogue à certains égards. Il permet de démontrer des résultats au titre aussi amusant que la démonstration est difficile, comme le théorème du sandwich au jambon ou encore celui du partage du collier volé. A partir des années 1970, il devient un outil pour démontrer des résultats de purs dénombrement, liés à la théorie des graphes.

Ce théorème fut conjecturé par Stanislaw Marcin Ulam et prouvé par Karol Borsuk en 1933.

Énoncé

Corollaires

Partage d'une sphère

Si trois fermés recouvrent une sphère, l'un au moins contient deux points antipodaux.

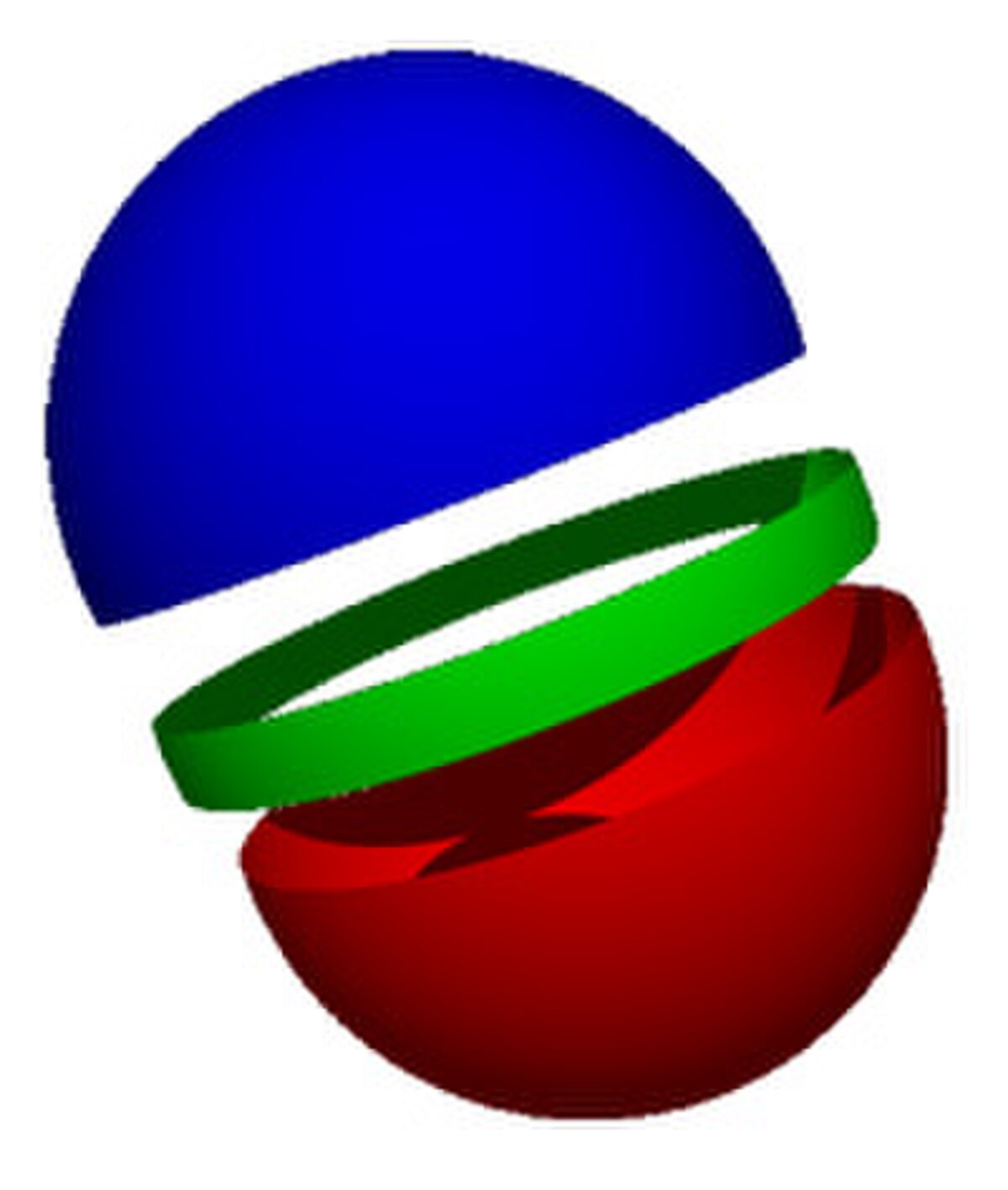
Le corollaire démontré pour le cercle se généralise. Cette fois-ci, la sphère est divisée en trois parties fermées comme illustré sur la figure de droite, la bleue, notée A, la rouge notée B et la verte C. Dans l'exemple, c'est la zone verte qui contient les points antipodaux. Une fois encore, le centre de la sphère est placé sur le vecteur nul, deux points antipodaux sont ainsi opposés.

On considère la fonction, qui à x, associe f(x) = (d_A(x), d_B(x)), la première coordonnée indique la distance séparant x de A et la deuxième celle qui sépare x de B. La fonction f est continue, le théorème de l'article assure l'existence de deux points antipodaux ayant même image par f. Si cette image comporte une coordonnée nulle, les points x et -x sont, soit dans A, soit dans B, car A et B sont fermés. Dans le cas contraire, x et -x sont nécessairement tout deux dans C.

On peut se demander si 3 est bien le nombre maximal pour décomposer une sphère en fermés contenant nécessairement deux points antipodaux dans un même fermé. Pour s'en persuader, le plus simple est de placer la sphère dans un tétraèdre régulier circonscrit à la sphère, comme illustré sur la figure de droite. On associe à chaque face du tétraède, un fermé de la sphère de la manière suivante. On considère un point p de la sphère et la demi droite d'extrémité le centre de la sphère et passant par p. Si cette demi droite rencontre une face du tétraèdre, le point p est élément du fermé associé à cette face (certains points de la sphère sont associés à deux faces si l'intersection est une arrête). Aucun des quatre fermés ne contient de couple de points antipodaux.

Le raisonnement proposé ici se généralise pour une dimension quelconque.

Théorème du sandwich au jambon

Le théorème du sandwich au jambon annonce l'existence d'un plan qui coupe chacun des trois solides en deux parties de volumes égaux.

Le théorème du sandwich au jambon dans le cas où n est égal à 3 s'exprime de manière suivante. Soit trois solides mesurables et bornés d'un espace euclidien de dimension trois. On les représente par deux tranches de pain et une tranche de jambon. Il existe un plan affine qui coupe chacune des trois figures en deux parties de volumes égaux. Plus généralement le théorème précise :

• Soit n parties bornées et Lebesgue-mesurables de l'espace réel euclidien de dimension n, il existe un hyperplan affine divisant chaque partie en deux morceaux de mesure égale.

Cette question est initialement posée par Hugo Steinhaus dans le cas de la dimension 3 en 1938 et est résolue par Stefan Banach. La réponse à cette question, d'apparence aussi ludique qu'anodine, est la clé de questions très sérieuses. Luis Paris remarque que : « .. c’est avec ces mêmes techniques que les mathématiciens ont établi l’existence d’enzymes appelées topo-isomérases qui effectuent des manipulations topologiques sur l'ADN ».

La démonstration est une conséquence directe du théorème de l'article. En dimension trois, la figure de droite illustre la preuve, avec pour solides, notés A, B et C, des solides de Platon en rouge. On considère une sphère de centre le vecteur nul et x un vecteur de la sphère. Pour chaque point p de la droite dirigé par x, il existe un plan orthogonal à x et passant par p. Si p varie continument, le volume de la zone du solide A qui se trouve dans le demi-espace placé du même côté que x, varie aussi continument. Ce demi-espace correspond à la zone qui n'est pas partiellement masqué par le plan illustré en jaune. Il existe une valeur de p, noté p_x telle que cette portion de volume soit exactement le moitié de celle de A. Soit f la fonction de la sphère qui associe à x deux réels, correspondant aux volumes des portions de B et C qui se trouvent dans le même demi-espace que celui considéré précédemment. La fonction f satisfait les conditions du théorème, il existe une valeur de x tel que f(x) soit égal à f(-x). Le plan orthogonal à x et passant par le point p_x vérifie la propriété annoncé par le théorème du sandwich au jambon. La démonstration se généralise aisément à une dimension quelconque.

Partage discret du collier

Le problème du partage discret du collier est beaucoup plus délicat à démontrer, même si son apparence est des plus simples. On présente souvent ce théorème en narrant l'histoire suivante : Deux voleurs dérobent un collier de valeur. Ce collier est composée de perles de t couleurs différentes (sur l'illustration de droite t est égal à 2). Le nombre de perles ayant l'une des t couleurs est toujours pair (dans l'exemple, on trouve 10 perles bleues et 10 vertes). Les deux malfrats souhaitent récupérer chacun le même nombre de perles pour chaque couleur. La chaîne étant en or, l'objectif est d'opérer le partage avec le minimum de coupes possibles. Le théorème indique que le nombre de coupes minimal ne dépasse jamais t.

Si t est égal à 2, deux coupes suffisent, la question peut-être vue comme une application du théorème de Borsuk-Ulam en dimension deux. Le premier solide est composé des perles bleus et le deuxième des perles vertes. Il existe une droite qui divise les deux solides en deux parties de volumes égaux. Ce résultat du théorème de l'article impose nécessairement une coupe passant par le milieu du collier. Cette coupe est illustrée sur la figure par la droite violette. Elle ne laisse pas nécessairement les perles intactes, mais les deux éventuelles perles coupées sont de même couleurs, car sinon chacun des deux voleurs recevrait non pas 5 perles bleues et 5 rouges, mais un nombre non entier de perles de chaque couleur. En pivotant l'axe violet pour que l'intersection de l'axe et du collier soit des points de la chaîne extérieurs aux perles, on obtient un axe de coupe (rouge sur la figure) qui répond à la question. On obtient bien deux coupes, qui sont les deux points d'intersection de l'axe rouge et du collier.

Si t est quelconque, la question est plus ardue, même si la réponse est conjecturée depuis longtemps. C'est en 1986 que le théorème est démontré pour la première fois. La démonstration est considérablement simplifiée l'année suivante. L'usage du théorème de Borsuk-Ulam est à l'origine de cette simplification. Le cas où le nombre de voleurs n'est pas 2 mais devient une valeur q quelconque, devient accessible. Il est traité l'année suivante par l'un des auteurs de la démonstration précédente, il faut t(q - 1) coupes, généralisant le résultat précédent. Les preuves sont néanmoins trop sophistiquées pour être présentées ici.

A la différence des exemples précédents, le théorème de l'article quitte ici son champ d'application naturelle : la topologie algébrique, pour devenir la cheville ouvrière d'un résultat de dénombrement.