Groupe fondamental - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, et plus spécifiquement en topologie algébrique, le groupe fondamental, ou groupe de Poincaré, est un invariant topologique. Le groupe fondamental d'un espace topologique pointé (X, p) est, par définition, l'ensemble des classes d'homotopie de lacets (arcs fermés) de X d'origine et d'extrémité p. C'est un groupe dont la loi de composition interne est induite par la concaténation des arcs.
L'examen des groupes fondamentaux permet de prouver que deux espaces ne peuvent être homéomorphes, ou topologiquement équivalents. Le groupe fondamental permet de classifier les revêtements d'un espace connexe par arcs, à un isomorphisme près.
Une généralisation des groupes fondamentaux est la suite des groupes d'homotopie supérieurs. Pour cette raison, le groupe fondamental est aussi appelé premier groupe d'homotopie.
Le groupe fondamental fut introduit par Henri Poincaré dans la douzième section de son article intitulé Analysis Situs, paru en 1895 et annoncé dans une note aux Comptes-rendus de l'Académie des Sciences, parue en 1892.
Définition intuitive à travers l'exemple du tore
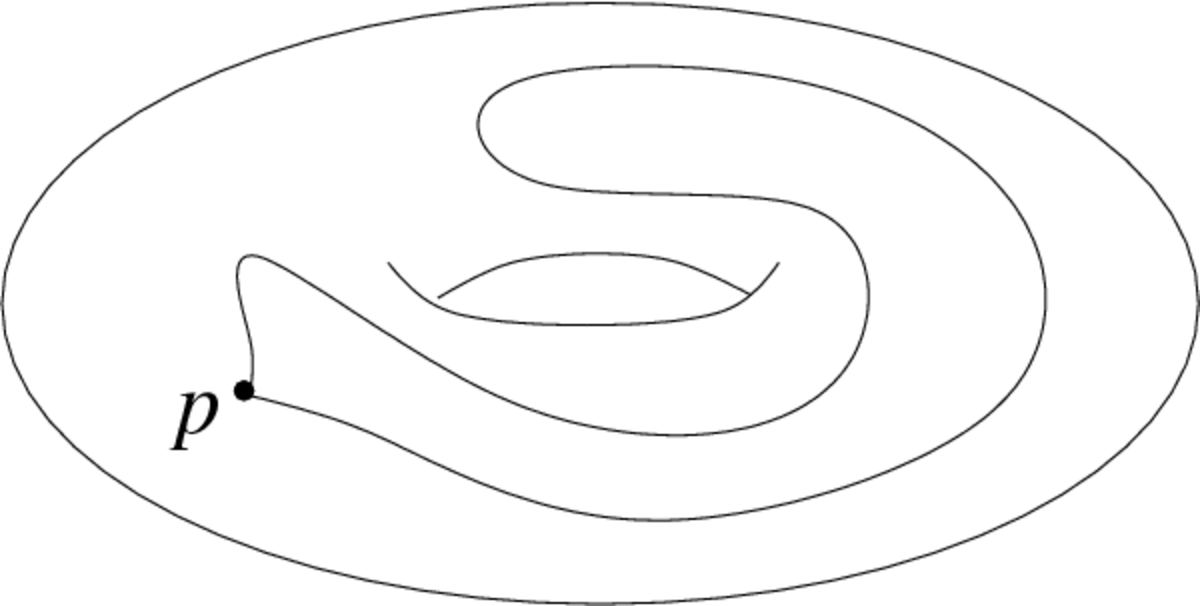
Tout d'abord, familiarisons-nous avec l'idée du groupe fondamental à travers l'exemple du tore bidimensionnel (qu'on peut se représenter comme étant la surface d'un donut ou d'une bouée). On fixe sur le tore un point de départ p.
À partir de ce point, on peut construire des lacets, i.e des courbes fermées, qui partent du point p, se promènent sur le tore et qui reviennent au point de départ. Imaginons que les lacets soient faits à partir de caoutchouc comme un élastique et qu'il soit ainsi possible de les étirer, les déformer de telle manière que le point de départ et le point d'arrivée soient toujours p et que les lacets se déplacent toujours sur le tore. Une telle déformation s'appelle une homotopie : on dit que deux lacets qui peuvent s'obtenir l'un à partir de l'autre par une homotopie sont homotopiquement équivalents. Ce sont les lacets à déformation près qui nous intéressent : on regroupe donc les lacets dans des classes d'homotopie. Le groupe fondamental du tore est l'ensemble des différentes classes d'homotopie des lacets.
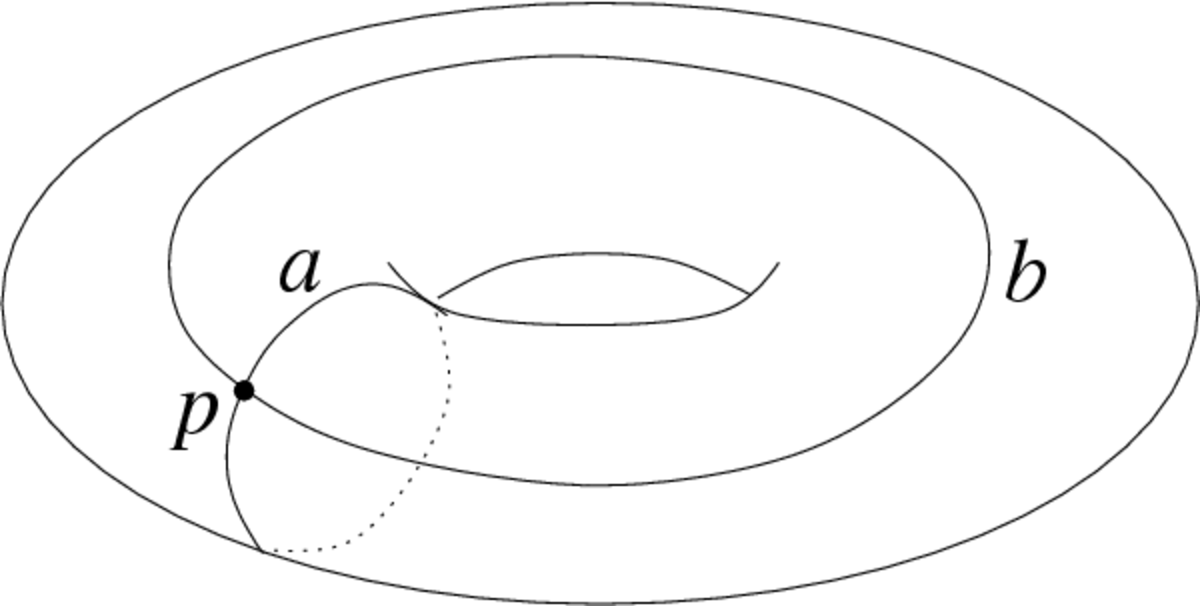
Dans la figure ci-contre, les lacets a et b ne sont pas homotopiquement équivalents : on ne peut obtenir l'un en déformant continûment le second sans le « déchirer » à un moment, ils représentent deux éléments distincts du groupe fondamental. On obtient d'autres classes d'homotopie en faisant tourner les lacets plusieurs fois autour du trou.
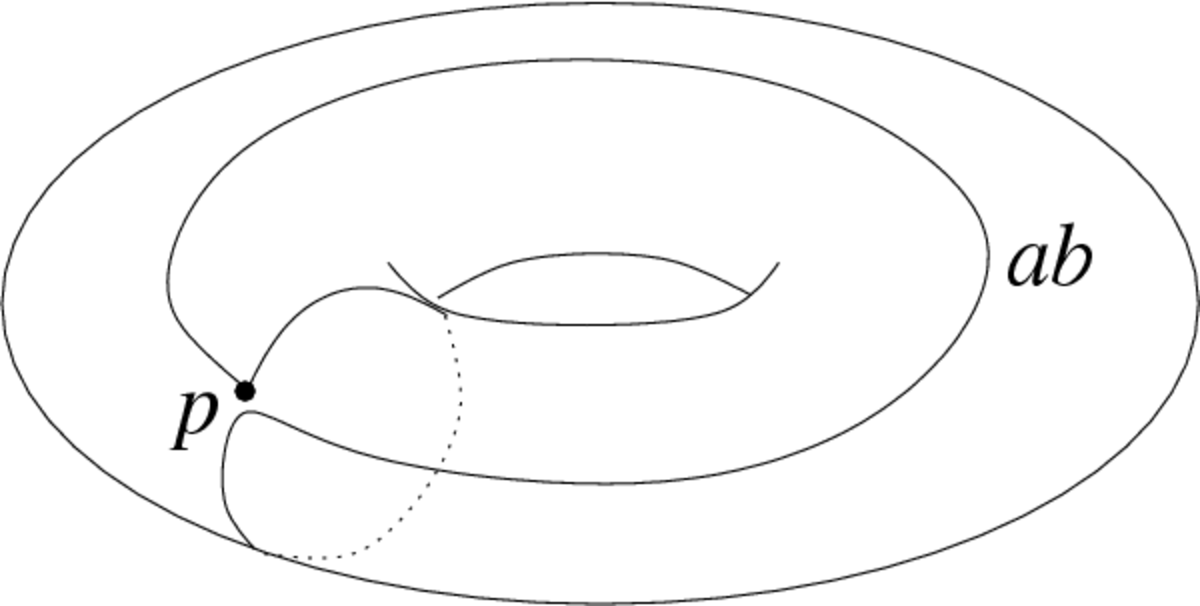
Comme son nom l'indique, le groupe fondamental n'est pas un simple ensemble, il est muni d'une structure de groupe : la loi de composition interne est celle qui à deux lacets associe un troisième lacet obtenu en parcourant le premier puis le second à la même vitesse (il n'y a pas de problèmes de définition puisque les lacets commencent et terminent avec le même point p). L'élément neutre du groupe fondamental est la classe d'homotopie du lacet qui reste au point p. On obtient un élément inverse en parcourant les lacets d'une classe d'homotopie dans le sens contraire.
Exemples
Convexes d'un espace euclidien
Soit E un espace euclidien de dimension n, où n est un entier strictement positif. On dispose de la propriété suivante :
-
- Le groupe fondamental d'un ensemble convexe C non vide de E est trivial. Autrement dit, un convexe d'un espace euclidien (plus généralement d'un espace vectoriel topologique localement convexe) est simplement connexe.
Si p est un élément de C, l'objectif est de montrer que π1(C,p) est le groupe trivial, ou encore que tout lacet γ basé en p est homotope au point p, c'est-à-dire au lacet constant valant p. Pour cela on définit une application H : [0 1]2 → C définie par :
L'application H est manifestement continue, comme γ(x) et p sont deux éléments de C, pour toutes valeurs de t H(t,x) est élément de C car C est convexe. L'application H définit bien une homotopie entre le lacet constant et γ.
Cercle
Le terme de cercle désigne ici un espace homéomorphe à l'ensemble des points situées à une distance constante non nulle d'un point c d'un plan euclidien. Ainsi, l'ensemble des nombres complexes de module 1 ou encore R/Z sont des cercles. Le cercle est noté ici S1 et est identifié aux nombres complexes de module 1.
-
- Le groupe fondamental du cercle est isomorphe à Z l'ensemble des nombres entiers.
Intuitivement, ce résultat est évident. On considère ici π1(S1,1), c'est-à-dire que le point de base est 1. Si le chemin considéré fait n tours dans le sens trigonométrique, on a envie de lui associer par l'isomorphisme de groupe μ de Z dans π1(S1,1) qui, à la valeur m, associe une classe de lacets qui fait m tours, dans le sens trigonométrique si m est positif, et dans le sens inverse sinon. Pour construire l'isomorphisme μ, on définit les lacets em de la manière suivante :
On définit μ comme l'application qui à m associe [em]. Intuitivement, il semble clair que μ est un isomorphisme.
La non trivialité du groupe fondamental du cercle est à l'origine de plusieurs démonstrations de théorèmes non triviaux. Un exemple est celui de Borsuk-Ulam qui indique qu'une application continue de la sphère dans le plan possède toujours deux points antipodaux ayant même image. Ce résultat est la clé de la démonstration du théorème du sandwich au jambon qui indique qu'il existe toujours un plan qui divise deux parties de volumes égaux trois solides bornés et mesurables.
La méthode de démonstration consiste à construire l'inverse de μ : ν de π1(S1,1) dans Z tel que ν([e1]) soit égal à 1. Une fois cet inverse construit, on montre que c'est un morphisme de groupes définie sur les lacets simples d'extrémités 1 et qu'il respecte la relation d'équivalence définissant l'homotopie. On montre ensuite son caractère bijectif.
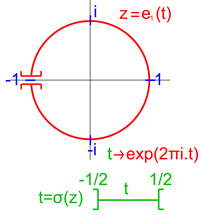
On définit pour cela une application p de R dans S1 par :
Pour établir un lemme, nécessaire à la démonstration, une remarque est utile. La restriction de e1 à l'intervalle ]-1/2, 1/2[ est un homéomorphisme à valeurs dans S1 − { − 1}, il est illustré sur la figure de droite. Le caractère bijectif est évident, la restriction est continue et son inverse σ est continu car défini par :
-
- Soit α une application de [0, 1] dans S1 dont l'image de 0 soit égale à 1. Il existe une unique application continue, nulle en 0 de β de [0, 1] dans les nombres réels, telle que la composée poβ soit égale à α :
Établissons l'unicité de β. Pour cela, on suppose qu'il existe deux applications β1 et β2 qui vérifient la proposition, on va montrer qu'elles sont égales, ou plus exactement que leur différence est nulle. Cette différence est une application continue, égale à 0 en 0, définie sur un connexe et à valeurs dans un ensemble discret (en l'occurrence Z). Une telle application est nécessairement nulle.
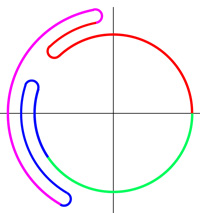
Montrons son existence. Si α est à valeurs dans S1 − { − 1}, le fait que σ soit un homéomorphisme permet de conclure. Si ce n'est pas le cas, on procède par découpage de l'intervalle [0, 1]. L'application α est définie sur un compact et est continue, elle est donc uniformément continue, ce qui montre l'existence d'un réel strictement positif r tel que :
Autrement dit, si t2 ne s'éloigne de t1 de strictement moins que r, le rapport α(t2) / α(t1) n'atteint jamais la valeur -1 sur laquelle σ n'est pas définie. Cette propriété permet de définir la fonction β par étapes. Soit M un entier strictement positif tel que 1/M soit strictement plus petit que r. Sur l'intervalle [0, 1/M], on définit la fonction β comme égale à σoα. On dispose des égalités
Soit k un entier compris entre 1 et M − 1, et αk = α(k / M) − 1. Sur l'intervalle [k/M, (k + 1)/M], la fonction qui à t associe αk.α(t) vaut 1 en k/M et ses images ne quittent jamais le domaine de définition de σ. Cette situation est illustrée sur la figure de droite, sur chaque segment, le lacet est illustré d'une couleur différente, aucun segment ne s'éloigne d'exactement un demi-tour du point d'origine. Ce qui permet de définir β sur cet intervalle par :
Par construction, la fonction β est continue et vérifie bien par récurrence sur k, que l'égalité recherchée :
On suppose maintenant que α est un lacet, on définit l'application ν comme celle qui à α associe l'extrémité β(1), qui correspond intuitivement au nombre de tours effectué par α. Comme α(1) est égal à 1, on en déduit que ν(α) est nécessairement un entier. Montrons maintenant que c'est un morphisme de groupe :
-
- Soient α1 et α2 deux lacets de S1 d'extrémités 1, l'égalité suivante est vérifiée :
On note α le lacet α1.α2. Par définition du lacet α, et avec les notations évidentes :
La valeur ν(α1) est entière. on en déduit, par continuité de β :
Il faut encore montrer que l'application ν est compatible avec l'homotopie. Un premier lemme est utile.
-
- Si deux lacets α1 et α2 de S1 et d'extrémités 1 vérifient la majoration suivante, ils ont même image par ν :
On considère l'application quotient : αc = α1 / α2, son image est incluse dans S1 − { − 1}, c'est-à-dire le domaine de définition de σ. On en déduit, avec les notations usuelles :
On remarque que :
Ce qui montre que les fonctions δ et β2 sont confondues. La fonction βc prend ses images dans l'intervalle ]-1/2, 1/2[, ce qui montre que la différence entre β1 et β2 est toujours, en valeur absolue, strictement plus petite que 1. Au point 1, les deux fonctions diffèrent d'une valeur entière, qui ne peut que être nulle. Cette remarque termine la démonstration du lemme.
-
- Soient α1 et α2 deux lacets de S1 d'extrémités 1 et homotopes. Ils ont même image par ν :
Dire que les lacets sont homotopes revient à dire qu'il existe une application continue H(t, x) de [0, 1]2 et à valeurs dans S1 tel que l'application H(t, 0) soit égale à α1 et H(t, 1) soit égale à α2. L'application H est uniformément continue, car continue et définie sur un compact, il existe donc un entier M tel que :
On note δk, pour k entier variant de 0 à M, l'application qui à t associe H(t, k/M). Les applications δk sont toutes des lacets d'extrémités 1, le lemme précédent montre qu'elles sont toutes homotopes. Il suffit alors de remarquer que δ0 est égal à α1 et que δM est égal à α2 pour conclure.
-
- Conclusion :
Le passage au quotient montre que ν est bien un morphisme de groupe de π1(S1,1) dans Z. On remarque que ν([e1] est bien égal à 1, un générateur de Z, ce qui montre que le morphisme est surjectif. Il reste encore à montrer que ν est injectif. Soit α un élément de son noyau. Par définition l'application β est un lacet de R (qui vaut 0 en 0 par construction et 0 en 1 car α est élément du noyau de ν. Comme R est simplement connexe, ce lacet est homotope à au point 0. Soit F(t, x) une application continue de [0, 1]2 dans R telle que l'application t → F(t, 0) soit égal à β et t → F(t, 1) la fonction constante nulle. Une telle fonction existe car β est homotope au point 0. On construit la fonction H de [0, 1]2 dans S1 de la manière suivante :
La fonction H est continue et montre que [α] est bien la classe nulle, d'où l'injectivité de ν. On a établi que l'application ν est un morphisme bijectif de groupe, ce qui termine la démonstration.
Espace produit
Si X et Y sont deux espaces connexes par arcs, l'espace topologique produit XxY est aussi connexe par arcs. Si (p, q) est un point du produit, le groupe fondamental de XxY que l'on note π1(XxY,(p,q)) est bien défini. On dispose de la propriété suivante :
-
- Le groupe fondamental de l'espace produit XxY est le produit direct du groupe fondamental de X par celui de Y.
Les propositions précédentes permettent d'établir que le produit S1 par lui-même, généralement appelé tore de dimension 2, admet un groupe fondamental isomorphe à Z2. Plus généralement, le groupe fondamental du tore de dimension n est isomorphe à Zn.
Soit Px (resp. Py), la projection canonique de XxY dans X (resp. Y). À un lacet α, on associe αx (resp. αy) le lacet défini par la composition Pxoα (resp. Pyoα). On remarque que cette application respecte la relation d'équivalence de l'homotopie car les deux projecteurs sont continus. Il est donc possible de définir les applications μ1 et μ2 du groupe fondamental de XxY dans le groupe fondamental de X et de Y qui à [α] associe [αx] et [αy].
Ces deux applications sont manifestement des morphismes surjectifs de groupes. Établir la bijectivité de μ1xμ2 est un simple jeu d'écriture.
Autres exemples
- Pour
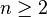
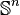
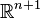
- Le groupe fondamental peut également contenir des éléments de torsion : par exemple, le groupe fondamental du plan projectif
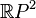
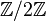
- Le groupe fondamental n'est pas toujours commutatif : Par exemple, le groupe fondamental basé en un point p du plan privé de deux points
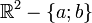
- En fait, on peut montrer que pour n'importe quel groupe G, il existe un espace topologique de groupe fondamental G. (On peut en fait trouver un CW-complexe de dimension 2 ou même une variété de dimension 4 si le groupe est de présentation finie).
![\forall t,x \in [0,1]\quad H(t,x)= tp + (1-t)\gamma(x)](https://static.techno-science.net/illustration/Definitions/autres/2/228256d843bcbac96035f24b53923f59_f47870c852f11ba1311177a66548eb61.png)
![e_m : [0,1] \rightarrow \mathbb S^1\quad e_m(t) = \exp(2i\pi mt)](https://static.techno-science.net/illustration/Definitions/autres/9/995265c0011c7f3bd7ea43bb26a4af1f_fb982d665c671e0902639cd49d07754d.png)
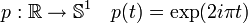
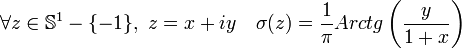
![\forall t_1,t_2 \in [0,1]\quad |t_1-t_2| < r \Rightarrow |\alpha(t_1) - \alpha(t_2)\|<2 \text{ ou encore } \left|\frac {\alpha(t_2)}{\alpha(t_1)} - 1\right|<2 \text{ car } |\alpha(t_1)| = 1](https://static.techno-science.net/illustration/Definitions/autres/8/8b5586ea203cdefe49d29eefacb6a093_ff837d4e2c91f56921fa176c9ff73865.png)
![\forall t \in [0, 1/M] \quad \beta(t) = \sigma\circ \alpha (t) \quad \text{et}\quad p\circ \beta(t) = \alpha(t)](https://static.techno-science.net/illustration/Definitions/autres/0/0f693766f5bdb59c62a9939098b96d74_88797218db7b93271d6fc383b589dab6.png)
![\forall t \in [k/M, (k+1)/M]\quad \beta(t) = \sigma\left(\alpha_k \alpha (t)\right) + \beta(k/M)](https://static.techno-science.net/illustration/Definitions/autres/5/51d153a9e79e1ae19b86cc343831a06d_7bf1053c372cfc14f291feea924f2895.png)
![\forall t \in [k/M, (k+1)/M]\quad p\circ\beta(t) = p\circ(\sigma\left(\alpha_k \alpha (t)\right))\cdot p\circ \beta(k/M) = \alpha_k\alpha(t)\alpha(k/M) = \alpha(t)](https://static.techno-science.net/illustration/Definitions/autres/7/71feb63cd903f6810045d663cb12c4e0_143cddf967617bff3c383c50922ef4d0.png)
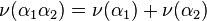
![\forall t \in [0,1/2]\quad \alpha(t) = \alpha_1(2t) = p\circ\beta_1(2t) = p\circ \beta(t) \quad \text{et}\quad \beta(1/2) = \beta_1(1)=\nu(\alpha_1)](https://static.techno-science.net/illustration/Definitions/autres/1/10d638c7066f2aaf1780745a634f2e4c_cab779f26a7a8becd5206891ea0cdc31.png)
![\forall t \in [0,1/2]\quad \alpha(1/2+t) = \alpha_2(2t) = p\circ(\nu(\alpha_1)+\beta_2)(2t)\quad \text{et}\quad \beta(1) = \beta_1(1) + \beta_2(1)=\nu(\alpha_1)+\nu(\alpha_2)](https://static.techno-science.net/illustration/Definitions/autres/5/532eae6d4fbd4eb705c5f4896276cbf9_5cc9ce3e73191cffa93908b6d9ff01ea.png)
![\forall t \in [0,1]\quad |\alpha_1(t) - \alpha_2(t)|< 2](https://static.techno-science.net/illustration/Definitions/autres/4/4a9a4b97dda0bf1ae9c9fcde30a97678_56d25b7d58e72ed513f1a13f8fc8f062.png)
![\forall t \in [0,1]\quad \beta_c(t) = \sigma\circ \alpha_c(t)\quad\text{Notons}\quad \delta(t) = \beta_1(t) + \beta_c(t)](https://static.techno-science.net/illustration/Definitions/autres/8/8448f3239ec9c5597e76461971a56bef_af1b2957b14aeb5d63d19bacfd1441fa.png)
![\forall t \in [0,1]\quad p\circ\delta(t) = \frac {p\circ \beta_1(t)}{p\circ \beta_c(t)}= \alpha_2(t)](https://static.techno-science.net/illustration/Definitions/autres/1/12834be5c5804fd42228d834369100ad_e7a12a8c010f24e6b7698d51877fbb29.png)
![\forall k \in \{1,\cdots M\},\; \forall t \in [0,1] \quad |H(t,(k-1)/M)-H(t,k/M)|<2](https://static.techno-science.net/illustration/Definitions/autres/f/f34c3d8c8db887ad1ed3523d9681fc0f_1f81bd6eee6b71e10b6ec93f636629e8.png)
![\forall t,x \in [0,1],\quad H(t,x) =p\circ F(t,x)](https://static.techno-science.net/illustration/Definitions/autres/4/446a62b7c80d72dba9ae140dba3e5931_d336b5f8dd7867b54849cd00a2ee8592.png)