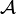Théorème de Hille-Yosida - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Semi-groupes - Théorème de Hille-Yosida - Opérateurs dissipatifs - Exemples

Opérateurs dissipatifs

Définitions

Un opérateur $(A, D (A))$ est dissipatif si $\forall x\in D(A) \text{ et } \forall \lambda >0, ~ ||x-\lambda Ax|| \geq ||x||$ . Dans le cas où $X = H$ est hilbertien on montre que $A$ est dissipatif si et seulement si $\forall x\in D(A) ~ \mathfrak{Re}(<Ax,x>_H) \leq 0$ .

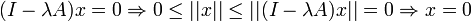
Remarque: Si $(A, D (A))$ est un opérateur dissipatif alors $\forall \lambda > 0$ l'opérateur $(I d - λ A)$ est injectif car $(I-\lambda A)x = 0 \Rightarrow 0 \leq ||x|| \leq ||(I-\lambda A)x||=0 \Rightarrow x= 0$ .

Si de plus $\forall \lambda >0, ~ Id - \lambda A$ est surjectif on dit que $(A, D (A))$ est maximal-dissipatif (ou m-dissipatif). On peut montrer que $\forall \lambda >0, ~ Id - \lambda A ~ \text{surjectif} \Leftrightarrow \exists \lambda_0 ~ tq ~ Id - \lambda_0 A ~ \text{surjectif}$ . En pratique pour montrer qu'un opérateur est m-dissipatif on montre d'abord à la main qu'il est dissipatif et on résout ensuite un problème variationnel pour une valeur $λ 0$ bien choisie (par exemple avec le théorème de Lax-Milgram, voir exemple de l'équation de la chaleur traité plus bas).

Dans ce cas l'opérateur $(I d - λ A)$ est un isomorphisme (a priori non continu) de $L (A, X)$ et on note $J λ = (I d - λ A) - 1$ . De plus, comme $||J_{\lambda}y||_X \leq ||(Id-\lambda A)[J_{\lambda}y]||_X \leq ||y||_X$ , $J_{\lambda} \in \mathcal{L}\left((X,||.||_X),(D(A),||.||_X)\right)$ . Nous allons voir que cette propriété de continuité peut être améliorée (on va rendre moins fine la topologie sur $(D (A), | | . | | X)$ en munissant $D (A)$ d'une norme $| | . | | D (A)$ ).

Propriétés des opérateurs m-dissipatifs

Prop 1: si $(A, D (A))$ est m-dissipatif alors c'est un opérateur fermé.

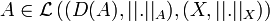
Corollaire 1: pour $x \in D(A)$ on pose $| | x | | D (A) = | | x | | X + | | A x | | X$ . Alors $| | . | | D (A)$ est une norme pour laquelle $D (A)$ est un espace de Banach et $A \in \mathcal{L}\left((D(A),||.||_A),(X,||.||_X)\right)$ .

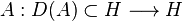
Prop 2: si $H$ est un espace Hilbertien et $A : D(A) \subset H \longrightarrow H$ est m-dissipatif alors il est à domaine dense.

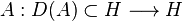
Prop 3: réciproquement si $A : D(A) \subset H \longrightarrow H$ est de domaine dense, dissipatif, fermé et tel que son adjoint $(A *, D (A *))$ est dissipatif alors $(A, D (A))$ est m-dissipatif.

Corollaire 3: toujours dans le cadre hilbertien

(i)

(A, D (A))

est dissipatif autoadjoint à domaine dense alors il est m-dissipatif

(i i)

(A, D (A))

est anti-adjoint à domaine dense alors il est m-dissipatif

Remarque: dans $(i i)$ la condition de dissipativité n'est pas nécessaire car $(A, D (A))$ anti-adjoint entraîne que $< A x, x > H = 0$ donc la dissipativité, voir l'exemple de l'équation des ondes plus bas.

Exemples

L'équation de la chaleur

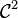
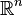
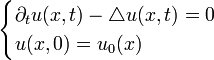
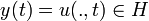
On se donne $Ω$ un ouvert borné de classe $\mathcal{C}^2$ de $\mathbb{R}^n$ et on cherche à résoudre l'équation de la chaleur $\begin{cases} \partial_t u(x,t) - \triangle u(x,t)=0 \\ u(x,0) = u_0(x) \end{cases}$ sur $(x,t)\in \Omega \times [0,+\infty]$ pour une condition initiale donnée. 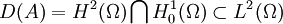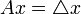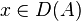On peut réécrire cette EDP sous la forme d'une EDO $y'(t) = A y (t)$ en posant $X = H = L 2 (Ω)$ , $y(t)=u(.,t)\in H$ et en définissant $(A, D (A))$ par $D(A)=H^2(\Omega) \bigcap H^1_0(\Omega) \subset L^2(\Omega)$ et $Ax=\triangle x$ pour tout $x \in D(A)$ . Nous sommes dans le bon cadre pour utiliser la théorie des semi-groupes et le théorème de Hille-Yosida; reste à montrer que l'opérateur A est m-dissipatif. Il est bien connu que le laplacien est un opérateur autoadjoint (on a $<Au,v>_H=\int_{\Omega}(\triangle u)v = -\int_{\Omega}\nabla u . \nabla v=\int_{\Omega}u(\triangle v ) = <u,Av>_H$ par double intégration par parties) et que $D (A)$ est dense dans $L 2 (Ω)$ , il suffit donc de montrer qu'il est dissipatif ou de façon équivalente que $\mathfrak{Re}(<Ax,x>_H) \leq 0$ . 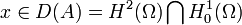Or tout $x \in D(A)=H^2(\Omega) \bigcap H^1_0(\Omega)$ est de trace nulle, donc en intégrant par parties $\mathfrak{Re}(<Ax,x>_H)=-\int_{\Omega}||\nabla x||^2_{\mathbb{R}^n} \leq 0$ . Le corollaire 3 et le théorème de Hille-Yosida permettent enfin de conclure quant à l'existence-unicité et la régularité des solutions. Remarquer que $\frac{d}{dt}\left(||y(t)||^2_H\right)=2<y'(t),y(t)>_H=2<Ay(t),y(t)>_H \leq 0$ : on retrouve bien sur le côté dissipatif et irréversible de l'équation de la chaleur.

L'équation des ondes

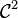
L'équation des ondes homogène se formule dans un domaine $Ω$ suffisamment régulier (c'est-à-dire $\mathcal{C}^2$ en pratique) et sur un intervalle de temps $[0, T)$ (avec $T > 0$ ) selon

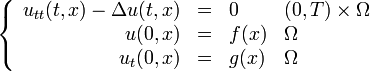
$\left\{\begin{array}{rcll}u_{tt}(t,x) -\Delta u(t,x) & = & 0 & (0,T) \times \Omega\\ u(0,x) & = & f(x) & \Omega\\ u_{t}(0,x) & = & g(x) & \Omega \end{array}\right.$

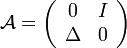
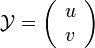
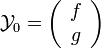
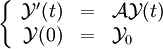
On se place dans la théorie des semi-groupes en mettant l'équation précédente au premier ordre en temps. On pose alors $\mathcal{A} = \left(\begin{array}{cc} 0 & I \\ \Delta & 0 \end{array}\right)$ , $\mathcal{Y} = \left(\begin{array}{c} u \\ v \end{array}\right)$ (avec $v = u'$ ) et $\mathcal{Y}_0 = \left(\begin{array}{c} f \\ g \end{array}\right)$ l'équation devient alors $\left\{\begin{array}{rcll} \mathcal{Y}'(t) & = & \mathcal{A}\mathcal{Y}(t) \\ \mathcal{Y}(0) & = & \mathcal{Y}_0 \end{array}\right.$ .

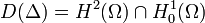
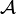
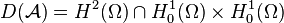
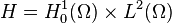
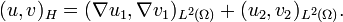
Le domaine du Laplacien étant $D(\Delta) = H^2(\Omega) \cap H_0^1(\Omega)$ , celui de $\mathcal{A}$ est $D(\mathcal{A}) = H^2(\Omega) \cap H_0^1(\Omega) \times H_0^1(\Omega)$ sur $H = H_0^1(\Omega) \times L^2(\Omega)$ . Les conditions initiales seront alors prises dans $H$ . Le produit scalaire dans $H$ est défini pour tout couple $(u, v)$ dans $H$ ( $u = (u 1, u 2)$ et $v = (v 1, v 2)$ ) par $(u,v)_H = (\nabla u_1,\nabla v_1)_{L^2(\Omega)} + (u_2,v_2)_{L^2(\Omega)}.$

Reste à vérifier que nous sommes bien dans les conditions d'application du théorème de Hille-Yosida :

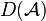
$D(\mathcal{A})$ est dense dans $H$ .
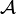
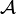
$\mathcal{A}$ est fermé.
$\mathcal{A}$ est dissipatif. Ce point mérite une preuve.

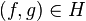
Preuve 1. On utilise la caractérisation $(i')$ du théorème. Soient $λ > 0$ et $(f,g) \in H$ . L'équation résolvante s'écrit en $(u, v)$

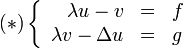
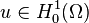
$(*)\left\{ \begin{array}{rcl} \lambda u - v & = & f \\ \lambda v - \Delta u & = & g \end{array} \right.$ d'où $(λ 2 I - Δ) u = λ f + g$ qui admet une unique solution dans $u \in H^1_0(\Omega)$ via Lax-Milgram (car d'une part $λ 2 > 0$ et d'autre part les valeurs propres du Laplacien sont strictement négatives donc $(λ 2 I - Δ)$ est un opérateur elliptique dont la forme bilinéaire associée vérifie les hypothèses du théorème de Lax-Milgram). 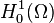Et alors $v = λ u - f$ est dans $H_0^1(\Omega)$ .

L'estimation de l'opérateur résolvant $R λ$ vient du produit scalaire de $( * ) 2$ par $v$ en remplaçant $u$ par sa valeur dans $( * ) 1$ :

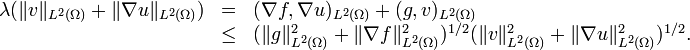
$\begin{array}{rcl} \lambda (\|v\|_{L^2(\Omega)} + \|\nabla u\|_{L^2(\Omega)}) & = & ( \nabla f,\nabla u)_{L^2(\Omega)} + (g, v)_{L^2(\Omega)} \\ & \leq & (\|g\|_{L^2(\Omega)}^2 + \|\nabla f\|_{L^2(\Omega)}^2)^{1/2}(\|v\|_{L^2(\Omega)}^2+\|\nabla u\|_{L^2(\Omega)}^2)^{1/2}. \end{array}$

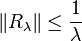
D'où, puisque $(u, v) = R λ (f, g)$ , on obtient l'estimation attendue $\|R_\lambda\| \leq \frac{1}{\lambda}$ . Le semi-groupe engendré par $\mathcal{A}$ est donc un semi-groupe de contraction.

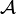
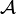
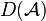
Preuve 2. On peut utiliser le Corollaire 3 pour montrer que $\mathcal{A}$ est m-dissipatif en montrant que $\mathcal{A}$ est anti-adjoint. On a alors pour tout couple $(u, v)$ dans $D(\mathcal{A})$

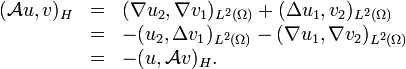
$\begin{array}{rcl} (\mathcal{A}u,v)_H & = & (\nabla u_2,\nabla v_1)_{L^2(\Omega)} + (\Delta u_1,v_2)_{L^2(\Omega)} \\ & = & -(u_2,\Delta v_1)_{L^2(\Omega)} - (\nabla u_1,\nabla v_2)_{L^2(\Omega)} \\ & = & -(u,\mathcal{A}v)_H. \end{array}$

Ainsi, $\mathcal{A}$ est anti-adjoint et à domaine dense donc m-dissipatif.

Théorème de Hille-Yosida

- Introduction - Semi-groupes - Théorème de Hille-Yosida - Opérateurs dissipatifs - Exemples

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️

Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜

Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️

Cette vitamine développe les fonctions cognitives du cerveau 🧠

Comment des impacts géants vaporisent les corps planétaires ☄️

Les Américains riches vivent moins longtemps que les Européens pauvres 💰

Attention à ce riz naturellement riche en arsenic 🍚

L'intelligence artificielle contre la mort subite 💀

L'inévitable formation d'un océan de magma basal sur Terre 🔥

Découverte d'une plante étrange sans chlorophylle 🌱

Existe-t-il des mélodies naturelles ? 🎶

Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽

L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡

Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺

Imprimer en 3D avec la lumière du soleil ☀️

La pollution atmosphérique nuit gravement au cerveau 🧠

Le trou noir supermassif Ansky vient de se réveiller ⚫

Voici ce qui rend notre cerveau vraiment unique 🧠

Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩

Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬

La physique révèle les secrets d'un strike parfait au bowling 🎳

Le TDAH associé à la démence 🧠

Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️

Le régime cétogène montre des surprises sur le cholestérol 🧐

Un tango observationnel révèle une Super-Terre 🔭

Cette expérience montre que la graisse brune augmente fortement la longévité 🕒

Page générée en 0.116 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise