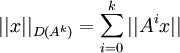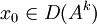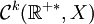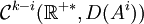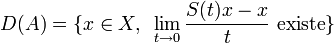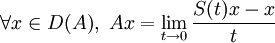Théorème de Hille-Yosida - Définition

Introduction

En théorie des semi-groupes, le théorème de Hille-Yosida est un outil puissant et fondamental reliant les propriétés de dissipation de l'énergie d'un opérateur non borné à l'existence-unicité et la régularité des solutions d'une équation différentielle (E) .

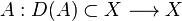
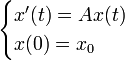
Semi-groupes

La théorie des semi-groupes doit son origine à l'étude du flot d'une équation différentielle ordinaire autonome en dimension finie ainsi que de l'exponentielle d'opérateurs.

Définitions

• Soit X un espace de Banach; on dit que la famille d'opérateurs linéaires est un semi-groupe (fortement continu) si :

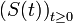
(i)

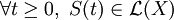
(ii)

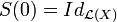
(iii)

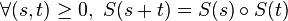
(iv)

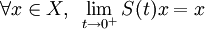
La condition (iv) est équivalente à ce que . Si on remplace (iv) par (iv) ^*: on dit que est uniformément continu.

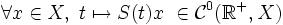
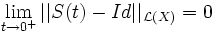
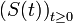
On retrouve (vaguement) avec cette définition la notion de famille à un paramètre de difféomorphismes bien connue en théorie des EDO.

• On définit le générateur infinitésimal (A,D(A)) d'un un semi-groupe fortement continu comme l'opérateur non borné où:

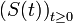
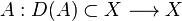
Dans le cas où D(A) = X et la famille d'opérateurs (définie classiquement par sa série) est un semi-groupe fortement continu de générateur infinitésimal A: c'est pourquoi on note parfois abusivement S(t) = e^tA.

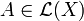
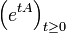
• On dit que le semi-groupe est de contraction si .

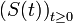
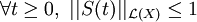
Propriétés des semi-groupes de contraction

• Théorème 1: soit X un espace de Banach, un semi-groupe de contraction sur X et (A,D(A)) son générateur infinitésimal. Alors:

(i) le flot

(ii) et , le flot et vérifie x'(t) = Ax(t)

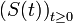
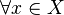
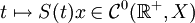
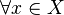
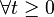
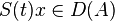
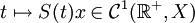
(iii) (A,D(A)) est fermé de domaine dense.

• Théorème 2 (caractérisation des générateurs infinitésimaux): soit un opérateur non borné sur X. On a l'équivalence:

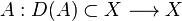
(i) (A,D(A)) est le générateur infinitésimal d'un semi-groupe de contraction

(ii) D(A) est dense et pour toute condition initiale il existe une unique solution de (E).

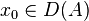
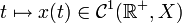
De plus sous cette hypothèse la solution x(t) est à valeurs dans D(A) et vérifie ainsi que (inégalités d'énergie).

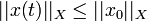
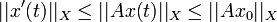
On commence à voir apparaître le lien entre le problème (E) et la notion de semi-groupe. Pour préciser, il faut maintenant introduire la notion d'opérateur dissipatif.

Théorème de Hille-Yosida

Enoncé

• Théorème 3 (Hille-Yosida): soit X un espace de Banach et un opérateur non borné. On a l'équivalence

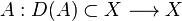
(i) (A,D(A)) est m-dissipatif à domaine dense

(ii) (A,D(A)) est le générateur infinitésimal d'un semi-groupe de contraction

Le point (i) du théorème précédent peut être réécrit en termes de résolvante : (i') (A,D(A)), opérateur fermé à domaine dense, vérifie et .

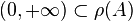
Ainsi sous ces hypothèses et d'après le théorème 2 pour toute condition initiale il existe une unique solution forte dans . Lorsque la condition initiale est prise quelconque dans X on a une solution faible de classe seulement ( et on montre que toute solution faible est limite dans X de solutions fortes).

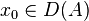
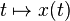
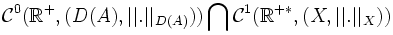
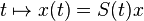
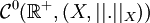
Régularité des solutions

On constate que la régularité de la solution est étroitement liée au choix de la condition initiale en fonction du domaine de A: il est donc naturel de penser qu'en imposant plus de "régularité" à x₀ on obtienne plus de régularité sur les solutions. Plus précisément on pose pour . Alors on a le

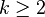
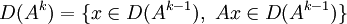
Théorème 4: on peut munir les D(A^k) des normes pour lesquels ce sont des espaces de Banach. De plus si la condition initiale alors la solution est de classe et pour i = 1...k et au sens des topologies précédentes.