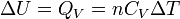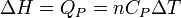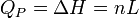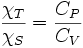Chaleur - Définition
Dans le langage courant, les mots chaleur et température ont souvent un sens équivalent : Quelle chaleur !
La chaleur dans le sens commun a longtemps été confondue avec la notion de température, car à pression constante, c'est une fonction croissante de la température : par exemple tous les corps purs dans l'état solide, liquide ou gazeux ont une capacité calorifique molaire à pression constante CP(T), positive. Dans ces conditions, comme à l'air libre la pression est quasi-constante P ≈ 1,013 25·105 pascals, chauffer un corps engendre une élévation de sa température. Mais cela n'est pas toujours vrai notamment lors d'un changement d'état physique: quand on chauffe de la glace, elle fond à 0°C sous la pression d'une atmosphère, à température constante. Il y a dans ce cas, apport de chaleur sans augmentation de température.
Au XIXe siècle, la chaleur est assimilée à un "fluide": le calorique. Les progrès et les succès de la calorimétrie imposent cette théorie jusqu'à la fin du XIXe siècle. Cette conception est en effet reprise par Sadi Carnot : un moteur thermique ne peut fonctionner que si la chaleur circule d'un corps dont la température est plus élevée vers un corps dont la température est plus froide; raisonnement correspondant à une analogie avec une machine hydraulique qui tire son énergie du passage de l'eau d'un réservoir d'altitude élevée vers un réservoir d'altitude inférieure.
Ce n'est qu'avec l'avènement de la thermodynamique statistique, que la chaleur sera définie comme un transfert de l'agitation thermique des particules au niveau microscopique. Un système dont les particules sont statistiquement plus agitées présentera une température d'équilibre, définie à l'échelle macroscopique, plus élevée. La température est donc une grandeur macroscopique qui est le reflet statistique des énergies cinétiques des particules à l'échelle microscopique. Au cours de chocs aléatoires, les particules les plus agitées transmettent leur énergies cinétiques aux particules les moins agitées. Le bilan de ces transferts d'énergies cinétiques microscopiques correspond à la chaleur échangée entre des systèmes constitués de particules dont l'agitation thermique moyenne est différente.
La température est donc une fonction d'état intensive d'un système thermodynamique définie exclusivement à l'échelle macroscopique. En revanche, la chaleur est un transfert d'agitation thermique qui par nature est désordonné. La chaleur n'est pas une fonction d'état mais une grandeur dépendant de la nature de la transformation mise en jeu.
De plus, il est clair que le transfert ne peut se faire que dans le sens des particules statistiquement les plus agitées vers les particules statistiquement les moins agitées; c'est à dire que la chaleur ne peut passer que du système le plus chaud vers le système le plus froid. Cette hypothèse est confirmée par le second principe de la thermodynamique qui introduit la fonction d'état entropie.
Chaleur et thermodynamique
Le premier principe et la chaleur
Le premier principe de la thermodynamique est un principe de conservation de l'énergie. Il introduit la fonction d'état d'équilibre: U énergie interne.
Au cours d'une transformation d'un système thermodynamique fermé, la variation de l'énergie interne U(B) - U(A) est due soit à :
- la réalisation d'un travail macroscopique W(A → B), en général le travail des forces de pression, ∫-pdV.
- la mise en jeu d'un transfert d'énergies microscopiques ou chaleur, Q(A → B), lors de la transformation .
ΔU = U(B) - U(A) = Q + W
On en déduit donc une définition formelle de la chaleur:
Q(A → B) = U(B)- U(A) - W(A → B) Suivant un chemin bien défini allant de A à B
Si l'on insiste sur cette expression définissant le chemin, c'est que l'intégrale curviligne permettant le calcul du travail des forces de pression (∫ -p.dV), n'est pas indépendante du chemin suivi pour aller de A vers B car le travail n'est pas une fonction d'état.
Il s'ensuit également que La chaleur n'est pas une fonction d'état et donc qu'elle dépend du chemin suivi.
Néanmoins dans certaines conditions expérimentales, la chaleur mise en jeu est égale à la variation d'une fonction d'état. C'est le cas pour une transformation d'un système fermé, effectuée soit à volume constant: ΔU = QV ( voir énergie interne), soit à pression constante: ΔH = QP ( voir enthalpie). Cette propriété est mise à profit dans la calorimétrie effectuée dans un calorimètre fonctionnant soit à pression constante soit à volume constant dans le cas d'une bombe calorimétrique.
Le second principe et la chaleur
Le second principe de la thermodynamique est un principe d'évolution. Il introduit la fonction d'état entropie qui est une mesure du désordre de la matière. Toute transformation réelle spontanée doit accroître le désordre global et se traduire donc par un phénomène de création d'entropie. La fonction entropie est définie à l'échelle macroscopique de telle sorte que sa variation au cours de la transformation d'un système, correspond au rapport de la quantité de chaleur échangée avec le milieu extérieur sur la température du système:
dS = δQrév / T (l'égalité suppose ici que la transformation est réversible: voir le second principe ).
d'où : δQrév = T.dS
Et pour une transformation finie à T constante, allant d'un état(A) à un état(B) d'équilibre:
Qrév = T.ΔS = T.(SB - SA)
La chaleur est donc associée à la notion d'entropie. Plus il y a création d'entropie, plus la transformation est irréversible et plus le travail utile récupéré sera faible ( voir entropie). C'est ce qui justifie le qualificatif donné à la chaleur d'être une forme dégradée de l'énergie ( voir Travail et chaleur).
Calcul de la quantité de chaleur mise en jeu lors d'une transformation affectant un corps pur
Les grandeurs thermodynamiques d'une quantité déterminée de corps pur ( n constant ) ne dépendent que de deux variables indépendantes.
Deux fonctions d'état introduites par le premier principe sont reliées à la chaleur sous certaines contraintes: V=cte ou P=cte.
- À volume constant on choisit la fonction d'état énergie interne.
Fonction d'état énergie interne: U(T,V)
Sa différentielle est égale à:
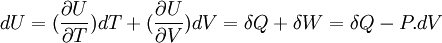
Si V = cte
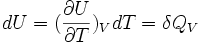
la grandeur
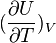
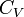
La chaleur mise en jeu pour une mole est donc égale à:
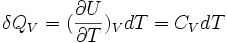
Pour n moles
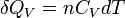
Enfin pour une transformation isochore allant de l'état A défini par TA à un état B défini par TB
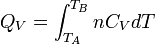
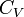
d'où:
|
|
- À pression constante on choisit la fonction d'état enthalpie.
Fonction d'état enthalpie: H(T,P)
Sa différentielle est égale:
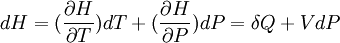
Si P = cte
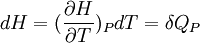
la grandeur
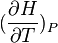
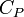
La chaleur mise en jeu pour une mole est donc égale à:
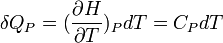
Pour n moles
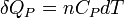
Enfin pour une transformation isobare allant de l'état A défini par TA à un état B défini par TB
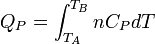
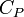
d'où:
|
|
- Cas du changement d'état physique.
Généralement on considère le changement d'état physique effectué à l'air libre c'est à dire à pression constante (pression atmosphérique). Tout le monde sait que la glace fond à 0°C sous la pression atmosphérique et tant qu'il y a coexistence de la glace et de l'eau liquide, la température reste constante. Le changement d'état d'un corps pur s'effectue donc à P = Cte et T = Cte. La chaleur mise en jeu correspond donc à une variation d'enthalpie: ΔH puisque la pression est constante. On l'appelle encore chaleur latente molaire de changement d'état: L.
|
|
Pour en savoir plus ( rédaction à revoir )
L'expression infinitésimale du premier principe pour deux états voisins est :
- Soit U(V,T) l'expression analytique de l'énergie interne U, alors sa différentielle est définie par :
- dU = a·dV + b·dT.
Notons qu'il y a un abus d'écriture, usuel en physique ; on devrait écrire, comme en mathématiques
- U = ƒ(V,T) = g(P,T) = h(V,S) = …
- avec V le volume, T la température, P la pression, S l'entropie…
puisqu'en effet l'état considéré est fixé par deux paramètres, choisis arbitrairement parmi tous les paramètres ; la fonction (au sens mathématique) est donc différente selon la paire de paramètres considérée.
Par définition, b s'appelle la capacité calorifique à volume constant et est notée CV.
Pour une transformation quasi-statique (c'est-à-dire qui évolue suffisamment lentement pour que pression P et température T soient à chaque fois bien définies dans tout le récipient), le travail des forces de pression est
- δ W = - P·dV.
Il en résulte que :
- δ Q = CV·dT + (a + P)·dV
le coefficient (a + P) s'appelle coefficient de chaleur latente de dilatation et est noté ?, égal d'après la formule de Clapeyron à
- ? = P·β·T (cf. Formules de thermodynamique).
β étant l'augmentation relative de pression isochore.
La forme différentielle δ Q s'écrit donc :
- δ Q = CV·dT + P·β·T·dV
Pour un gaz parfait, β·T vaut 1, donc le deuxième terme n'est pas négligeable du tout. Et il est capital pour bien quantifier toute la thermodynamique. On va même le rendre intuitif, pour contrer un raisonnement " faux-conceptuellement " (" chauffer c'est échauffer " est faux) par une intuition éduquée :
- Nous savons tous que si on détend un gaz, très vite, il se refroidit, et a contrario si on comprime un gaz très vite, il se réchauffe (voir Compression et détente adiabatique).
Expliquons-nous sur le terme " très vite " : on veut seulement dire par là que les parois n'auront pas le temps de transmettre de chaleur, la transformation sera adiabatique (on verra plus tard réversible ou non : cf Irréversibilité). Autrement dit, selon le premier principe, il n'y a eu aucune corrélation entre la fluctuation de la force et la fluctuation du mouvement produit, ou en tout cas, elle est négligeable. Alors,
- δ Q = 0
et la relation précédente interprète quantitativement le phénomène : quand le piston s'est détendu, il a fourni du travail, de l'énergie interne a été perdue et la température a décrû. Chacun le sait, une détente adiabatique produit une chute de température dans un gaz, et a contrario, si on bouche un corps de pompe à vélo et qu'on donne un coup de compression large, la température du gaz augmente, puisque, quelques instants plus tard, on ressent une élévation de température de la paroi de la pompe :
- CV·dT = -P·dV·β·T
qui est la relation quantitative énoncée clairement par Clapeyron.
Autre formulation
On peut aussi introduire la fonction d'état enthalpie notée H
- U + PV = H
- dH = CP·dT + V·(1-α·T)·dP
CP étant la capacité thermique à pression constante, comme nous l'indique la deuxième formule de Clapeyron. On en déduit par un calcul analogue au précédent :
- δ Q = CP·dT - V·α·T·dP.
Là encore, nous avions l'intuition de l'existence de ce coefficient : si on détend la pompe par abaissement de pression, et que nous voulons que la température reste constante, nous avons évidemment bien l'intuition qu'il va falloir chauffer le gaz : il faudra qu'il y ait une corrélation entre la fluctuation de pression et la fluctuation de son effet la variation de volume. La relation de Clapeyron indique très quantitativement laquelle :
- δ Q = - V·α·T·dP
Comme quasiment tous les corps se dilatent, c'est bien cette intuition que nous avions, mais nous n'arrivions pas à la formuler. Rien d'étonnant à cela : pas moins de 150 ans ont été nécessaires depuis l'invention de la machine à vapeur par Papin (collaborant avec Huygens), pour que l'ingénieur Clapeyron élabore ces formules.
Mais voici maintenant un élément de réflexion :
- il existe des corps purs pour lesquels la dilatation est négative : l'eau entre 0°C et 4°C
nous l'expliquerons plus tard (cf. Entropie de l'eau et Glace, ceci est dû au réarrangement des molécules sous l'effet des forces de Van der Waals). Cela est contre-intuitif, mais c'est une constation bien banale : l'eau à 4°C étant plus dense, se trouve au fond des lacs (hormis toute considération de salinité). Et néanmoins, la formule fonctionne : dans ce cas, une baisse de pression exigera d'ôter de la chaleur, sinon l'eau s'échaufferait ! Ceci dit, l'effet est faible car la dilatation de l'eau (négative certes) est très petite en module.
Coefficients calorimétriques
On voit donc qu'il y a bien deux sortes de transferts de chaleur. Il y a corrélation entre la fluctuation de la force et la fluctuation de sa conséquence, le déplacement du piston de deux façons :
- l'une effective : elle augmentera effectivement la température,
- l'autre est latente : elle ne produit aucune agitation thermique supplémentaire, la température reste constante. Bien au contraire, elle a été nécessaire pour que la température ne change pas alors que le volume augmentait (resp. que la pression diminuait) et cela est aussi bien naturel en somme : quand les molécules rebondissent sur une raquette-piston en déplacement arrière, le rebond donne une vitesse affaiblie : si l'on veut que l'agitation thermique moyenne, qui est la température (cf Température et Théorie cinétique des gaz), reste la même, il faut cette corrélation positive liée au coefficient de dilatation. Il faut qu'il y ait transfert de chaleur latente (quantifié par Clapeyron).
Résumons et généralisons :
- δQ = CP·dT - V·(α·T)·dP
- δQ = CV·dT + P·(β·T)·dV
La température n'étant pas un paramètre plus privilégié que les autres, on peut aussi écrire
- δQ = λ·dV + μ·dP
Avec des relations entre ces coefficients :
- La relation de Mayer : CP - CV = -P·V·T·β·α
-
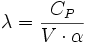
-
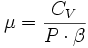
- La relation de Reech :
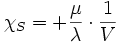
soit compte-tenu des deux précédentes et de α = β·P·χT :