Théorème de Krein-Milman - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le théorème de Krein-Milman est un théorème, démontré par Mark Krein et David Milman en 1940, qui généralise à certains espaces vectoriels topologiques un résultat géométrique portant sur les ensembles convexes énoncé par Hermann Minkowski en dimension finie (et souvent improprement dénommé lui-même « Théorème de Krein-Milman »).
Une forme particulièrement simplifiée du théorème s'énonce : tout polygone convexe est l'enveloppe convexe de l'ensemble de ses sommets. Cela est vrai aussi d'un polytope convexe.
La notion de « point extrémal »
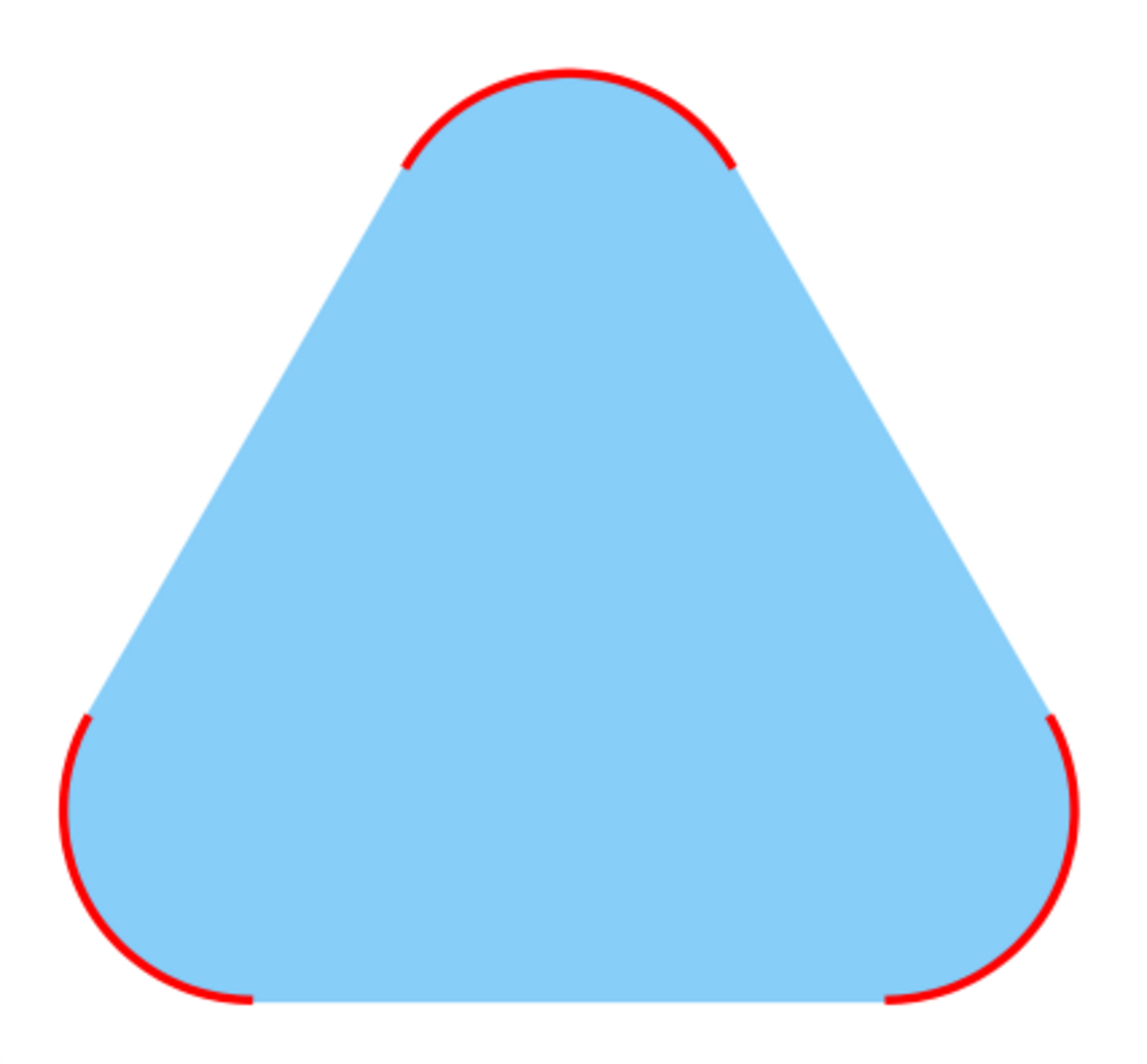
Soit C un convexe et c un point de C. On dit que c est un point extrémal de C lorsque
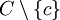
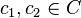
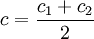
La généralisation en dimension infinie
Théorème — Tout convexe compact d'un espace localement convexe séparé est l'adhérence de l'enveloppe convexe de l'ensemble de ses points extrémaux.
L'énoncé en dimension finie
Théorème — Tout convexe compact d'un espace affine de dimension finie est enveloppe convexe de l'ensemble de ses points extrémaux.
La démonstration n'est pas très longue, l'outil essentiel étant le théorème d'existence d'un hyperplan d'appui en tout point de la frontière d'un convexe.
La démonstration est une récurrence sur la dimension du convexe. Le résultat est évident pour un singleton ; supposons désormais le résultat vrai pour tous les convexes de dimension strictement inférieure à un entier fixé k, et soit C un convexe de dimension k.
Quitte à remplacer l'espace ambiant par l'enveloppe affine de C, on peut supposer que c'est un espace affine dont la dimension est également k.
Prenons maintenant un point m de C et montrons qu'il est dans l'enveloppe convexe des points extrémaux. Pour ce faire, on trace une droite D passant par m. L'ensemble
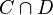
![m\in [a,b]](https://static.techno-science.net/illustration/Definitions/autres/9/9e6aaa2e15c536a74a51596181e6ffb8_a884e4d9c9e94d0e9d0f5895c93d118d.png)
Maintenant a comme b sont adhérents au complémentaire de C, ce sont donc des points frontières de ce convexe. Il existe donc des hyperplans d'appui Ha et Hb en ces points. Introduisons les convexes
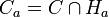
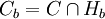
On remarque alors que tout point extrémal de Ca (rep. Cb) est encore un point extrémal de C. Soit en effet c un tel point extrémal de Ca, puis x et y deux points de
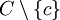
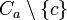
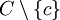
Par ailleurs, comme Ha et Hb sont de dimension k − 1, les deux convexes Ca et Cb sont de dimension strictement inférieure à k. On peut donc leur appliquer l'hypothèse de récurrence. Ceci montre que a (resp. b) est combinaison linéaire de points extrémaux de Ca (resp. Cb), donc de points extrémaux de C. Tant a que b appartient donc à l'enveloppe convexe de ces points extrémaux, puis à son tour m puisqu'il est sur le segment [a,b].

















































