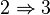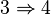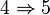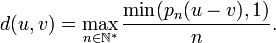Espace localement convexe - Définition
La liste des auteurs de cet article est disponible ici.
Définition
Un espace vectoriel topologique E est dit localement convexe s'il vérifie l'une des deux propriétés équivalentes suivantes :
- la topologie de E peut être définie par une famille de semi-normes ;
- le vecteur nul possède une base de voisinages formée de convexes.
Dans ce cas, la famille de semi-normes peut toujours être choisie filtrante.
- (1)
- En effet toute semi-norme sur E est une fonction convexe et donc pour tout R>0 l'ensemble des x de E vérifiant p(x)<R est convexe.
- (2)
- Soient T la topologie de E, supposée vérifier (2), et T' celle, moins fine, définie par la famille de toutes les semi-normes sur E continues pour T.
- Il s'agit de prouver qu'inversement,
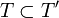
- Or pour un tel V, par continuité de l'application
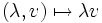
- | λ | < α et
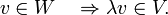
- V contient alors l'ensemble Ω défini par
-
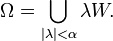
- De plus, Ω est voisinage de 0 (donc absorbant), convexe, et équilibré. Sa jauge est donc une semi-norme continue sur E, dont la boule de centre 0 et de rayon 1/2 est par conséquent un T' -voisinage de 0. Or cette boule est incluse dans Ω, donc dans V.
Continuité d'une fonction
Soient
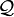
Par exemple (en prenant
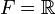
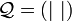
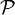
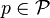
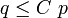
Proposition — Une application linéaire
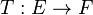
 .
.
Critère de séparation
Théorème — Pour qu'un espace localement convexe E défini par une famille
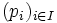
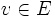
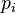
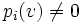
En effet, un espace vectoriel topologique est séparé ssi l'intersection des voisinages de 0 est réduite au singleton {0}, autrement dit ssi pour tout vecteur v non nul, il existe un voisinage de 0 ne contenant pas v.
Espace de Fréchet
Un espace de Fréchet est un espace localement convexe qui est à la fois métrisable et complet au sens des espaces uniformes, ou plus simplement : un espace localement convexe complètement métrisable (c'est-à-dire dont la topologie est induite par une distance complète).
Métrisabilité
Théorème — Soit E un espace localement convexe séparé, dont la topologie est définie par une famille
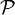
- E est métrisable.
- Tout point de E possède une base dénombrable de voisinages.
- La topologie de E peut être définie par une sous-famille dénombrable
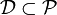
- La topologie de E peut être définie par une famille dénombrable filtrante de semi-normes.
- La topologie de E peut être définie par une distance invariante par translation.
On a clairement
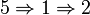
Soit
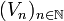
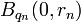
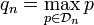
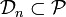
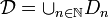
Soit
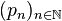
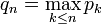
Soit une suite filtrante de semi-normes définissant la topologie de E ; posons pour tous
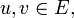
(C'est bien un max : le sup est atteint car la suite est positive et tend vers 0.) Les premier et troisième axiomes d'une distance (symétrie et inégalité triangulaire) sont clairement vérifiés, autrement dit d est un écart. Le deuxième (séparation) résultera du fait que d définit la topologie de E, qui est supposée séparée.
L'invariance par translation de cet écart est également immédiat (
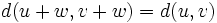
Il reste à montrer que la topologie définie par cet écart est identique à celle définie par la suite de semi-normes. Comme d est invariant par translation, il suffit de montrer que toute d-boule (ouverte) de centre 0 et de rayon positif contient une pn-boule de centre 0 et de rayon positif, et réciproquement. Autrement dit :
-
- Démontrons (i). Soit
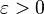
- Démontrons (i). Soit
Pour que
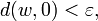
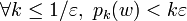
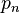
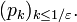
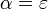
-
- Démontrons (ii). Soit encore ε > 0, et soit
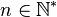
- Démontrons (ii). Soit encore ε > 0, et soit
Pour que
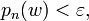
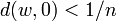
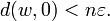
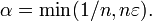
Remarquons qu'un espace vectoriel normé est un espace localement convexe métrisable (topologie définie par une seule semi-norme : la norme). Cependant la réciproque n'est pas vraie car si d est la distance définie ci-dessus, d(0,v) n'est en général pas une norme sur E.
 .
. .
.