Théorie d'Iwasawa - Définition

Introduction

La théorie d'Iwasawa peut être vue comme une tentative d'étendre les résultats arithmétiques classiques sur les corps de nombres (extensions finies du corps des rationnels) à des extensions infinies de , par des procédés de passage à la limite des extensions finies vers les extensions infinies.

Généralités

Les objets de base de la théorie d'Iwasawa sont les -extensions ; c'est-à-dire des extensions galoisiennes dont le groupe de Galois est le groupe profini , pour p un nombre premier fixé. Par la correspondance de Galois, la donnée d'une -extension est équivalente à celle d'une tour d'extensions telle que chaque K_n est galoisienne sur K de groupe de Galois .

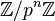
• Pour chaque corps de nombres, une -extension particulière peut-être construite par adjonction de racines p-ièmes de l'unité : la -extension cyclotomique.
• Sous la conjecture de Leopoldt, un corps de nombres admet r₂ + 1 -extensions linéairement indépendantes, où r₂ est le nombre de couples de plongements complexes conjugués du corps considéré ; ce qui peut encore s'énoncer en disant que le compositum de toutes ces extensions a pour groupe de Galois .

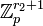
Développements

Le développement des idées d'Iwasawa peut se faire selon plusieurs axes :

• on considère le comportement le long des étages d'une -extension d'autres objets que le groupe de classes, notamment du groupe de Mordell-Weil d'une courbe elliptique. On parle de théorie d'Iwasawa des courbes elliptiques.
• on considère le comportement des objets arithmétiques non plus le long d'une -extension, mais dans des extensions infinies ayant d'autres groupes de Galois : par exemple , ou plus généralement un groupe analytique p-adique. Se développe ainsi une théorie d'Iwasawa non commutative, notamment sous l'impulsion de John Coates.

Théorème fondamental

Le théorème fondateur de la théorie, dû à Iwasawa, porte sur le comportement du groupe des classes le long d'une -extension. Soit un nombre premier, un corps de nombres, et une -extension de . Pour chaque , on s'intéresse au cardinal du -Sylow du groupe des classes de  ; notons le . Alors, il existe des entiers , (positifs), (de signe quelconque), tels que pour assez grand, on ait :

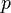
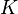
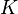
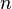
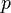
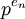
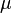
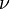
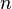
Idée de la démonstration

Notons A(K_n) le p-Sylow du groupe des classes du corps K_n. Par la théorie du corps de classes, il existe une extension L_n de K_n tel que  : L_n est la p-extension abélienne non ramifiée maximale de K_n. L'union des corps L_n fournit alors un corps L, qui est la pro-p- extension abélienne non ramifiée maximale de .

On considère alors le groupe de Galois  :

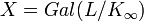
• X est la limite projective des groupes Gal(L_n / K_n), qui apparaissent comme des quotients de X.
• X en tant que pro-p-groupe abélien a une structure naturelle de -module.
• Par ailleurs, le groupe de Galois de l'extension cyclotomique agit sur X, dont on peut montrer qu'il est ainsi muni d'une structure de -module, c'est-à-dire de module d'Iwasawa.

L'investigation de la structure des modules d'Iwasawa relève de l'algèbre linéaire. Connaissant leur classification à pseudo-isomorphisme près, et ayant calculé par quel sous-groupe on quotiente X pour obtenir Gal(L_n / K_n), on peut en déduire l'estimation asymptotique du cardinal de ces groupes, qui founrit la formule annoncée sur A(Kⁿ).

Quelques résultats et conjectures

• L'invariant μ est nul pour la -extension cyclotomique au-dessus d'une extension abélienne de (théorème de Ferrero-Washington). Des exemples sont connus d'autres extensions où il n'est pas nul.
• L'invariant λ est connu par exemple pour les corps quadratiques imaginaires, par la formule de Kida. Il est conjecturé qu'il est nul pour les corps totalement réels, c'est la conjecture de Greenberg.
• La structure de module d'Iwasawa du groupe est relié dans certains cas à certaines fonctions L p-adiques, par la conjecture principale en théorie d'Iwasawa, devenue théorème de Mazur-Wiles.