Triangulation de Delaunay - Définition
La liste des auteurs de cet article est disponible ici.
Applications
L'arbre euclidien couvrant de poids minimum d'un ensemble de points est un sous-ensemble de la triangulation de Delaunay de ces mêmes points. Ce résultat permet de calculer efficacement cet arbre.
Pour modéliser un terrain ou d'autres objets à partir d'un ensemble de points donnés, la triangulation de Delaunay fournit un bon ensemble de triangles qui pourront ensuite être utilisés comme polygones dans le modèle.
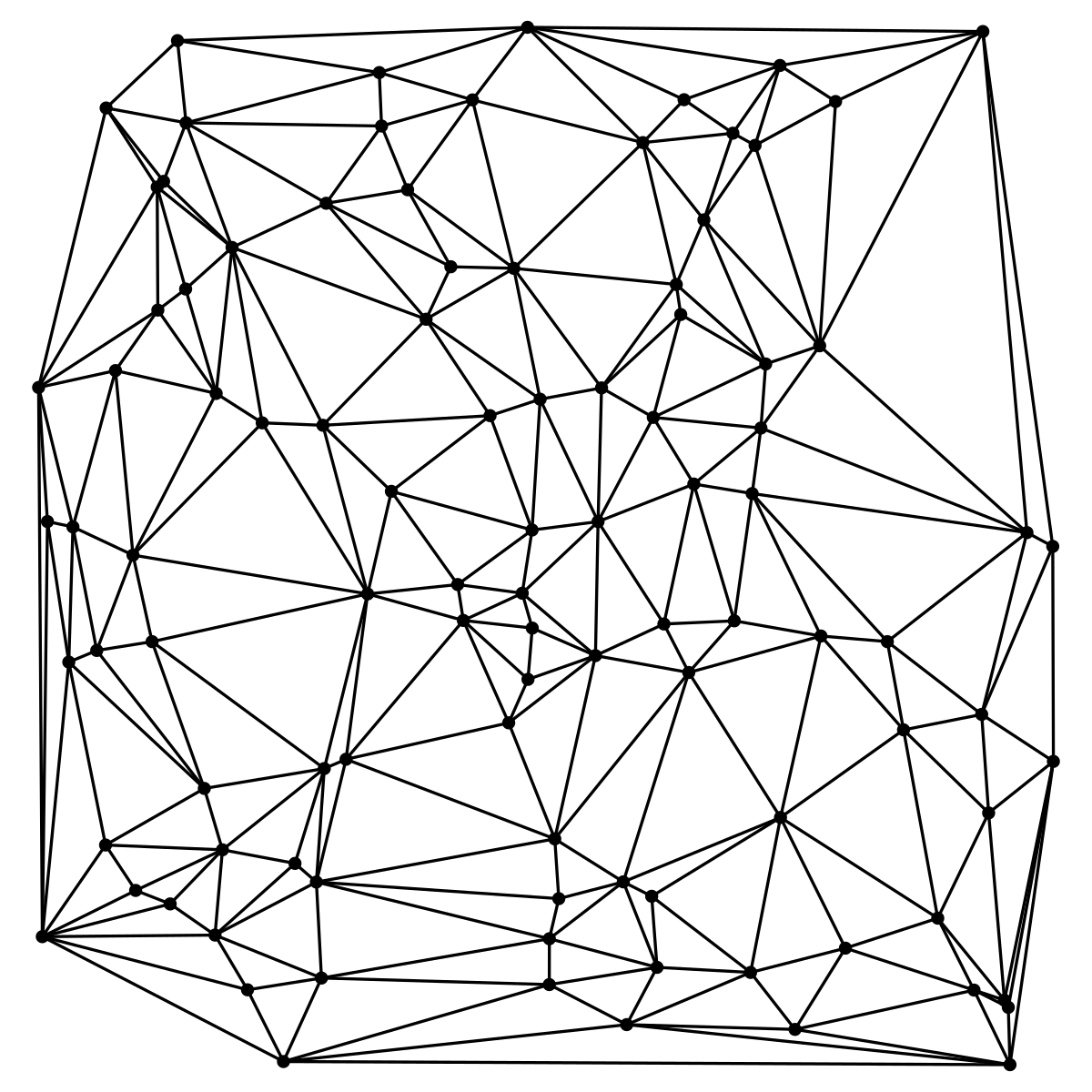
Les triangulations de Delaunay sont souvent utilisées pour construire les mailles de la méthode des éléments finis à cause de la garantie sur les angles et grâce à la vitesse des algorithmes. Typiquement, le domaine dont on veut construire les mailles est décrit comme un gros complexe simplicial. Pour que le maillage soit stable numériquement, il faut qu'il soit raffiné, par exemple en utilisant l'algorithme de Ruppert. Jonathan Shewchuk a publié une bibliothèque libre sur les triangles.

















































