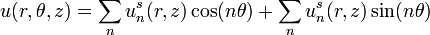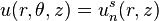Méthode des éléments finis - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
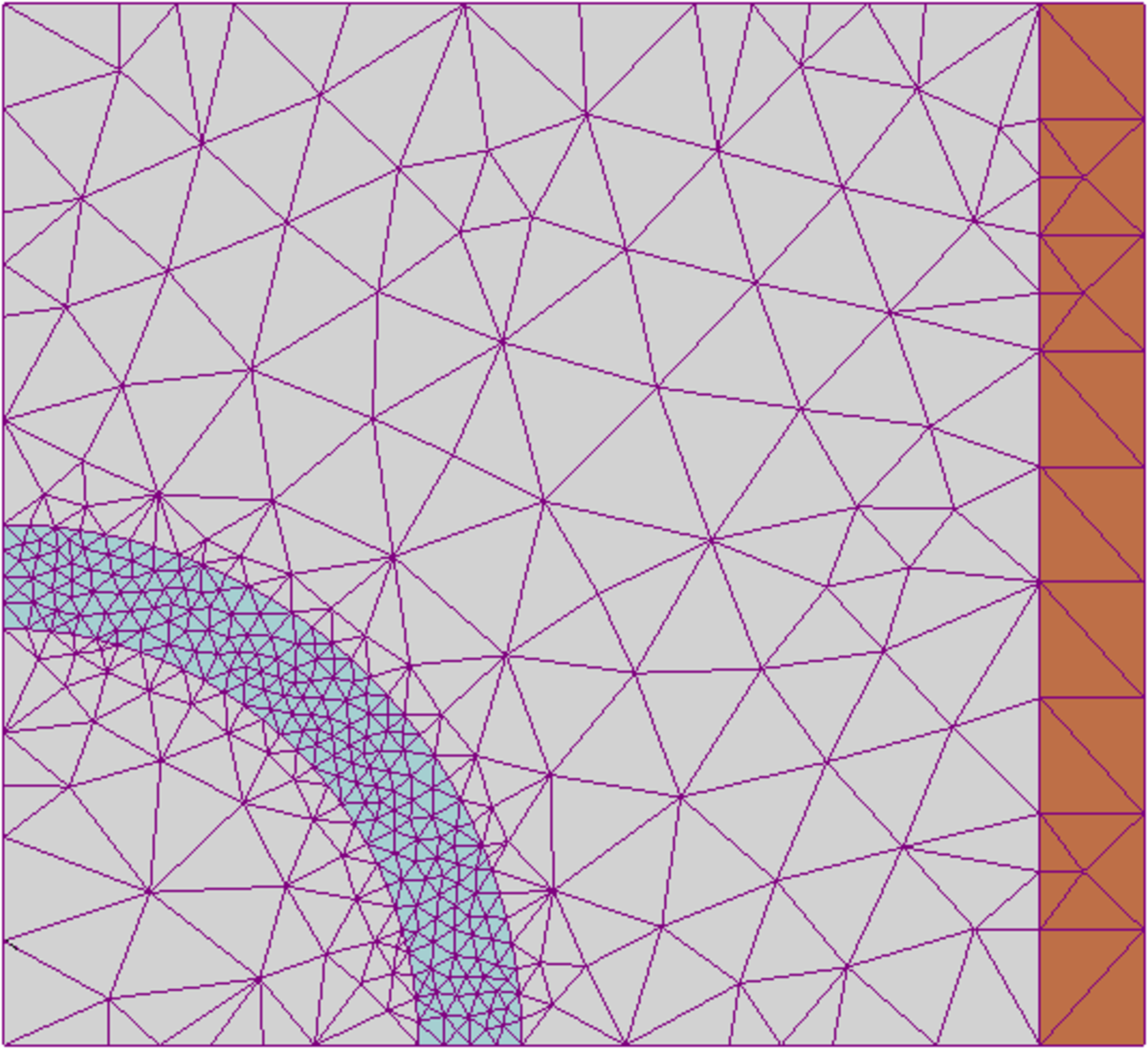
En analyse numérique, la méthode des éléments finis est utilisée pour résoudre numériquement des équations aux dérivées partielles. Celles-ci peuvent par exemple représenter analytiquement le comportement dynamique de certains systèmes physiques (mécaniques, thermodynamiques, acoustiques, etc.).
Concrètement, cela permet par exemple de calculer numériquement le comportement d'objets même très complexes, à condition qu'ils soient continus et décrits par une équation aux dérivées partielles linéaire : mouvement d'une corde secouée par l'un de ses bouts, comportement d'un fluide arrivant à grande vitesse sur un obstacle, déformation d'une structure métallique, etc.
Introduction
La méthode des éléments finis fait partie des outils de mathématiques appliquées. Il s'agit de mettre en place, à l'aide des principes hérités de la formulation variationnelle ou formulation faible, un algorithme discret mathématique permettant de rechercher une solution approchée d’une équation aux dérivées partielles (ou EDP) sur un domaine compact avec conditions aux bords et/ou dans l'intérieur du compact. On parle couramment de conditions de type Dirichlet (valeurs aux bords) ou Neumann (gradients aux bords) ou de Robin (relation gradient/valeurs sur le bord).
Il s'agit donc avant tout de la résolution approchée d'un problème, où, grâce à la formulation variationnelle, les solutions du problème vérifient des conditions d'existence plus faibles que celles des solutions du problème de départ et où une discrétisation permet de trouver une solution approchée. Comme de nombreuses autres méthodes numériques, outre l'algorithme de résolution en soi, se posent les questions de qualité de la discrétisation :
- existence de solutions,
- unicité de la solution,
- stabilité,
- convergence,
- et bien sûr : mesure d'erreur entre une solution discrète et une solution unique du problème initial.
La partie 2 va présenter le cadre général de la méthode des éléments finis, ainsi que le cas pratique le plus courant considérant des équations aux dérivées partielles linéaires dont on cherche une approximation par des fonctions affines.
La présentation en partie 3 est essentiellement physique, notamment mécanique. Elle ne doit être considérée que comme une présentation des éléments constitutifs de la modélisation discrète utilisée en résistance des matériaux via la méthode des éléments finis. C'est une approche tout à fait valide, un bon exemple pédagogique. Elle apporte un biais certain quant à une approche plus générale, du fait notamment de la linéarité supposée des matériaux.
Exemples issus de problèmes physiques
Historique
- Analyse des structures née vers 1850
- RDM (Résistance des matériaux) ⇒ calculs « manuels »
Maxwell, Castigliano, Mohr - Concept d'éléments finis né vers 1940
Newmark, Hrenikoff, Mc Henry, Courant - Développement réel depuis 1960
Calcul numérique sur ordinateur
- RDM (Résistance des matériaux) ⇒ calculs « manuels »
Domaines d'application
- Calcul de structures, étude des contacts, électricité, électromagnétisme, hydraulique, aérodynamique, finance, ingénierie biomédicale, ...
Principe
- Le milieu continu est « idéalisé » par la subdivision en un nombre fini d'éléments dont le comportement est représenté par un nombre finis de paramètres.
- La résolution du problème global, obtenu par assemblage des éléments, suit les règles qui régissent les structures discrètes.
Les difficultés
- D'ordre théorique : formulation des éléments
- D'ordre pratique :
- Discrétisation du milieu continu (maillage)
- Qualité des résultats (convergence de la méthode)
Exemple de problème discret : un réseau électrique
- Équation locale du composant e :
-
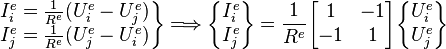
- soit
![\left\{ I^e \right\} = \left[ K^e \right] \left\{ U^e \right\} \,](https://static.techno-science.net/illustration/Definitions/autres/3/3904acf5a7a456a99343ddf2f039ebd3_68fe96d2c5545d68e6f500f4a8c2ea1a.png)
- soit
-
- On écrit :
- La continuité des potentiels en chaque connexion
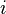
- L'équilibre des courants à chaque connexion
- L'adjonction des courants externes
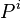
- La continuité des potentiels en chaque connexion
- On obtient l'équation globale du système assemblé :
-
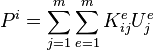
- soit
![\left\{ P \right\} = \left[ K \right] \left\{ U \right\} \,](https://static.techno-science.net/illustration/Definitions/autres/a/ac36981ea28fe5fd5742e34f5072df01_8fb1d0fc32b1e8a742dc717f4d18c2d4.png)
- soit
-
Définition d'un élément fini
- En calcul de structures, un élément fini est caractérisé par deux matrices :
- La matrice de raideur
![\left[ K \right] \,](https://static.techno-science.net/illustration/Definitions/autres/1/16b9ccf8affc2509a6735cfc6a7d2209_3a792a1dcf4a302b636742bf96b0cb03.png)
- La matrice de masse
![\left[ M \right] \,](https://static.techno-science.net/illustration/Definitions/autres/9/9ec470f14f305ee50ab76fefc600a3aa_c45b71ddf338601da8f660a3ba86f1e7.png)
- La matrice de raideur
Formulation d'un élément fini
Définitions et notations
- Déplacement :
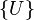
- C'est un vecteur dont chaque composante est également appelée degré de liberté
- 3 ddl de translation :
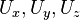
- 3 ddl de rotation :
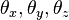
- 3 ddl de translation :
- Déformation : (voir Tenseur des déformations)
![\left[ \epsilon \right] \,](https://static.techno-science.net/illustration/Definitions/autres/7/70fa3bbf7e8c175572d12001dd560632_915a2924657f554340ea1bae161b7f69.png)
- C'est le rapport de l'allongement à la longueur initiale.
En petites déformations, on a
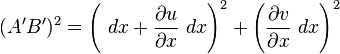
Comme
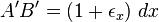
On néglige les termes d'ordre 2 :
Remarque :

- Contrainte : (voir Tenseur des contraintes)
![\left[ \sigma \right] \,](https://static.techno-science.net/illustration/Definitions/autres/2/293f43c1c757bf10b4725d9a7df000be_f92ddff677ba42f0724f036d59b4e72f.png)
-
- Elle représente les efforts internes qui s'appliquent dans la structure.
-
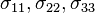
-
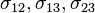
- Une contrainte est homogène à une pression (N/m²)
- Il existe un système de coordonnées dans lequel
![\left[ \sigma \right] \,](https://static.techno-science.net/illustration/Definitions/autres/2/293f43c1c757bf10b4725d9a7df000be_f92ddff677ba42f0724f036d59b4e72f.png)
![\left[ \sigma \right] = \begin{bmatrix}\sigma_X & 0 & 0 \\ 0 & \sigma_Y & 0 \\ 0 & 0 & \sigma_Z\end{bmatrix} \,](https://static.techno-science.net/illustration/Definitions/autres/8/873dc515d9ceaff74e876e55a482af07_f4c5169b4bed7b0d469cf1be4e4e971f.png)
-
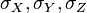
- Elle représente les efforts internes qui s'appliquent dans la structure.
- Relations Contraintes-Déformations : (voir Loi de Hooke) ≡ lois de comportement
-
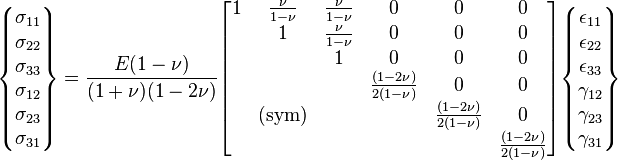
-
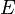
-
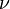
- On utilise parfois le module de cisaillement :
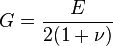
- Pour un matériau isotrope, il n'y a que 2 paramètres indépendants. Il y en a 6 pour un matériau isotrope transverse, 9 pour un matériau orthotrope et 21 pour un matériau anisotrope
- En notation matricielle, on écrit :
![\left\{ \sigma \right\} = \left[D\right]\left\{ \epsilon \right\} \,](https://static.techno-science.net/illustration/Definitions/autres/7/714b6be5752204781d2dc8cd37f4b4d0_2b46196f364de9a62fa3845bd4873531.png)
-
![\left[D\right] \,](https://static.techno-science.net/illustration/Definitions/autres/7/7aa36b83a9ecd06dc5f55ccb4de0b697_02ef4158c37e3c69993bcf260a24c040.png)
-
- Énergie de déformation :
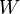
- Travail d'une force :
- C'est le produit de la force par le déplacement de son point d'application :
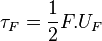
- Moment :
- C'est une force appliquée sur un ddl de type rotation
Équations fondamentales
Équations d'équilibre local :
Relations déformations-déplacements :
-
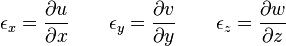
-
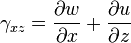
-
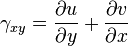
-
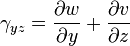
- Symboliquement, on écrit
![\{\epsilon\} = [S]\{U\} \,](https://static.techno-science.net/illustration/Definitions/autres/7/724941f6b0af3275412d58b61e363851_a56fe2d909b8659fc8a698eb7262cb15.png)
- Symboliquement, on écrit
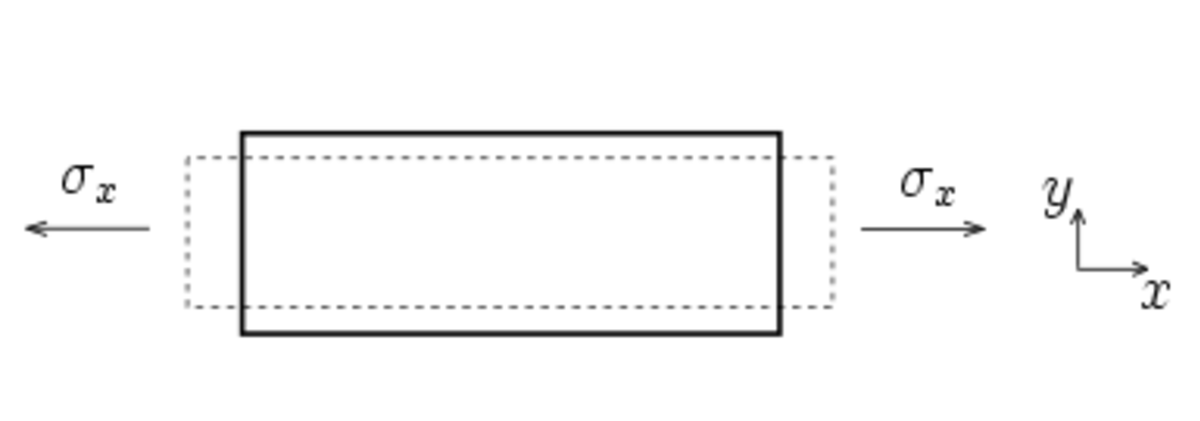
Si on applique au barreau une contrainte
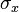
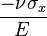
Quelques valeurs usuelles :
- Acier : E = 2,1E11 N/m² = 210 000 MPa
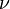
- Aluminium : E = 7E10 N/m² = 70 000 MPa
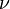
Remarques : On a toujours -1
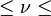
Quand
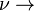
Exemple de formulation : Barre en traction
On suppose que le déplacement en tout point de la barre est donné par un polynôme du 1er degré :
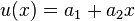
- On a
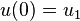
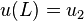
- d'où
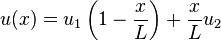
qu'on écrit symboliquement :
![u(x) = [N(x)]\{U\} \,](https://static.techno-science.net/illustration/Definitions/autres/b/bd71f8698ea9d9a67352b60b2703383e_cd73f82e24c7f64dfb7718dd98062450.png)
![\left|\begin{matrix}[N(x)] & = & \left[ \left(1-{x \over L}\right) ; \left({x \over L}\right) \right] \\ \{U\} & = & \begin{Bmatrix}u_1 \\ u_2 \end{Bmatrix} \end{matrix}\right. \,](https://static.techno-science.net/illustration/Definitions/autres/9/9d82fb42917a9b7afe2e08bf192d3458_b4957594b6260ac40a03aad7bc412c60.png)
On en déduit :
D'autre part, on a par définition :
-
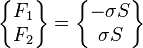
On pose :
On obtient finalement :
Soit une relation du type :
En explicitant :
On voit que la matrice de rigidité se calcule comme le produit de 3 matrices :
-
![[B] \,](https://static.techno-science.net/illustration/Definitions/autres/3/3c20ce1fba7af3dfdcbc27bb67b41df9_5d656acc93797e178ceb0eebf8aaefec.png)
-
![[D] \,](https://static.techno-science.net/illustration/Definitions/autres/7/7e1d66cda0f587d6329839697e00fd3b_7dac4f9d33648a054be315e8510baf55.png)
-
![[A] \,](https://static.techno-science.net/illustration/Definitions/autres/8/8400745d063bd8529152a1cacc6da32b_a02b0f57873cdb1fa833e14a3dc92a3b.png)
Formulation générale (méthode directe)
- La démarche est la suivante :
- On exprime le déplacement
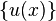
![\{u(x)\} = [N(x)]\{U\}\,](https://static.techno-science.net/illustration/Definitions/autres/a/adb1cb2ad9990a8611845367d5eb6b21_b66502c600d1adcbbd9311ec8bc35cd8.png)
- On exprime les déformations en fonction des déplacements
![\{\epsilon(x)\}=[S]\{u(x)\}\,](https://static.techno-science.net/illustration/Definitions/autres/6/6434b863ed4484c25a91240e5b61ff1e_921fe4ac6b4270644d3e83acc7880b10.png)
- d'où
![\{\epsilon(x)\}=[S]\{N(x)\}\{U\}=[B(x)]\{U\}\,](https://static.techno-science.net/illustration/Definitions/autres/f/f674157ad421fa0719a7c9d2c92bea49_16a1dca4a2440148478d5b1c852e896f.png)
- On écrit la loi de comportement du matériau qui relie les contraintes aux déformations :
![\{\sigma(x)\}=[D]\{\epsilon(x)\}\,](https://static.techno-science.net/illustration/Definitions/autres/0/0bb4f8e11c093b18894c2e7d85f7be04_5461b025c7e4fc74c98bb85b05fda34c.png)
- On écrit que le travail des forces externes appliquées à la structure pour un déplacement virtuel
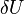
-
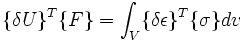
- En explicitant, on a :
-
![\{\delta U\}^T\{F\}=\{\delta U\}^T \left (\int_V [B]^T[D][B] dv \right ) \{U\} \,](https://static.techno-science.net/illustration/Definitions/autres/4/422a7742ac87147eadec59c8ba1d220f_5c38e828d3c9b3f25e9e1cae98e4d059.png)
- Comme cette relation est vraie pour tout déplacement virtuel, on en déduit :
-
![\{F\}=[K]\{U\} \,](https://static.techno-science.net/illustration/Definitions/autres/2/256b1c17205d63549ff12bd58cb6cff2_c8bb1eeb2bd57e2a22df4cf406ef9576.png)
- avec
![[K] \,](https://static.techno-science.net/illustration/Definitions/autres/d/dfd8a53448ecbc9971fbc6f5b3355d12_29d055d676039d5c94dd96bd835c9beb.png)
![[K]=\int_V [B]^T[D][B] dv \,](https://static.techno-science.net/illustration/Definitions/autres/a/a42471892fcd3221043a1d0e68f94d7c_7b12442380db60eace18c1618ee6ff8c.png)
Remarques :
- La relation ci-dessus montre que
![[K] \,](https://static.techno-science.net/illustration/Definitions/autres/d/dfd8a53448ecbc9971fbc6f5b3355d12_29d055d676039d5c94dd96bd835c9beb.png)
- Le terme courant
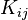
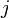
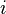
La symétrie de
![[K] \,](https://static.techno-science.net/illustration/Definitions/autres/d/dfd8a53448ecbc9971fbc6f5b3355d12_29d055d676039d5c94dd96bd835c9beb.png)
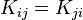
Qu'est-ce qui va différencier les différents types d'éléments finis ?
- Le choix des fonctions N(x)
- La nature de l'opérateur S (reliant déformations et déplacements) qui dépend du type de théorie élastique utilisée :
-
- théorie des poutres
- théorie des plaques
- théorie de la contrainte ou de la déformation plane
- théorie des coques
- théorie des corps de révolution
- théorie de l'élasticité 3D
Remarques :
Nous avons décrit le processus de formulation d'un élément fini dans le cadre de la méthode directe.(dite aussi méthode des déplacements) Il existe d'autres approches :
-
- La méthode des résidus pondérés
- L'application du principe des travaux virtuels ou des puissances virtuelles
- La minimisation de l'énergie potentielle
Toutes ces approches sont équivalentes et aboutissent à la construction de la même matrice de rigidité.
Éléments finis en contraintes
Au lieu de rechercher une solution approchée en déplacement, on peut aussi rechercher la solution approchée en contrainte.
Dans le cas de la mécanique, l'application du principe des puissances virtuelles donne de manière non triviale les théorèmes énergétiques. On peut aboutir au même résultat en quelques lignes en écrivant l'erreur en relation de comportement.
L'approche en contrainte consiste à rechercher dans l'espace des champs de contraintes admissibles celui qui réalise le minimum de l'énergie complémentaire.
Cette approche est plus précise que l'approche en déplacement mais elle est peu développée du fait de la difficulté que l'on a à générer des champs de contraintes de divergence donnée.
Étude des fonctions N(x)
- Dans le cas général de l'élasticité tridimensionnelle, ce sont en fait des fonctions de x, y, z.
- Les fonctions les plus couramment utilisées sont des polynômes.
-
-
- Polynôme de degré 1 : élément linéaire (2 nœuds par arête)
- Polynôme de degré 2 : élément parabolique (3 nœuds par arête)
- Polynôme de degré 3 : élément cubique (4 nœuds par arête)
-
- etc.
- etc.
-
Les fonctions N(x) sont appelées fonctions de forme ou fonctions d'interpolation de l'élément.
Les éléments isoparamétriques
Problème
- Soit on construit
![[K] \,](https://static.techno-science.net/illustration/Definitions/autres/d/dfd8a53448ecbc9971fbc6f5b3355d12_29d055d676039d5c94dd96bd835c9beb.png)
- Soit on utilise des éléments à géométries variables ⇒ il faut reconstruire
![[K] \,](https://static.techno-science.net/illustration/Definitions/autres/d/dfd8a53448ecbc9971fbc6f5b3355d12_29d055d676039d5c94dd96bd835c9beb.png)
D'où l'idée
Pour construire la matrice de raideur d'un élément à géométrie variable, on va utiliser des fonctions d'interpolation pour décrire non seulement le champ de déplacement de l'élément mais également sa géométrie. De plus, on va travailler en coordonnées locales.
Interpolation de la géométrie
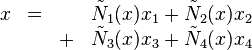
Idem pour les autres coordonnées. |
Coordonnées locales (cas 2D)
Élément isoparamétrique
Un élément est dit isoparamétrique si on prend les mêmes fonctions d'interpolation pour le déplacement et la géométrie.
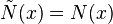
Autres classes d'éléments
Évaluation de K
La forme générale s'écrit :
![[K]=\int_x \int_y \int_z G(x,y,z) dxdydz \,](https://static.techno-science.net/illustration/Definitions/autres/a/a43855af644b1b26766780b5eca47f14_97ddc73a07eafa16110e8e4dd0265abf.png)
On passe en variables locales
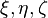
On a
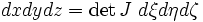
-
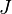
On est alors amené à calculer des intégrales du type :
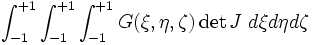
Bénéfice de l'approche
On s'est ramené à un domaine d'intégration simple et invariant pour lequel on peut appliquer les formules de quadrature de gauss :
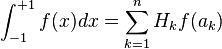
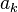
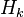
Les
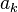
Cas particulier : les éléments axisymétriques
Décomposition en série de Fourier :
L'axisymétrie correspond à la restriction
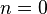
Remarque importante : Pour utiliser ce type d'élément, le problème doit être globalement axisymétrique :
- la géométrie
- les conditions limites
- le chargement
Processus de calcul (cas statique)
- Maillage
- Construction de la matrice de raideur de chaque élément
![[K^e] \,](https://static.techno-science.net/illustration/Definitions/autres/c/c6cc6749b6a172a7cc4531505fbe30dc_10ee7f172628cb262532a3ac29e6ce1d.png)
- Assemblage de la matrice globale
![[K] \,](https://static.techno-science.net/illustration/Definitions/autres/d/dfd8a53448ecbc9971fbc6f5b3355d12_29d055d676039d5c94dd96bd835c9beb.png)
- Construction du vecteur chargement
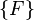
- Élimination de certains ddl (si besoin)
- Résolution :
![\{U\} = [K^{-1}]\{F\} \,](https://static.techno-science.net/illustration/Definitions/autres/d/db9f8dd1d3c028e7ef66c1c63f3912af_402114603191a6d963d5d3ef9aee754b.png)
- Calcul des quantités dérivées de
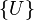
-
-
![\{\epsilon^e\} = [B^e] \{U^e\} \,](https://static.techno-science.net/illustration/Definitions/autres/9/9338268e64521c4580e7784025b0d1ce_41a3f02a9048e684133f12bcbed911ef.png)
-
![\{\sigma^e\} = [D^e] \{\epsilon^e\} \,](https://static.techno-science.net/illustration/Definitions/autres/d/d54dbe873aaf678061477e2a14e53a11_3aab89ca06471a9c9c60662365f2aef0.png)
-
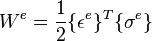
-
- etc.
-
-

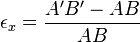
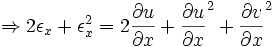
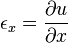
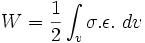
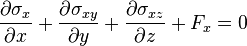
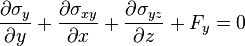
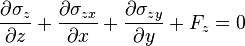
![\epsilon = \left[-{1 \over L} ; {1 \over L} \right]\begin{Bmatrix}u_1 \\ u_2\end{Bmatrix} = [B]\{U\} \,](https://static.techno-science.net/illustration/Definitions/autres/e/e4a26bd4e8d69bb13e6b1b156949ceb8_0864cfbb51979adaa755eb93c234f3e1.png)
![\sigma = E\left[-{1 \over L} ; {1 \over L} \right]\begin{Bmatrix}u_1 \\ u_2\end{Bmatrix} = [D]\epsilon \,](https://static.techno-science.net/illustration/Definitions/autres/2/2d2a7af6387aaf354c01a6053279d304_bfd7587a9b7509b419b905cff4998c9d.png)
![\{F\} = \begin{Bmatrix}F_1 \\ F_2 \end{Bmatrix} = [A]\sigma \qquad \mbox {avec} \qquad \{A\} = S \begin{Bmatrix}-1 \\ 1 \end{Bmatrix} \,](https://static.techno-science.net/illustration/Definitions/autres/1/1d01181c6e890ad31843c10ee38fad9b_3c27d38767d175ca1f9227c5c359a5bd.png)
![\{F\} = [A][D][B]\{U\} \,](https://static.techno-science.net/illustration/Definitions/autres/5/55656625cf793be5a336c3c9fdeecba0_934361378b2c9a34b0c53bfff57e5c61.png)
![\{F\} = [K]\{U\} \qquad \mbox {avec} \qquad [K] = [A][D][B] \,](https://static.techno-science.net/illustration/Definitions/autres/b/b5beef13b34aab89c1c2b00e8afe79a3_4c56d7df97e7227800e4438777ee5ee0.png)
![[K] = {ES \over L} \begin{bmatrix}1 & -1 \\ -1 & 1 \end{bmatrix} \,](https://static.techno-science.net/illustration/Definitions/autres/5/53f32fd25a05dbdc17ff442790a214da_b425057b8a9842b99e0d78efddd259ea.png)