Triangulation de Delaunay - Définition

Algorithmes

Tous les algorithmes pour construire une triangulation de Delaunay reposent sur des opérations rapides permettant de détecter lorsqu'un point est à l'intérieur d'un triangle circonscrit et de structures de données efficaces pour conserver les triangles et les sommets. Dans le plan, une manière de détecter si un point D se trouve dans le cercle circonscrit de A, B et C est d'évaluer le déterminant de la matrice suivante :

En supposant que A, B et C sont placés dans le sens anti-horaire, ce nombre est positif si et seulement si D se trouve dans le cercle circonscrit.

Algorithmes de basculement

Comme mentionné ci-dessus, si un triangle n'est pas de Delaunay, il est possible de basculer l'un de ses côtés. On construit ainsi un algorithme direct : on génère d'abord une triangulation quelconque, puis on bascule les arêtes jusqu'à ce que tous les triangles soient de Delaunay. Cette méthode peut nécessiter O(n²) basculements d'arêtes et ne peut se généraliser en dimension 3 ou supérieure.

Incrémentation

La manière la plus directe de générer efficacement une triangulation de Delaunay est d'ajouter les sommets un par un en recalculant la triangulation des parties du graphe affectées par cet ajout. Lorsqu'un sommet s est ajouté, le triangle contenant s est séparé en trois puis on leur applique l'algorithme de basculement. Fait de manière naïve, cela se fera en temps 0(n) : il faut chercher parmi tous les triangles pour trouver celui qui contient s et tous les triangles vont ensuite potentiellement basculer. Comme il faut faire cela pour chaque sommet, le temps total d'exécution est en O(n²).

Si les sommets sont insérés dans un ordre aléatoire, chaque insertion ne va faire basculer, en moyenne, que O(1) triangles, même si parfois beaucoup plus vont basculer.

Pour améliorer la recherche de la position du point, il est possible de stocker l'historique des partitionnements et des basculements effectués : chaque triangle garde en mémoire un pointeur vers les deux ou trois triangles qui l'ont remplacé. Pour trouver le triangle qui contient s, commencer à un triangle racine, puis suivre les pointeurs jusqu'à arriver à un triangle qui n'a pas été remplacé. En moyenne, cela se fera en temps 0(log n). Ainsi, pour rechercher le triangle conteneur de chaque sommet, cela se fera en temps O(n log n). La technique peut être généralisée à des espaces de dimension quelconque, comme l'ont prouvé Edelsbrunner et Shah, mais la complexité temporelle peut être exponentielle, y compris si la triangulation finale est petite.

Diviser pour régner

Lee et Schachter ont mis au point un algorithme diviser pour régner appliqué à la triangulation en deux dimensions qui a ensuite été amélioré par Guibas et Stolfi puis par Dwyer. Dans cet algorithme, une ligne est récursivement dessinée pour séparer les points en deux ensembles. La triangulation de Delaunay est calculée pour chacun des ensembles puis ils sont fusionnés. Avec quelques astuces, la fusion peut se faire en O(n). Ainsi, le temps total de calcul est en O(n log n).

Une définition visuelle : le basculement

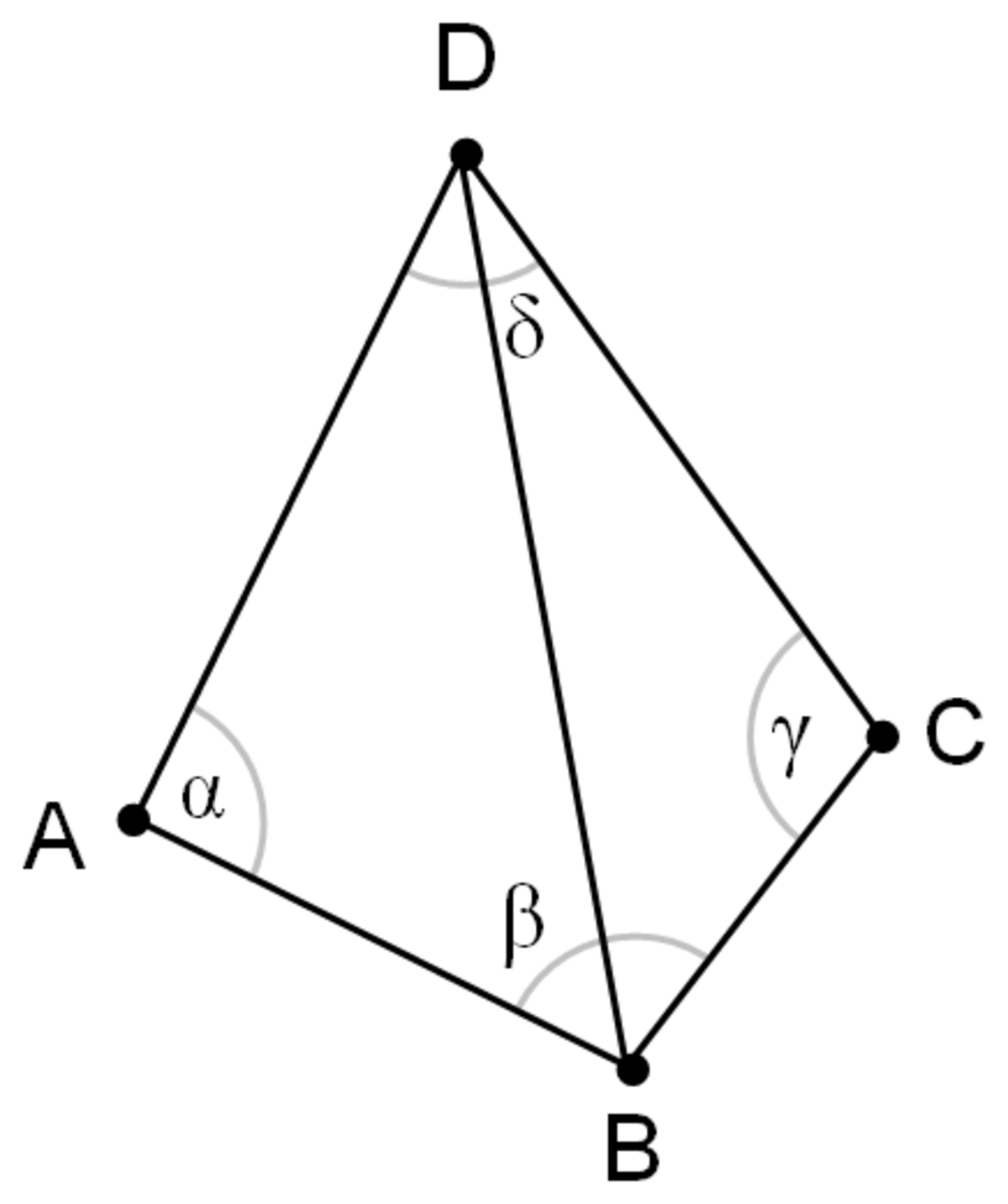
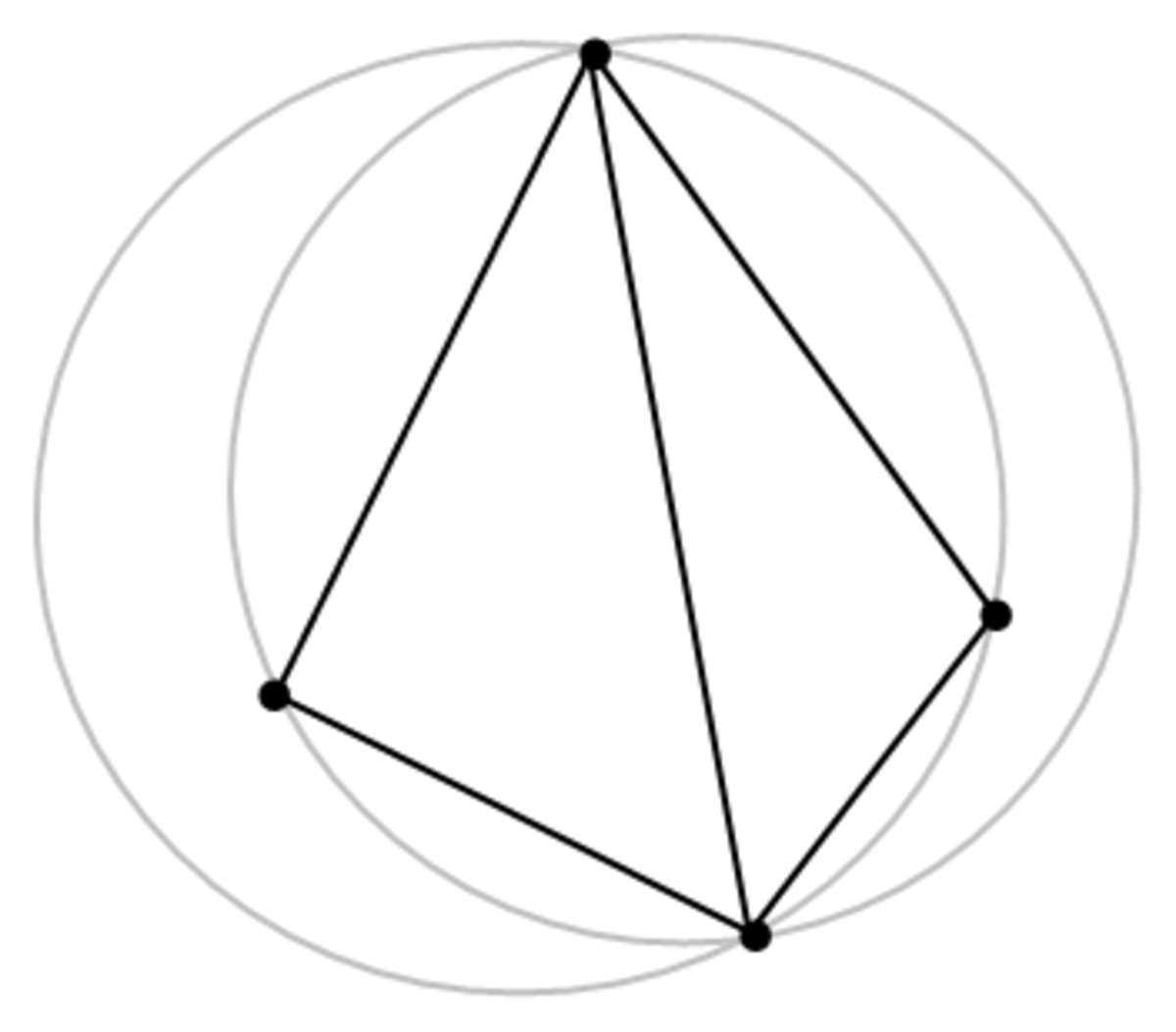
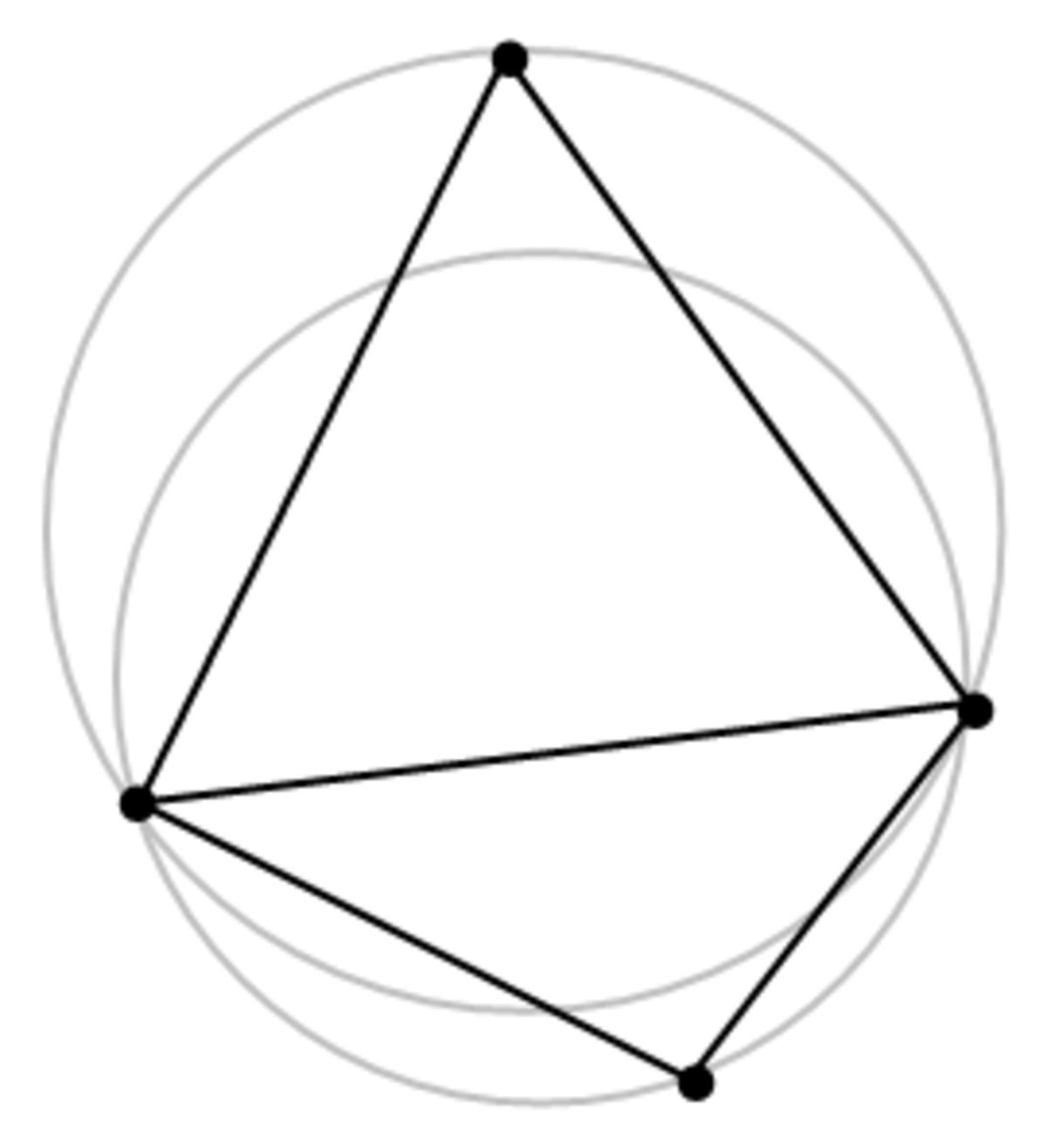
D'après les propriétés précédentes, on peut remarquer qu'avec deux triangles ABD et BCD donnés (voir figure), si la somme des angles α et γ est inférieure ou égale à 180° alors ces triangles respectent la condition de Delaunay.

C'est une propriété importante car elle permet de déterminer une technique de construction. Si deux triangles ne respectent pas la condition de Delaunay, remplacer l'arête commune BD par l'arête commune AC (ce qui constitue le basculement), générant ainsi deux triangles qui respectent la condition de Delaunay:

Cette triangulation ne respecte pas la propriété précédente : la somme de α et γ vaut plus que 180°.

La nouvelle triangulation ne vérifie pas la condition de Delaunay : les cercles circonscrits ne sont pas vides.

Le basculement d'arête produit une triangulation de Delaunay.