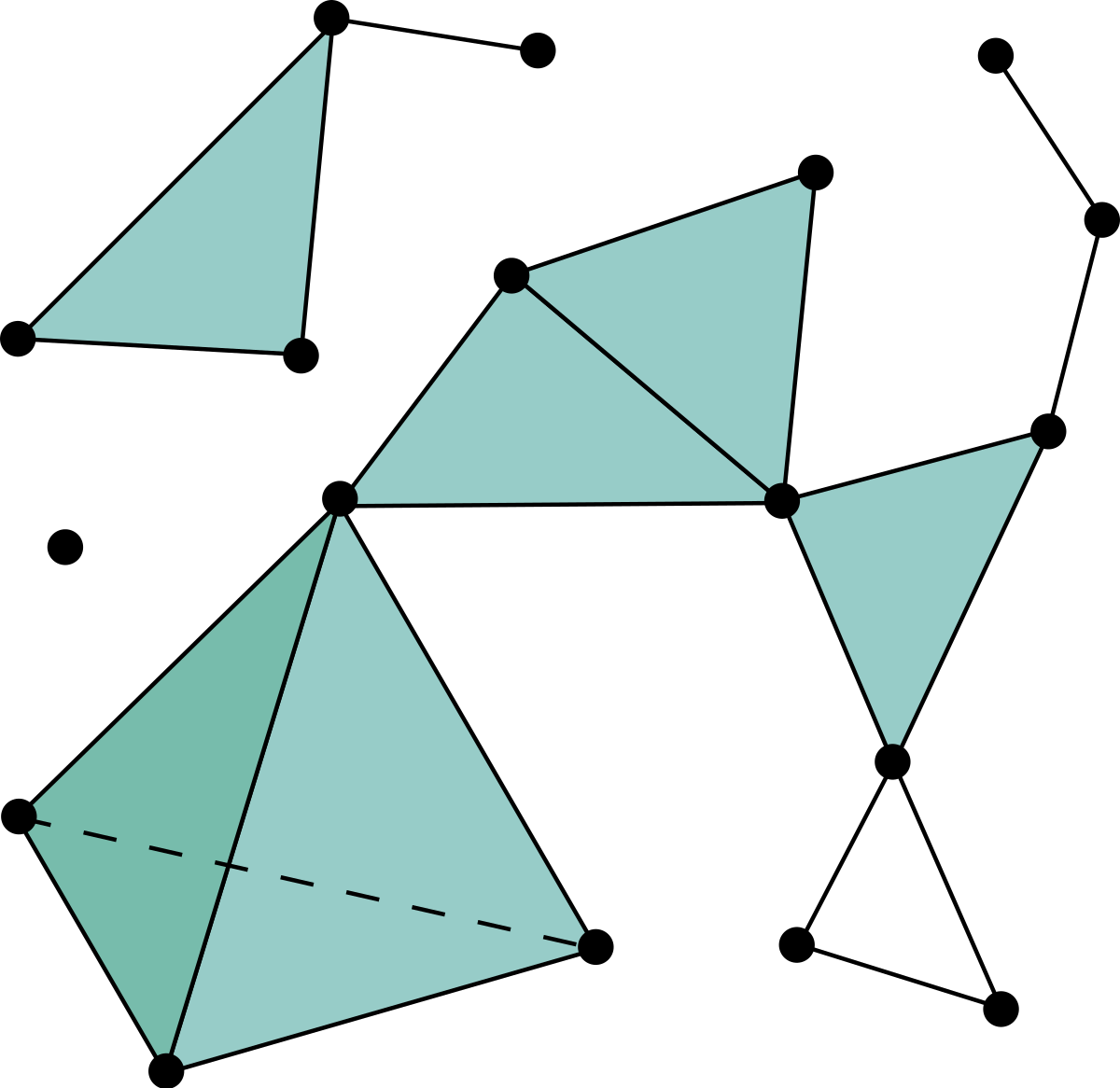
Complexe simplicial - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Approche géométrique - Δ-complexe - Approche combinatoire - Homologie simpliciale - Exemples - Résultats généraux. - Calculs effectifs

Introduction

Représentation d'un complexe simplicial.

En mathématiques, un complexe simplicial est un objet géométrique déterminé par une donnée combinatoire et permettant de décrire certains espaces topologiques en généralisant la notion de triangulation d'une surface. Un tel objet se présente comme un graphe avec des sommets reliés par des arêtes, sur lesquelles peuvent se rattacher des faces triangulaires, elles-mêmes bordant éventuellement des faces de dimension supérieure…

Cette structure est particulièrement utile en topologie algébrique, car elle facilite le calcul des groupes d'homologie de certains espaces comme les polyèdres et certaines variétés topologiques qui admettent une décomposition en complexe simplicial.

La structure de complexe simplicial est enrichie dans celle d'ensemble simplicial, puis généralisée par celle de CW-complexe en autorisant des rattachements de faces non combinatoires.

Approche géométrique

Définition

La définition de complexe simplicial géométrique fait appel à celle de simplexe affine. Dans un espace affine réel, un simplexe est défini comme l'enveloppe convexe d'un ensemble fini de points dont aucun ne peut être obtenu comme barycentre des autres. Ces points sont appelés les sommets du simplexe. L'ensemble des sommets peut être déduit du simplexe comme étant l'ensemble de ses points extrémaux. Par exemple, un triangle ou un tétraèdre sont des simplexes, ayant respectivement 3 et 4 sommets. Un segment est aussi un simplexe dont les deux sommets sont ses extrémités.

Les faces d'un simplexe sont les enveloppes convexes des sous-ensembles des sommets. Le terme « face » comprend donc ici les sommets (singletons), les arêtes, les faces triangulaires et ainsi de suite en dimension supérieure.

Un complexe simplicial géométrique est un ensemble $K$ de simplexes d'un espace affine tel que :

Toutes les faces de chaque simplexe de $K$ appartiennent aussi à $K$ ;
L'intersection de deux simplexes non disjoints doit exactement être une de leurs faces communes. Elle est l'enveloppe convexe de leurs sommets communs.

L'exemple le plus simple d'un complexe simplicial est l'ensemble des faces d'un simplexe. Ainsi, un triangle est composé de trois sommets, trois côtés et une surface intérieure. Dans l'espace, un tétraèdre est composé de quatre sommets, de six arêtes, de quatre faces triangulaires et d'un volume intérieur.

Polyèdre et triangulation

Le polyèdre associé à un complexe simplicial géométrique $K$ est simplement la réunion de tous les simplexes qu'il contient. Il est noté $| K |$ . La donnée d'un complexe simplicial et d'un homéomorphisme entre son polyèdre et un espace topologique $X$ constitue une triangulation de $X$ .

Ainsi un cube ne se présente pas naturellement comme un complexe simplicial, notamment parce que ses faces ne sont pas triangulaires, mais il admet plusieurs triangulations possibles.

Application simpliciale

Une application simpliciale entre deux complexes simpliciaux est une application continue entre leurs polyèdres qui associe aux sommets de chaque simplexe des sommets d'un même simplexe (sans être nécessairement injective) et dont la restriction à chaque simplexe est affine. Une telle application est donc complètement déterminée par les images des sommets.

Ces applications simpliciales permettent d'approcher n'importe quelle application continue entre deux espaces triangulés.

Δ-complexe

Les $Δ$ -complexes généralisent les complexes simpliciaux avec une construction similaire à celle des CW-complexes.

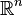
On appelle simplexe standard $Δ n$ de dimension n l'enveloppe convexe dans $\mathbb R^n$ des points $e 0$ , $e 1$ , ..., $e n$ , où $e 0 = (0,...,0)$ et où $e i = (0...,0,1,0,...,0)$ , le 1 étant placé à la i-ème position. L'ordre des sommets du simplexe standard a ici une importance capitale : non seulement, il oriente le simplexe lui-même mais en plus, il fournit automatiquement une orientation automatique de toutes les faces ; Le signe de l'orientation intervient dans la définition du bord ci-dessous.

Pour définir un $Δ$ -complexe, on commence par prendre la réunion disjointe d'une famille de simplexes standards disjoints (de dimension variable) . On quotiente alors l'espace topologique obtenu par une relation d'équivalence que l'on définit de la façon suivante : On choisit arbitrairement une collection de familles de faces de même dimension (une dimension par famille de faces), chaque face faisant partie de l'un des simplexes dont on vient de faire la réunion disjointe (rien n'empeche de prendre plusieurs face du même simplexe). On identifie alors toutes les faces de chaque famille par en utilisant les applications linéaires préservant l'ordre des sommets. Notez qu'un effet collatéral est l'identification de certains sommets.

Les $Δ$ -complexes peuvent sembler plus généraux que les complexes simpliciaux mais en fait tout $Δ$ -complexe est homéomorphe à un complexe simplicial. Il suffit en effet d'effectuer deux subdivisions barycentrique successives pour transformer un $Δ$ -complexe en complexe simplicial.