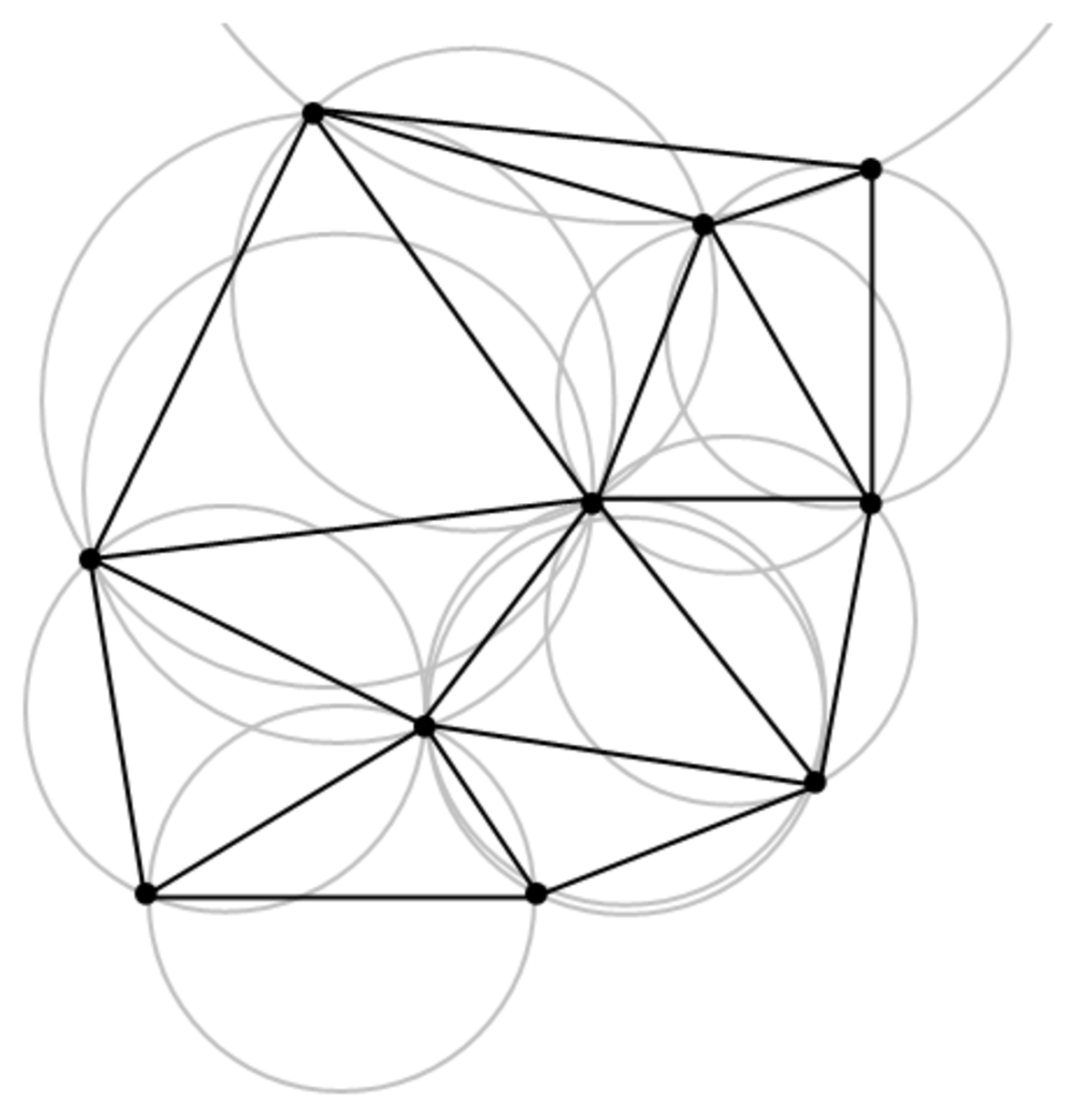
Triangulation de Delaunay - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques et plus particulièrement en géométrie algorithmique, la triangulation de Delaunay d'un ensemble P de points du plan est une triangulation DT(P) telle qu'aucun point de P n'est à l'intérieur du cercle circonscrit d'un des triangles de DT(P). Les triangulations de Delaunay maximisent le plus petit angle de l'ensemble des angles des triangles, évitant ainsi les triangles « allongés ». Cette triangulation a été inventée par le mathématicien russe Boris Delaunay (1890 - 1980) en 1934.
D'après la définition de Delaunay, le cercle circonscrit d'un triangle constitué de trois points de l'ensemble de départ est vide s'il ne contient pas d'autres sommets que les siens. Ainsi, les autres points sont autorisés sur le périmètre en lui-même mais pas à l'intérieur strict du triangle.
La condition de Delaunay affirme qu'un réseau de triangles est une triangulation de Delaunay si tous les cercles circonscrits des triangles du réseau sont vides. Ceci constitue la définition originale en deux dimensions. En remplaçant les cercles par des sphères circonscrites, il est possible d'étendre la définition à la dimension trois.
Il n'existe pas de triangulation de Delaunay pour un ensemble de points alignés. De toute manière, la triangulation n'est dans ce cas pas définie.
Pour 4 points cocycliques, tels que les sommets d'un rectangle, la triangulation de Delaunay n'est pas unique. Trivialement, les triangulations utilisant chacune des deux diagonales satisfont la condition de Delaunay.
Il est possible de généraliser cette notion pour des mesures non euclidiennes, sans garantie de l'existence ou de l'unicité de la triangulation.
Relation avec les diagrammes de Voronoï

La triangulation de Delaunay d'un ensemble discret P de points est le graphe dual du diagramme de Voronoï associé à P. A chaque cellule du diagramme de Voronoï est associé un sommet dans la triangulation de Delaunay. Ces sommets sont reliés entre eux par une arête si les cellules sont voisines. Les arêtes du diagramme de Voronoï sont sur les médiatrices des arêtes de la triangulation de Delaunay.
Propriétés
Soient n le nombre de points et d le nombre de dimensions.
- L'union de tous les simplexes d'une triangulation constitue l'enveloppe convexe des points.
- La triangulation de Delaunay contient au plus
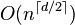
- Dans le plan, c'est-à-dire pour d=2, s'il y a b sommets dans l'enveloppe convexe, alors toute triangulation a au plus 2b - 2 - b triangles, plus un sur la face extérieure (voir la caractéristique d'Euler).
- Dans le plan, chaque sommet est en moyenne entouré de six triangles.
- Si un cercle passant par deux des points de l'ensemble n'en contient aucun autre dans son intérieur, alors le segment reliant les deux points est un segment de la triangulation de cet ensemble.
- La triangulation de Delaunay d'un ensemble de points dans un espace de dimension d est la projection de l'enveloppe convexe des projections des points sur une paraboloïde de dimension d+1.
En dimension quelconque
Pour un ensemble P de points dans l'espace Euclidien en n dimensions, une triangulation de Delaunay est une triangulation DT(P) telle qu'aucun point de P ne se trouve dans l'hypersphère circonscrite d'un simplexe de DT(P).
Une triangulation de Delaunay dans le plan est unique si les points sont dans une position générale, c'est-à-dire en dimension 2 s'il n'y a pas trois points alignés ou quatre points cocycliques et, en dimension d, il suffit qu'il n'y ait pas d + 1 points dans le même hyperplan et d + 2 sur la même hypersphère.
Le problème de la construction de la triangulation de Delaunay d'un ensemble de points en dimension n dans un espace euclidien peut être ramené au problème de la construction de l'enveloppe convexe d'un ensemble de points en dimension n + 1. Pour ce faire, on attribue à chaque point p une coordonnée supplémentaire, que l'on fixe à | p | 2, on prend le fond de l'enveloppe convexe et on retourne en dimension n en supprimant la dernière coordonnée. Comme l'enveloppe convexe est unique, la triangulation l'est aussi tant que toutes les faces de l'enveloppe convexe sont des simplexes. Si une face n'est pas un simplexe, cela signifie que n + 2 points se trouvent sur la même hypersphère et donc que les points ne sont pas en position générale.