Dimension de Krull - Définition

Introduction

En mathématiques, et plus particulièrement en géométrie algébrique, la taille et la complexité d'une variété algébrique (ou d'un schéma) est d'abord mesurée sa dimension. Elle est basée sur la topologie de Zariski et coïncide avec l'intuition dans le cas des espaces affines.

Espaces irréductibles

Soit X un espace topologique. On dit que X est irréductible si tout ouvert non-vide de X est partout dense dans X. Cela revient à dire que si Y et Z sont deux parties fermées dont la réunion est égale à X, alors l'une d'entre elles est égale à X.

Une partie de X est dite irréductible si elle est irréductible pour la topologie induite.

Dans un espace irréductible, tout ouvert non-vide est dense.

Un point η d'un espace topologique est appelé un point générique si son adhérence est égale à X tout entier. Si un point générique existe, X est irréductible. Inversement, pour l'espace topologique sous-jacent à un schéma, il est irréductible si et seulement s'il admet un point générique. Celui-ci est alors unique.

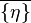
Exemples:

• Un singleton est irréductible. Un espace topologique séparé est irréductible si et seulement s'il est réduit à un point.

• Le spectre d'un anneau commutatif unitaire Spec A est irréductible si A est un anneau intègre. Le point correspondant à l'idéal nul est le point générique.

Dimension de Krull

Une chaîne de longueur n dans X est une suite strictement croissante

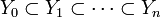
de n + 1 parties fermées irréductibles de X. La dimension de Krull de X est le supremum (éventuellement infini) des longueurs des chaînes dans X. L'ensemble vide est de dimension par convention. La dimension de X est le supremum des dimensions de ses composantes irréductibles.

Exemples:

• Un espace topologique discret est de dimension 0.

• Un espace non-vide est irréductible de dimension 0 si et seulement si les seuls ouverts sont l'ensemble vide et l'espace tout entier.

• La droite affine Spec K[T] sur un corps K, munie de sa topologie de Zariski, est de dimension 1. En effet, ses parties fermées sont les parties finies et l'espace lui-même. Les parties fermées finies irréductibles sont les points fermés. Ainsi, toute chaîne de longueur maximale est constituée d'un point fermé et de l'espace tout entier. Donc la dimension de Krull est 1. Plus généralement, l'espace affine Spec est de dimension n.

• Si on considère une hypersurface V(f) dans Spec avec non constant, alors elle est de dimension n − 1. En particulier, si n = 2, on obtient une courbe plane sur K.

• ℝⁿ muni de sa topologie usuelle est de dimension de Krull nulle, quel que soit l'entier n. En effet les seuls fermés irréductibles de ℝⁿ sont les singletons. La dimension de Krull n'est donc pas pertinente pour la topologie usuelle, elle s'utilise plutôt avec la topologie de Zariski sur les variétés algébriques.

Remarque Pour un schéma noethérien X, la dimension de Krull peut être déterminée de façon similaire à la dimension topologique.

Composantes irréductibles

Une composante irréductible de X est une partie (nécessairement fermée) de X irréductible et qui n'est strictement contenue dans aucune autre partie irréductible de X.

Le lemme de Zorn implique que tout point x appartient à une composante irréductible (la partie {x} est irréductible, et on considère l'ensemble des parties irréductibles contenant x). Ainsi X est la réunion de ses composantes irréductibles.

Dans le cas des variétés algébriques ou plus généralement des schémas noethériens, les composantes irréductibles sont en nombre fini. De plus, si un espace topologique X ayant cette propriété de finitude est recouvert par un nombre fini de parties fermées irréductibles sans relation d'inclusion entre elles, alors ces parties fermées sont exactement les composantes irréductibles de X. Pour l'ensemble des nombres réels avec la topologie usuelle, tout point est une composante irréductible.