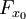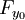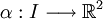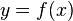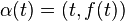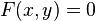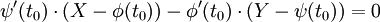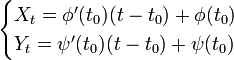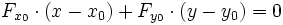Courbe plane - Définition

Introduction

En géométrie, une courbe plane est une courbe qui est entièrement contenue dans un (unique) plan, et qui est identifiable à une fonction continue :

où I est un intervalle de l'ensemble des nombres réels.

L'image d'une courbe est aussi appelée support de la courbe. Parfois, on utilise aussi l'expression courbe pour indiquer le support d'une courbe. Une courbe sur un espace euclidien de dimension supérieure à 2 est dite plane si son support est contenu dans un plan lui-même contenu dans l'espace euclidien dans lequel elle est définie.

Une courbe plane est dite simple si elle ne se recoupe pas, autrement dit, si

.

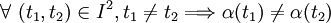
Représentations

Représentation par une forme cartésienne explicite

Une manière de représenter une courbe plane est l'équation :

telle qu'à chaque point x corresponde un point y, et de façon à ce que chaque point du plan xy : (x,y) représente le support de la courbe. Une courbe de ce type est également nommée graphique en référence au graphique d'une fonction réelle ; en effet, la représentation peut aussi s'écrire :

c'est-à-dire comme fonction d'une variable indépendante. Cette représentation a de nombreuses limites géométriques, du fait que très souvent, une courbe a une description très complexe sous cette forme, qui n'est donc pas adaptée à l'étude des propriétés géométriques.

Représentation par une forme cartésienne implicite

Une courbe peut également être représentée sous la forme :

c'est-à-dire comme fonction de deux variables indépendantes. Cette représentation est, selon certains points de vue, meilleure que la représentation explicite ; cependant, on peut rencontrer des problèmes quand il faut expliciter l'une des deux variables en fonction de l'autre : souvent, c'est très compliqué, quand ce n'est pas impossible.

Représentation paramétrée

La meilleure représentation est sans aucun doute la représentation paramétrée, du type :

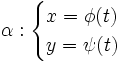
ou bien α(t) = (φ(t),ψ(t))

où s'appelle le paramètre.

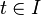
La condition de continuité ne suffit pas pour représenter et étudier les courbes vues comme objets filiformes à une dimension avec les caractéristiques de régularité voulues. La condition supplémentaire est que la courbe plane soit différentiable sur I.

Une courbe plane paramétrée α(t) = (φ(t),ψ(t)) est dite différentiable en tout point si les fonctions φ(t) et ψ(t) ont des dérivées continues en tout point.

On dit qu'une courbe plane paramétrée est régulière en un point t₀ (ou que t₀ est un point régulier pour cette courbe) si  ; elle est dite régulière sur I si en tout point t de I.

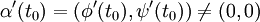
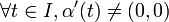
Un point t₀ tel que α'(t₀) = (0,0) est appelé point singulier pour la courbe.

Normale

La régularité de la courbe permet de définir la droite normale à la courbe au point t₀, d'équation cartésienne :

.

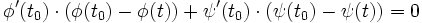
Cette équation devient, avec les mêmes notations que dans le paragraphe précédent :

• Pour une représentation explicite :

.

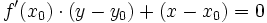
• Pour une représentation implicite :

.

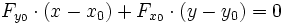
Tangente

La régularité de la courbe permet de définir la droite tangente à la courbe. Soient α(t) une courbe différentiable et P₀ = α(t₀) un point régulier. On peut définir la tangente à la courbe en ce point comme étant la droite passant par P₀ et parallèle au vecteur α'(t₀) = (φ'(t₀),ψ'(t₀)).

La tangente a une équation cartésienne au point t₀ :

et pour équations paramétrées :

Dans le cas d'une courbe représentée explicitement par une équation y = f(x), la tangente au point (x₀,y₀) est donnée par la relation :

.

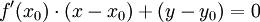
Dans le cas d'une courbe représentée par une équation implicite F(x,y) = 0, la tangente au point (x₀,y₀) est donnée par la relation :

où (respectivement ) désigne la dérivée partielle par rapport à x (respectivement y) de F, évaluée au point x₀ (respectivement y₀).